SVM 是一个非常优雅的算法,具有完善的数学理论,虽然如今工业界用到的不多,但还是决定花点时间去写篇文章整理一下。
1. 支持向量
1.1 线性可分
首先我们先来了解下什么是线性可分。

在二维空间上,两类点被一条直线完全分开叫做线性可分。
严格的数学定义是:
和
是 n 维欧氏空间中的两个点集。如果存在 n 维向量 w 和实数 b,使得所有属于
的点
都有
,而对于所有属于
的点
则有
,则我们称
和
线性可分。
1.2 最大间隔超平面
从二维扩展到多维空间中时,将 和
完全正确地划分开的
就成了一个超平面。
为了使这个超平面更具鲁棒性,我们会去找最佳超平面,以最大间隔把两类样本分开的超平面,也称之为最大间隔超平面。
- 两类样本分别分割在该超平面的两侧;
- 两侧距离超平面最近的样本点到超平面的距离被最大化了。
1.3 支持向量
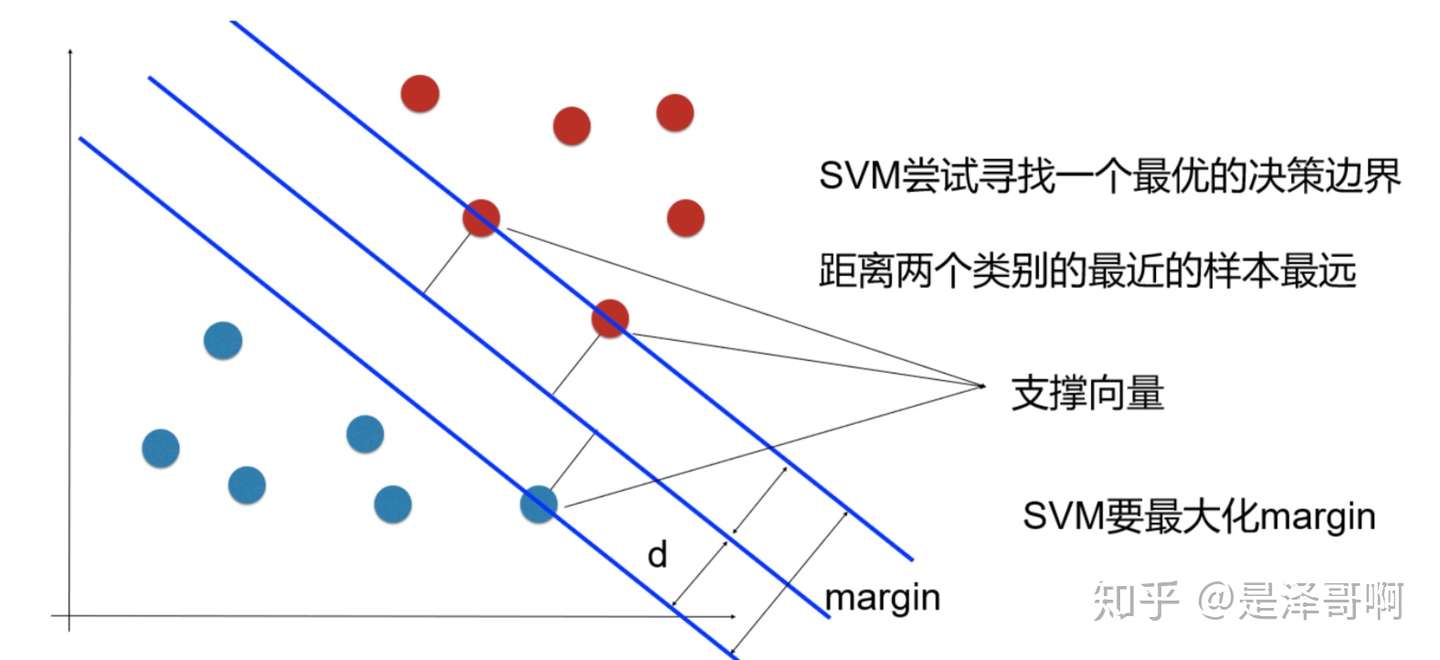
样本中距离超平面最近的一些点,这些点叫做支持向量。
1.4 SVM 最优化问题
SVM 想要的就是找到各类样本点到超平面的距离最远,也就是找到最大间隔超平面。任意超平面可以用下面这个线性方程来描述:
二维空间点 到直线
的距离公式是:
扩展到 n 维空间后,点 到直线
的距离为:
其中 。
如图所示,根据支持向量的定义我们知道,支持向量到超平面的距离为 d,其他点到超平面的距离大于 d。
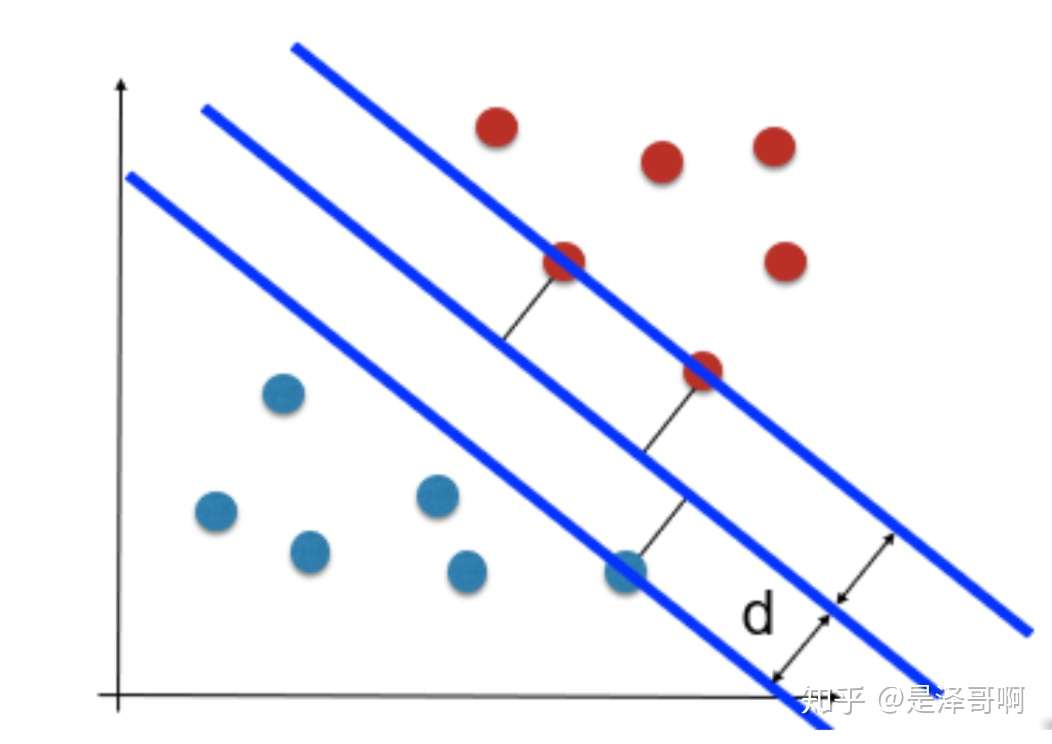
于是我们有这样的一个公式:
稍作转化可以得到:
是正数,我们暂且令它为 1(之所以令它等于 1,是为了方便推导和优化,且这样做对目标函数的优化没有影响),故:
将两个方程合并,我们可以简写为:
至此我们就可以得到最大间隔超平面的上下两个超平面:
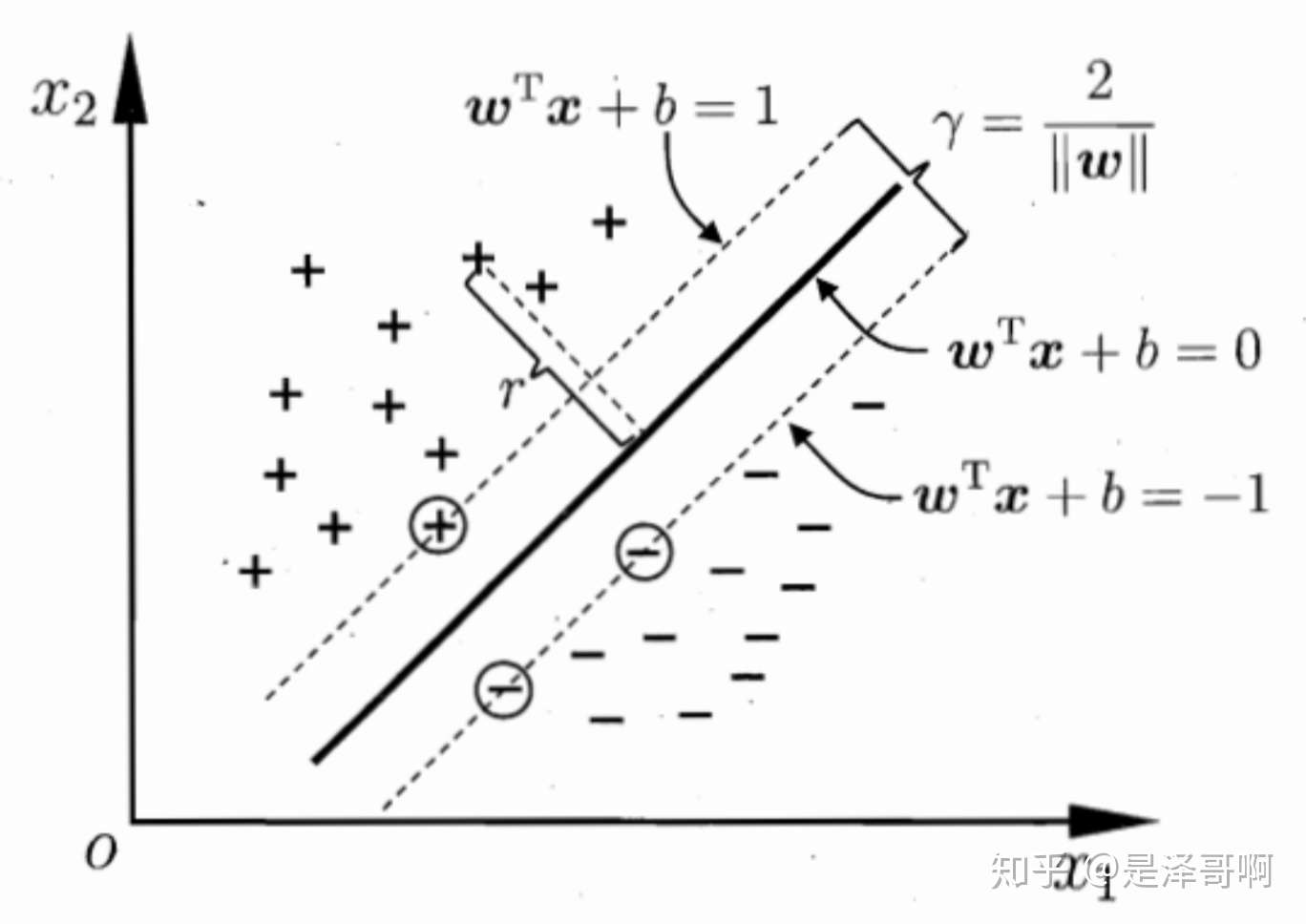
每个支持向量到超平面的距离可以写为:
由上述 可以得到
,所以我们得到:
最大化这个距离:
这里乘上 2 倍也是为了后面推导,对目标函数没有影响。刚刚我们得到支持向量 ,所以我们得到:
再做一个转换:
为了方便计算(去除 的根号),我们有:
所以得到的最优化问题是:
2. 对偶问题
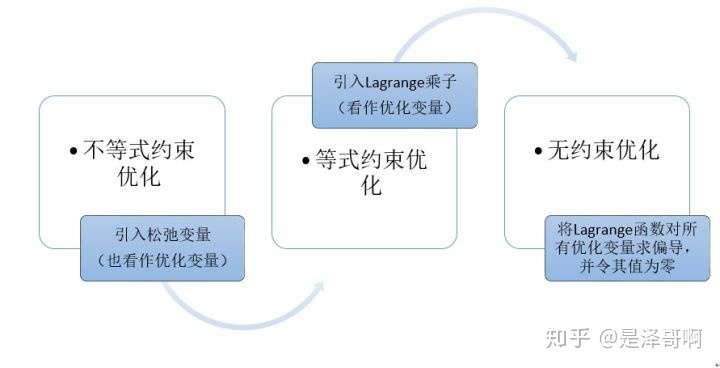
2.1 拉格朗日乘数法
2.1.1 等式约束优化问题
本科高等数学学的拉格朗日程数法是等式约束优化问题:
我们令 ,函数
称为 Lagrange 函数,参数
称为 Lagrange 乘子没有非负要求。
利用必要条件找到可能的极值点:
具体是否为极值点需根据问题本身的具体情况检验。这个方程组称为等式约束的极值必要条件。
等式约束下的 Lagrange 乘数法引入了 个 Lagrange 乘子,我们将
与
一视同仁,把
也看作优化变量,共有
个优化变量。
2.1.2 不等式约束优化问题
而我们现在面对的是不等式优化问题,针对这种情况其主要思想是将不等式约束条件转变为等式约束条件,引入松弛变量,将松弛变量也是为优化变量。
以我们的例子为例:
我们引入松弛变量 得到
。这里加平方主要为了不再引入新的约束条件,如果只引入
那我们必须要保证
才能保证
,这不符合我们的意愿。
由此我们将不等式约束转化为了等式约束,并得到 Lagrange 函数:
由等式约束优化问题极值的必要条件对其求解,联立方程:
(为什么取 ,可以通过几何性质来解释,有兴趣的同学可以查下 KKT 的证明)。
针对 我们有两种情况:
情形一:
由于 ,因此约束条件
不起作用,且
情形二:
此时 且
,可以理解为约束条件
起作用了,且
综合可得: ,且在约束条件起作用时
;约束不起作用时
由此方程组转换为:
以上便是不等式约束优化优化问题的 KKT(Karush-Kuhn-Tucker) 条件, 称为 KKT 乘子。
这个式子告诉了我们什么事情呢?
直观来讲就是,支持向量 ,所以
即可。而其他向量
。
我们原本问题时要求: ,即求
由于 ,故我们将问题转换为:
:
假设找到了最佳参数是的目标函数取得了最小值 p。即 。而根据
,可知
,因此
,为了找到最优的参数
,使得
接近 p,故问题转换为出
。
故我们的最优化问题转换为:
出了上面的理解方式,我们还可以有另一种理解方式: 由于 ,
所以 ,所以转化后的式子和原来的式子也是一样的。
更多内容,可以看这个大佬的介绍,超详细。https://zhuanlan.zhihu.com/p/77750026