多项式与快速傅里叶变换

记录重要的，有利于理解的部分

多项式的表示

系数表达

对一个次数界(degree bound)为n的多项式$A(x)={\sum }_{j=0}^{n-1}{a}_j{x}^j$而言，其系数表达是一个由系数组成的向量
$$a=(a_0,a_1,...,a_{n-1})$$

• 求值运算

  • 霍纳法则：时间复杂度 $O(N)$

• 乘法运算

  • 卷积(convolution)：$c=a\otimes b$

    时间复杂度：$O(N)$

点值表达

一个表达式可以有很多不同的点值表达，采取n个不同的点$x_0,x_1,...,x_n$构成的集合
$$\{(x_0,y_0),(x_1,y_1),...,(x_{n-1},y_{n-1})\}$$
其中，
$$y_k=A(x_k)$$

• 插值运算：求值运算的逆，从一个多项式的点值表达确定其系数表达形式。

  • 插值多项式具有唯一性

  • 解法一：列出范德蒙德矩阵，利用LU分解算法，求解时间复杂度$O(n^3)$

  • 解法二：基于拉格朗日公式，求解时间复杂度$O(n^2)$

    $$A(x)=\sum _{k=0}^{n-1}{y}_k\frac{{\prod }_{j\ne k}(x-x_j)}{{\prod }_{j\ne k}(x_k-x_j)}$$

系数形式表示的多项式的快速乘法

我们可以采用任何点作为求值点，但通过精心地挑选求值点，可以把两种表示法之间转化所需的时间复杂度变为$O(nlgn)$。

• DFT：离散傅里叶变换
• 逆DFT

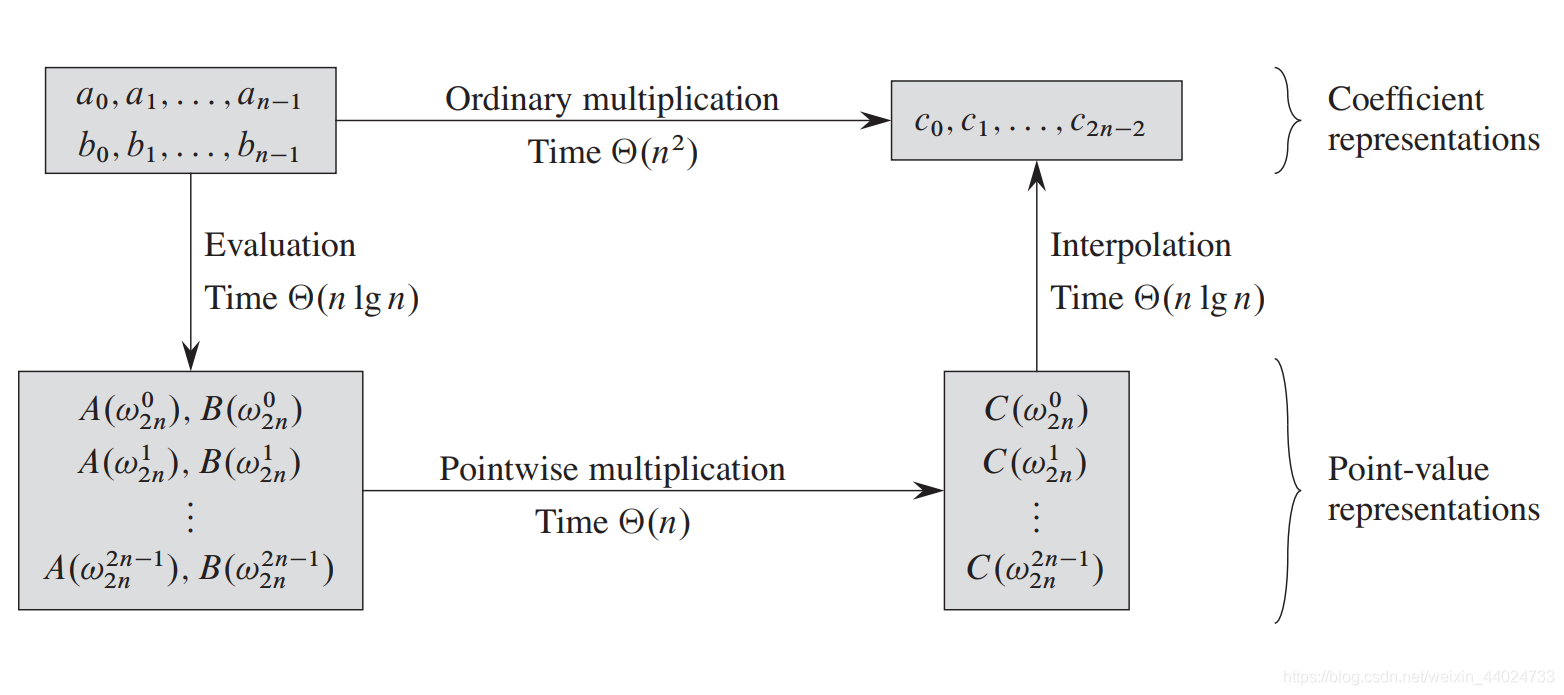
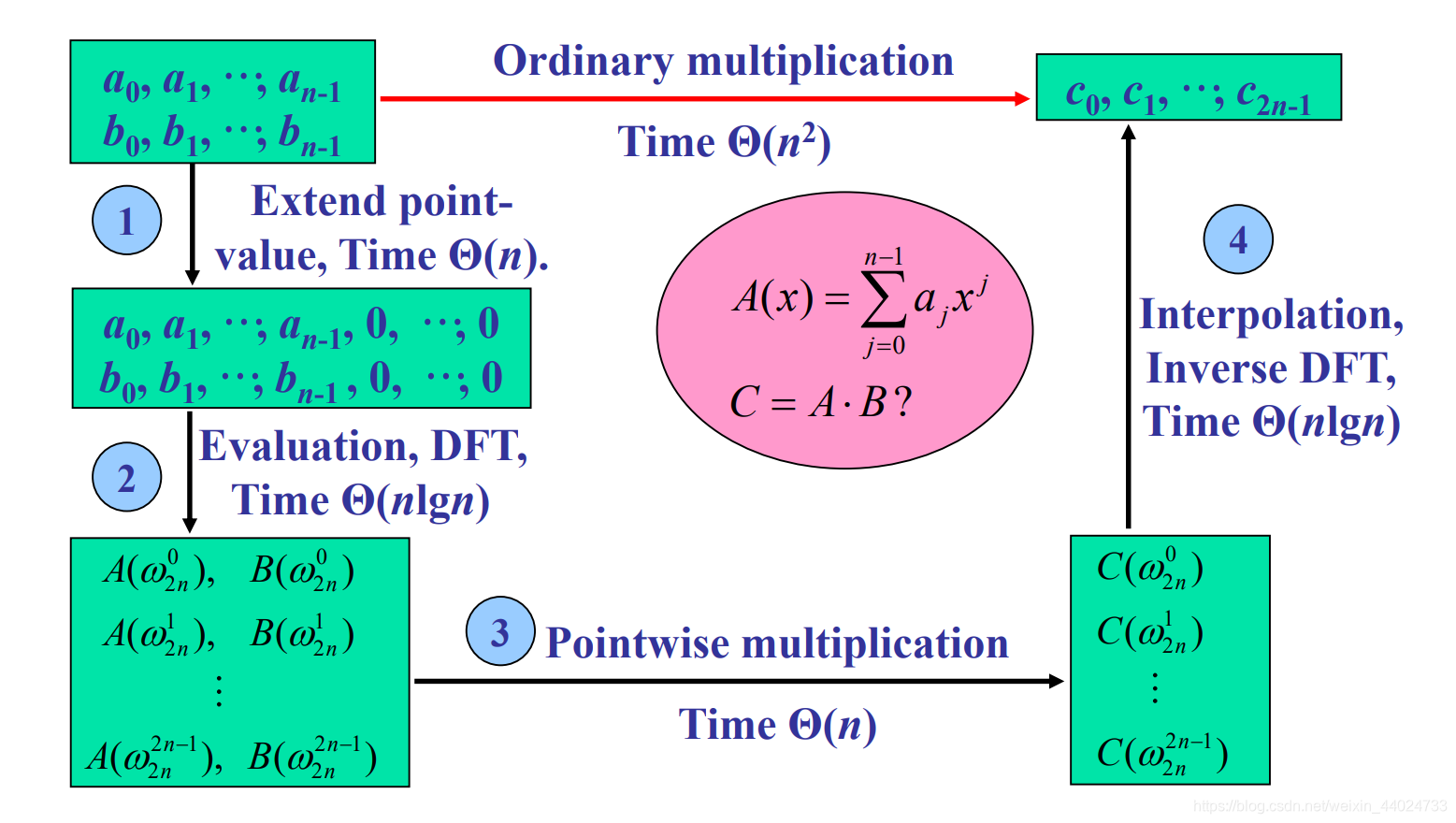
细节：两个次数界为n的多项式乘积是一个次数界为2n的多项式，因此，在对输入多项式A和B进行求值以前，首先把这两个多项式在高次系数前添加n个0，使其次数界加倍为2n。因为现在这些向量有2n个元素，我们可以采用 “2n次单位复数根” ，记为 ${\omega }_{2n}$。

过程：

1. 加倍次数界
2. 求值（通过应用2n阶的FFT计算出A(x)和B(x)的长度为2n的点值表达）
3. 逐点相乘
4. 插值（通过对2n个点值对应用FFT，计算其逆DFT）

DFT与FFT

上一节提到通过采用“2n次单位复数根”点可以将时间复杂度降低到$O(nlgn)$。

单位复数根

n次单位复数根是满足${\omega }^n=1$的复数$\omega$。n次单位复数根恰好有n个：对于$k=0,1,...,n-1$，这些根分别是是${\omega }^{2\pi ik/n}$。

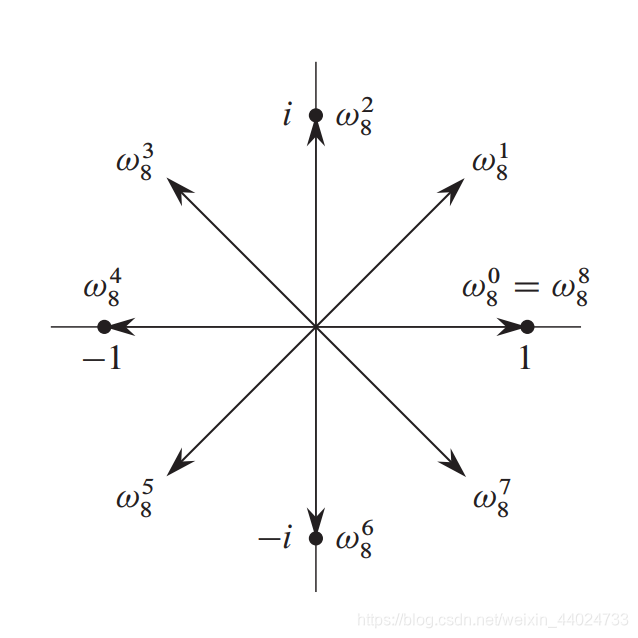
n个单位复数根均匀地分布在以复平面的原点为圆心的单位半径圆周上。值${\omega }_n=e^{2\pi i/n}$称为主n次单位根，所有其他n次复数单位根都是${\omega }_n$的幂次（0次，1次，…，n-1次，n次；其中 ${\omega }_n^0={\omega }_n^n$）。

• 引理30.3（消去引理）：对任何整数$n\ge 0,k\ge 0,d>0,$
  $${\omega }_{dn}^{dk}={\omega }_n^k$$
  感觉作用就是可以成比例变化。

$${\omega }_n^{n/2}={\omega }_2=-1$$

• 引理30.5（折半定理）：如果 $n>0$ 为偶数，那么n个n次单位复数根的平方的集合就是n/2个n/2次单位复数根的集合。
  $$({\omega }_n^k{)}^2={\omega }_{2(n/2)}^{2k}={\omega }_{n/2}^k,k=0,1,...,\frac{n}{2}-1$$

  $$({\omega }_n^{k+n/2}{)}^2={\omega }_n^{2k+n}={\omega }_n^{2k}{\omega }_n^n={\omega }_n^{2k}={\omega }_{n/2}^k,k=0,1,...,\frac{n}{2}-1$$

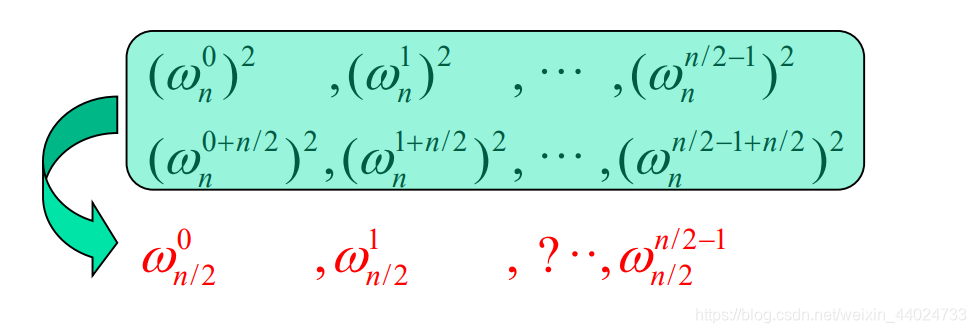
• 引理30.6（求和引理）：对任意整数$n\ge 1$和不能被n整除的非负整数k，有
  $$\sum _{j=0}^{n-1}({\omega }_n^k{)}^j=0$$

DFT

回顾一下，我们希望计算次数界为n的多项式
$$A(x)=\sum _{j=0}^{n-1}{a}_j{x}^j$$
在${\omega }_n^0,{\omega }_n^1,...,{\omega }_n^{n-1}$处的值（即在n个n次单位复数根处）。假设A以系数形式给出：$a=(a_0,a_1,...,a_{n-1})$。接下来对k=0，1，…，n-1，定义结果$y_k$
$$y_k=A({\omega }_n^k)=\sum _{j=0}^{n-1}{a}_j{\omega }_n^{kj}$$
向量 $y=(y_0,y_1,...,y_{n-1})$就是系数向量 $a=(a_0,a_1,...,a_{n-1})$ 的离散傅里叶变换（DFT）。记为$y=DF{T}_n(a)$。

FFT

通过使用一种称为**快速傅里叶变换（FFT）**的方法，利用复数单位根的特殊性质，可以在$O(nlogn)$时间内计算出$DF{T}_n(a)$。

通篇假设n恰好是2的整数幂。

FFT利用了分治策略，采用A(x)中偶数下标的系数与奇数下标的系数，分别定义两个新的次数界为n/2的多项式 $A^{[0]}(x)$ 和 $A^{[1]}(x)$：
$$A^{[0](X)}=a_0+a_{2}x+a_4{x}^2+...+a_{n-2}{x}^{n/2-1}$$

$$A^{[1](X)}=a_1+a_{3}x+a_5{x}^2+...+a_{n-1}{x}^{n/2-1}$$

于是有：
$$A(x)=A^{[0]}(x^2)+x{A}^{[1]}(x^2)$$
所以，求A(x)在${\omega }_n^1,{\omega }_n^2,...,{\omega }_n^{n-1}$处的值的问题转换为：

1. 求次数界为n/2的多项式 $A^{[0]}(x)$ 和 $A^{[1]}(x)$在点
   $$({\omega }_n^0{)}^2,({\omega }_n^1{)}^2,...,({\omega }_n^{n-1}{)}^2$$
   的取值。

2. 根据 $A(x)=A^{[0]}(x^2)+x{A}^{[1]}(x^2)$ 综合结果。

根据折半定理，式$({\omega }_n^0{)}^2,({\omega }_n^1{)}^2,...,({\omega }_n^{n-1}{)}^2$并不是由n个不同的值组成，而是由n/2个n/2次单位复数根所组成，每个根正好出现2次。

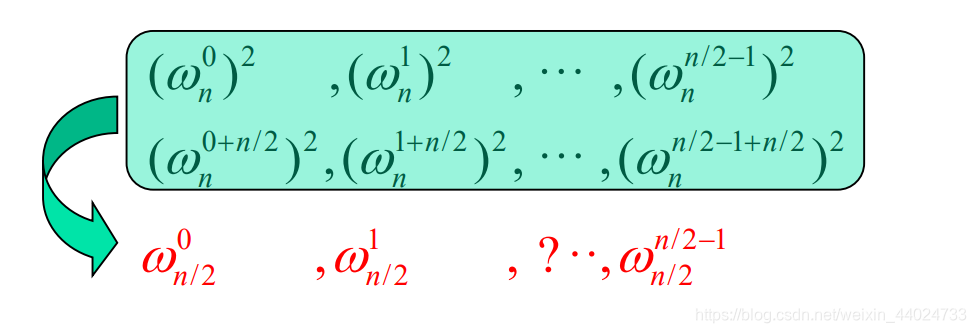
因此，可以递归地对次数界为n/2的多项式 $A^{[0]}(x)$ 和 $A^{[1]}(x)$ 在n/2个n/2次单位复数根处进行求值。这些子问题与原始问题形式相同，但规模变为一半。

现在，我们以及成功地把一个n个元素的$DF{T}_n$ 计算划分为两个规模为n/2的元素的$DF{T}_{n/2}$ 计算。

这一分解是下面递归FFT算法的基础，此算法计算出一个由n个元素组成向量 $a=(a_0,a_1,...,a_{n-1})$ 的DFT，其中，n是2的幂。

2 ~ 3行：只有一个元素的DFT就是该元素本身
$$y_0=a_0{\omega }_1^0=a_0\cdot 1=a_0$$
6 ~ 7行：定义 $A^{[0]}(x)$ 和 $A^{[1]}(x)$ 的系数向量

4、5、13行：确保 $\omega$ 的更新

8 ~ 9行：执行递归计算 $DF{T}_{n/2}$

对于k = 0,1,2,…,n/2-1,
$$\begin{gathered} y_k^{[0]}=A^{[0]}({\omega }_{n/2}^k) \\ {y}_k^{[1]}=A^{[1]}({\omega }_{n/2}^k) \end{gathered}$$
或者，根据消去引理，有${\omega }_{n/2}^k={\omega }_n^{2k}$ ，于是
$$\begin{gathered} y_k^{[0]}=A^{[0]}({\omega }_n^{2k}) \\ {y}_k^{[1]}=A^{[1]}({\omega }_n^{2k}) \end{gathered}$$
对$y_0,y_1,...,y_{n/2-1},$ 第11行推出：
$$\begin{gathered} y_k=y_k^{[0]}+{\omega }_n^k{y}_k^{[1]}=A^{[0]}({\omega }_n^{2k})+{\omega }_n^k{A}^{[1]}({\omega }_n^{2k}) \\ =A({\omega }_n^k) \\ (x={\omega }_n^k) \end{gathered}$$
对 $y_{n/2},y_{n/2+1},...,y_{n-1},$ 第12行推出:
$$\begin{gathered} y_{k+(n/2)}=y_k^{[0]}-{\omega }_n^k{y}_k^{[1]} \\ =A^{[0]}({\omega }_n^{2k})+{\omega }_n^{k+(n/2)}{A}^{[1]}({\omega }_n^{2k}) \\ =A^{[0]}({\omega }_n^{2k+n})+{\omega }_n^{k+(n/2)}{A}^{[1]}({\omega }_n^{2k+n}) \\ =A({\omega }_n^{k+(n/2)}) \\ (x={\omega }_n^{k+(n/2)}) \end{gathered}$$
其中，${\omega }_n^{k+(n/2)}=-{\omega }_n^k$ ， ${\omega }_n^{2k}={\omega }_n^{2k+n}$ ， ${\omega }_n^k$ ：旋转因子

因此，通过采用快速傅里叶变换，可以在 $O(nlgn)$ 时间内，求出次数界为n的多项式在n个n次单位复数根处的值。

在单位复数根处插值

将多项式从点值表达转换回系数表达。

可以得到：对FFT算法进行 如下修改 就可以计算出 逆DFT ：

• 把a与y互换
• 用 ${\omega }_n^{-1}$ 替换 ${\omega }_n$
• 并将计算结果的每个元素除以n

因此，也可以在 $O(nlgn)$ 时间内计算出 $DF{T}_n^{-1}$ 。

• 定理30.8（卷积定理）：对任意两个长度为n的向量a和b，其中n是2的幂，其中向量a和b用0填充，使其长度达到2n，并用” $\cdot$ “表示2个2n个元素组成向量的点乘。

$$a\otimes b=DF{T}_{2n}^{-1}(DF{T}_{2n}(a)\cdot DF{T}_{2n}(b))$$

高效FFT实现

探究两种高效的FFT实现方法。

FFT的一种迭代实现

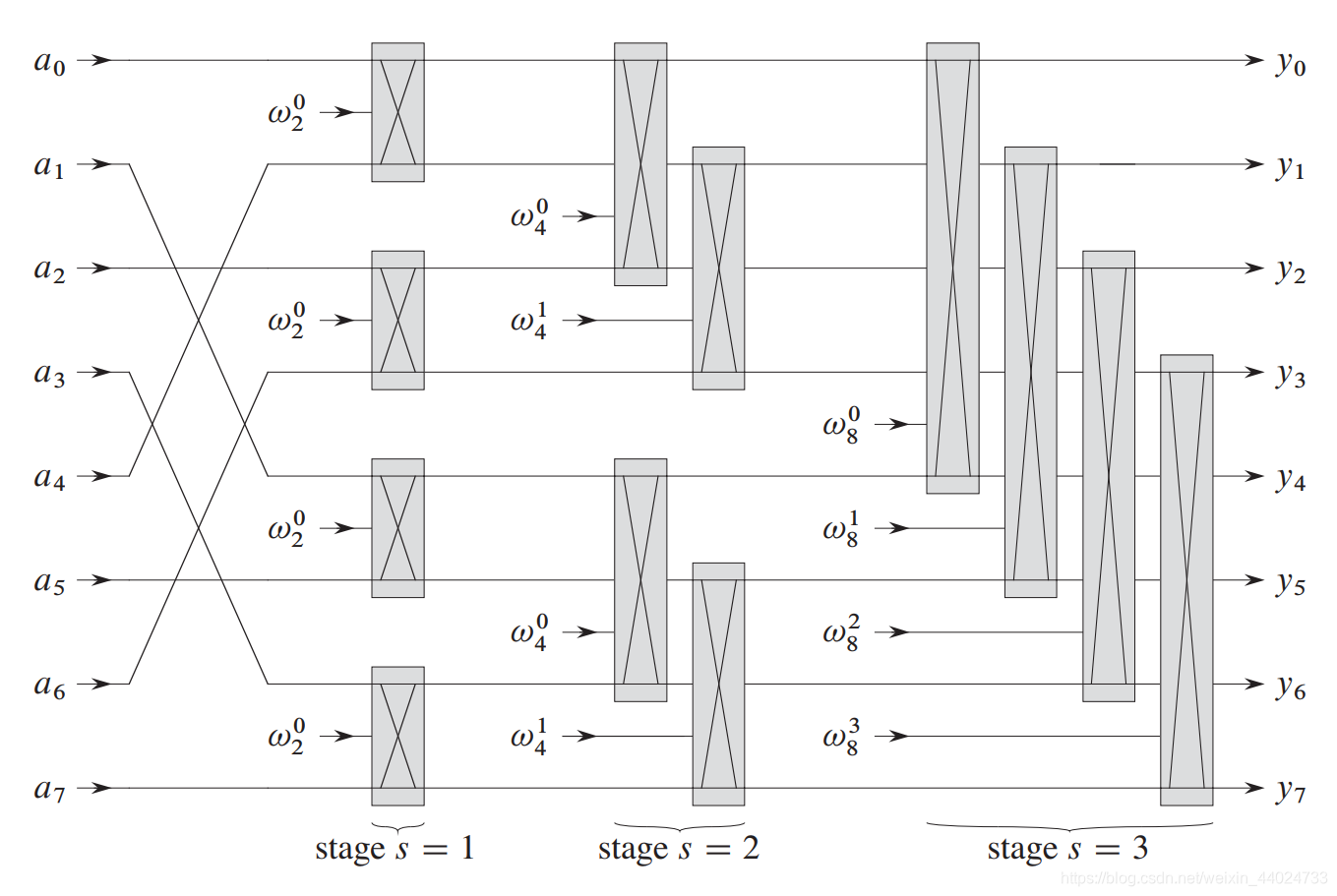
第10 ~ 13行的 for 循环中包含了 ${\omega }_n^k{y}_k^{[1]}$ 的2次计算。称该值为 公用制表达式 。可以改变循环，使其只计算一次，将其值放在临时变量 $t$ 中。

这一系列操作称为一个 蝴蝶操作 。

现在来说明如何使FFT算法采用迭代结构而不是递归结构。

树中每一个结点对应每次过程递归调用。由相应的输入向量标记。每次Recursive-FFT 调用产生两个递归调用，除非该调用已收到了1个元素的向量。第一次调用作为左孩子，第二次调用作为右孩子。

追踪过程，自底向上。

• 首先，成对取出元素，利用一次蝴蝶操作计算出每对的DFT，然后用其DFT取代这对元素。这样向量中就包含了n/2个二元素的DFT。（第四层到第三层）
• 下一步，按对取出这n/2个DFT，通过两次蝴蝶操作计算出具有四个元素向量的DFT，并用一个具有四个元素的DFT取代对应的两个二元素的DFT。于是，向量中包含n/4个四元素的DFT。
• 继续进行这一过程，直至向量包含两个具有n/2个元素的DFT，这时，综合应用n/2次蝴蝶操作，可以合成最终的具有n个元素的DFT。（第二层到第一层）

数组A[0,…,n-1]：初始时该数组包含输入向量a中的元素，其顺序为它们在上图中树叶出现的顺序（确定顺序：位逆序置换 ）。

引入变量s：计算树的层次。

更精确的伪代码：

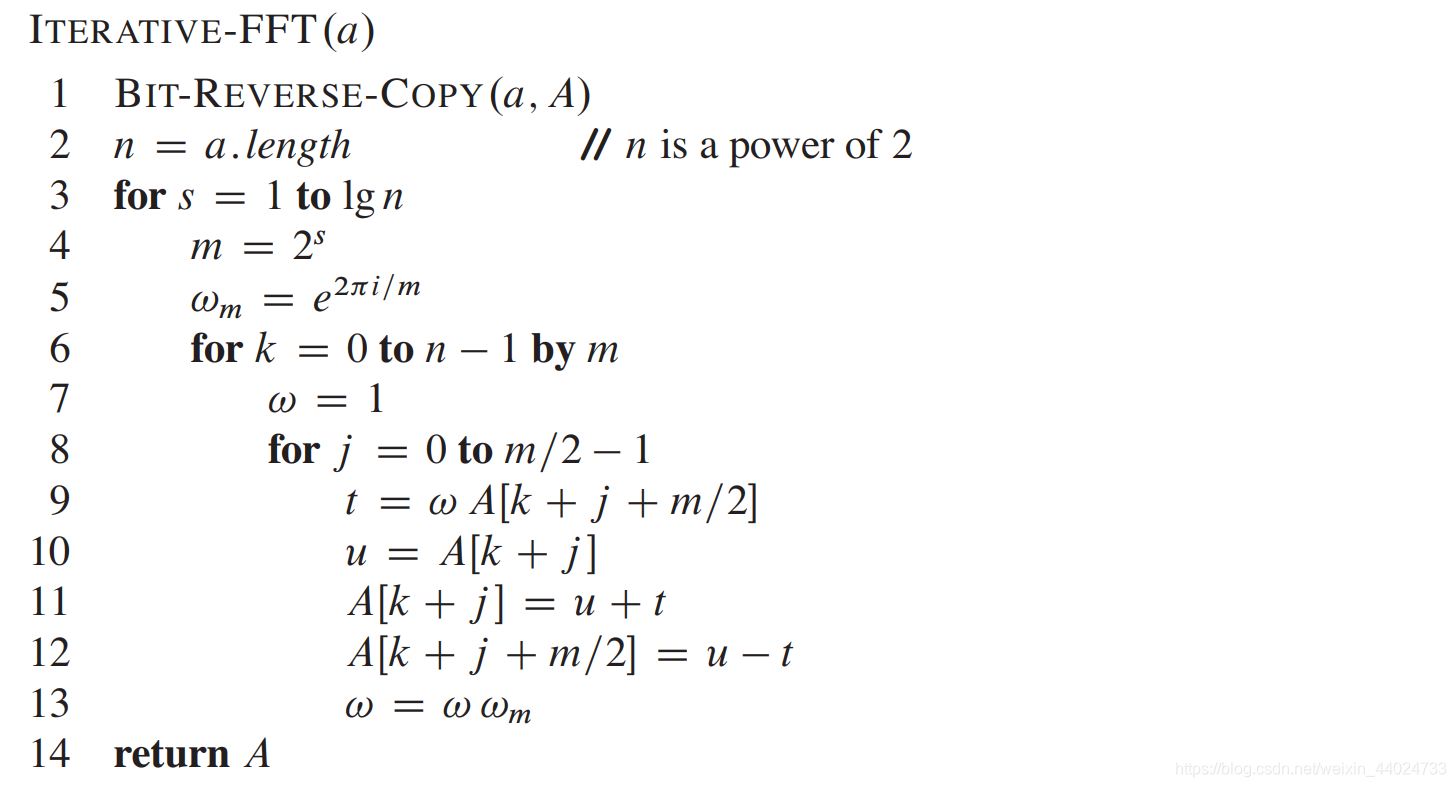
共三层循环：

1. 第一层循环：$s$ 确定所在的层数，$m=2^s$ ，要求 m个数的DFT ，${\omega }_m=e^{2\pi i/m}$ 为 $m$ 次单位复数根（通过迭代乘以 $\omega$ 得到 ${\omega }_n^k$ （k次的））。
2. 第二层循环：由于每组有m个数（k以m递增），故有n/m组。初始 ${\omega }_n^0=1$。
3. 第三层循环：蝴蝶操作 ，每组m个数，每组m/2次蝴蝶操作 （结合第二层循环：一共n/m组，共n/2次蝴蝶操作）

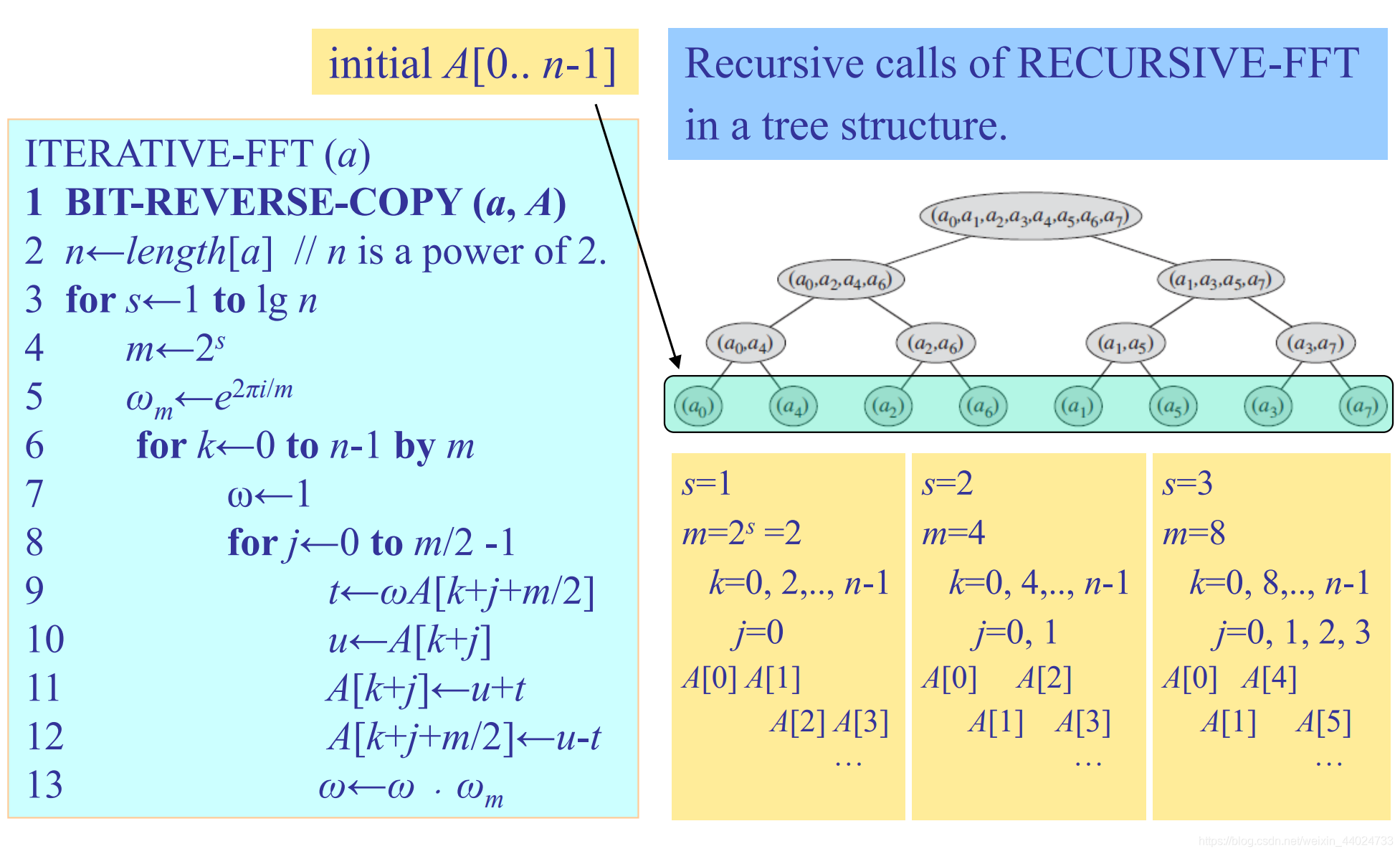
• 位逆序置换

  让 $rev(k)$ 为 $k$ 的二进制表示各位逆序所形成的 $lgn$ 位的整数，把向量中的元素 $a_k$ 放在数组的 $A[rev(k)]$ 位置上。

  例如，在上上上图中树叶出现的次序为：0，4，2，6，1，5，3，7；这个序列二进制表示为：000，100，010，110，001，101，011，111；当把二进制表示各位逆序后，得到序列：000，001，010，011，100，101，110，111（递增）。

  获得一般情况下的位逆序置换：在树的最底层，最低位为0的下标在左子树，以及最低位为1的下标在右子树中。在每一层去掉最低位后，沿着树继续这一过程，直到给出序列。

• 总体时间复杂度

  

并行FFT电路

SEE BOOK.

总结

T_T，感觉还是糊里糊涂的。

贴上FFT代码：

...