[Problem] \color{green}{\texttt{[Problem]}}[Problem]
- 给定一个 n nn 个点 m mm 条边的无向图,求出一个至少有 3 33 个点的环,使得环上的边的边权的总和最小。无解就输出
No solution.(注意,.是必须的)。 - 1 ≤ n ≤ 100 , 1 ≤ m ≤ 5 × 1 0 3 1 \leq n \leq 100,1 \leq m \leq 5 \times 10^31≤n≤100,1≤m≤5×103。
- 记 d dd 为边权的最大值,则有 1 ≤ d ≤ 1 × 1 0 5 1\leq d \leq 1 \times 10^51≤d≤1×105。
[Solution] \color{green}{\texttt{[Solution]}}[Solution]
[Part one] \color{blue}{\texttt{[Part one]}}[Part one] Floyd 的本质是什么?
对于很多人(包括一年前的笔者)而言,Floyd 算法就是:
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
这样一个 O ( n 3 ) O\left (n^3\right)O(n3) 的多源最短路算法而已。
但是为什么 Floyd 算法是对的呢?这就涉及它的核心。
原始的 Floyd 是这样的:记 f k , i , j f_{k,i,j}fk,i,j 表示从 i ii 到 j jj 且只使用 1 − k 1-k1−k 号节点作为中转点的最短路长度。什么是中转点,就是最短路径 ( i , j ) (i,j)(i,j) 上除了 i ii 和 j jj 的那些点。
于是我们有如下的转移方程:
f k , i , j = min 1 ≤ l ≤ k − 1 { f k − 1 , i , k + f k − 1 , k , j } f_{k,i,j}=\min\limits_{1 \leq l \leq k-1}\left \{f_{k-1,i,k}+f_{k-1,k,j}\right \}fk,i,j=1≤l≤k−1min{fk−1,i,k+fk−1,k,j}
它的意义是先只用 1 11 到 l ll 号节点做中转点从 i ii 走到 k kk,再只用 1 11 到 l ll 号节点做中转点从 k kk 走到 j jj。
于是我们可以用滚动数组优化它,就得到了我们上面的代码(顺便一提,正是因为我们用了滚动数组,所以 k kk 才要在最外层)。
[Part two] \color{blue}{\texttt{[Part two]}}[Part two] 回归原题
讲了这么多,它和原题有什么关系呢?
我们假设这个环上有一条边 ( i , j ) (i,j)(i,j),去除这条边后,剩下的一定是从 i ii 到 j jj 的最短路,如图:
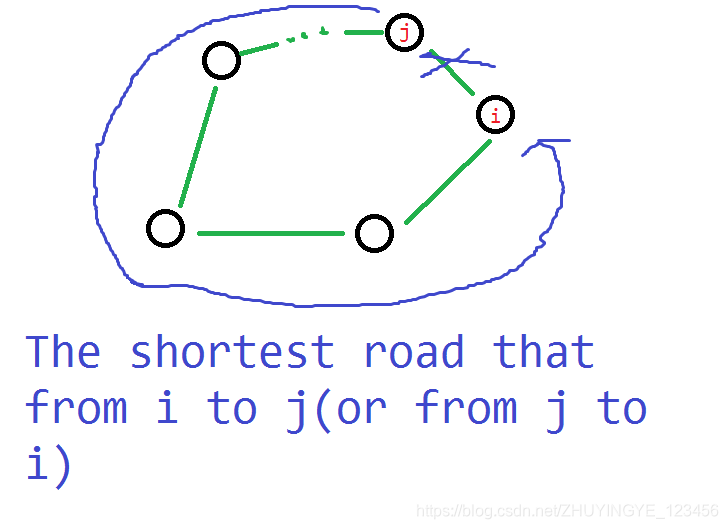
有什么用?我们随便找两个点 i ii 和 j jj,求出它们在只使用 1 11 到 k − 1 k-1k−1 号点作为中转点时的最短路 T i , j , k − 1 T_{i,j,k-1}Ti,j,k−1(f ff 实在出现了太多次了,所以为了让读者明白究竟方式了什么,这里换一个字母),连接点 i ii 和 k kk,在连接点 k kk 和 j jj,就可以得到一个环。
所以,最小的环的权值(就是换上所有边的权值总和)ans \texttt{ans}ans 的推导式为:
ans = min i , j , k ∈ { 1.. n } { T k − 1 , i , j + a i , k + a k , j } \texttt{ans}=\min\limits_{i,j,k \in \left \{ 1..n \right \} } \left \{ T_{k-1,i,j}+a_{i,k}+a_{k,j} \right \}ans=i,j,k∈{1..n}min{Tk−1,i,j+ai,k+ak,j}
a i , j a_{i,j}ai,j 表示边 ( i , j ) (i,j)(i,j) 的权值(长度)。
注意,图上必须要有边 ( i , k ) (i,k)(i,k) 和边 ( k , j ) (k,j)(k,j) 才可以。
[code] \color{blue}{\texttt{[code]}}[code]
typedef long long ll;
const ll inf=0x3f3f3f3f3f3f;
ll a[110][110],f[110][110],n,m,ans;
inline void ckmin(ll &a,ll b){
a=min(a,b);//让a取到a,b间较小值
}
int main(){
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
f[i][j]=a[i][j]=inf;
for(int i=1,u,v,w;i<=m;i++){
scanf("%d%d%d",&u,&v,&w);
ckmin(a[u][v],w);ckmin(a[v][u],w);
ckmin(f[u][v],w);ckmin(f[v][u],w);
}
ans=inf;//求最小,初始极大
for(int k=1;k<=n;k++){
for(int i=1;i<k;i++)
for(int j=i+1;j<k;j++)
ckmin(ans,f[i][j]+a[i][k]+a[k][j]);
for(int i=1;i<=n;i++)
if (i!=k&&f[i][k]!=inf)
for(int j=1;j<=n;j++)
if (j!=i&&j!=k&&f[k][j]!=inf)
ckmin(f[i][j],f[i][k]+f[k][j]);
}
if (ans!=inf) printf("%lld",ans);
else printf("No solution.");
return 0;
}
洛谷的P6175就是模板哦。