请点击上面 免费关注本账号!
免费关注本账号!
年度最后一期:美国/欧洲 几何尺寸和公差,苏州站第22期,11.14-15
GD&T系列标准大放送(15本)
GD&T/GPS免费视频课程:ISO辅助框格(四)--组合平面框格(智慧企训学院)
GD&T专题:基准平移和DF--智慧企训学院

准时开课,吴老师授课
在机械工程图中,对于异形曲面,我们只能采用轮廓度(线轮廓度和面轮廓度)进行控制。除了采用常规的轮廓度(即对称轮廓度)控制,还可以采用其他轮廓度,如非对称轮廓度,动态轮廓度,复合轮廓度等等。
今天我们主要聊非对称轮廓度和动态轮廓度。
本期文章我们要讨论的话题有以下几个:
1.ISO/ASME中修饰符号(U圈和UZ)前后的数字表示什么意思?
2. U圈前后的数字可以为负号吗?前后数字的大小有范围要求吗?
3. U圈和动态轮廓度之间是否有关系?
1. 非对称轮廓度
不管是ISO还是ASME,轮廓度默认都是对称分布的。所谓对称分布,指的的是公差带的两个边界相对于理论轮廓是对称分布的(严格意义上讲,不是对称,是两侧的偏置量相同而已),如下图所示:
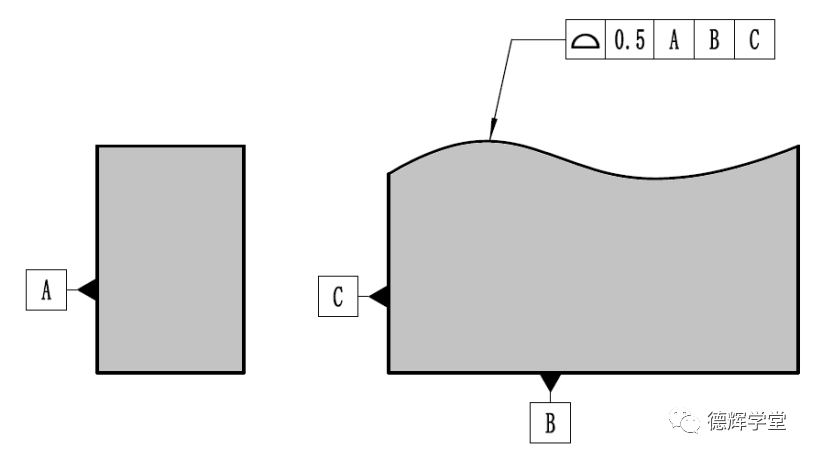
a图纸标注
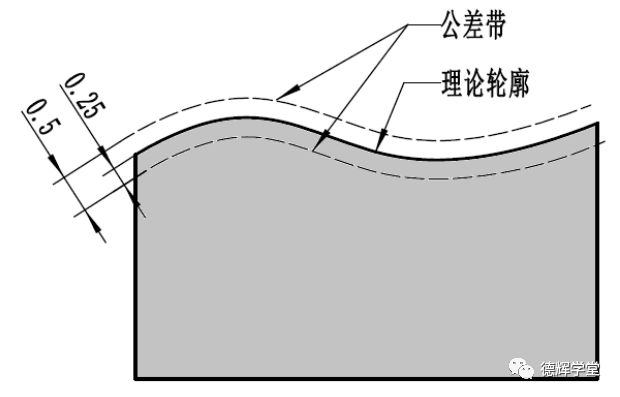
b公差带分布
图1 图纸标注和公差带分布
图1中的宽度为0.5的公差带,是将理论轮廓内外各偏置(Offset)公差带的一半(0.25)形成的,只要被测零件的实际表面能够落在这个宽度为0.5的公差带范围内,该实际被测表面就是合格的。
联想到尺寸要素的尺寸公差,轮廓度其实和下图概念的逻辑是一致的。
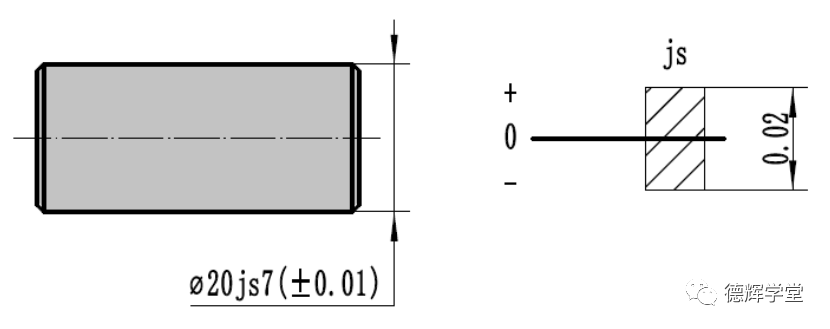
图2 尺寸公差
根据GB/T 1800,图2中Φ20表达的是公称尺寸(即零线),js表达该轴的公差的基本偏差属于对称分布,而7则表示精度等级为IT7,对于公称尺寸为Φ20的尺寸而言,它决定了其公差的大小是0.02(需要查表)。
轮廓度属于几何公差,为什么我们要扯这个尺寸公差呢?因为通过尺寸公差的3大要素(1. 公称尺寸, 2. 基本偏差, 3公差)就可以确定尺寸要素的具体尺寸公差,这个最基本的底层逻辑同样适用于几何公差。
尤其是非对称公差,研究这种最基本的底层逻辑更有意义。
先来看一下非对称轮廓度。
本公众号的第一篇文章就介绍了非对称轮廓度,这里只做简单介绍。先看看美标,见图3:
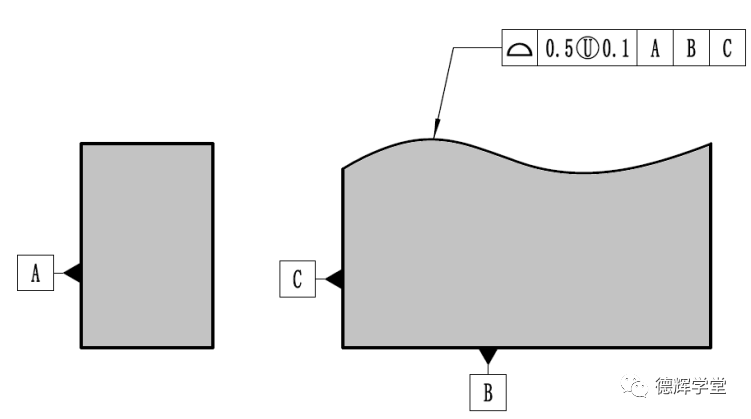
a 图纸标注
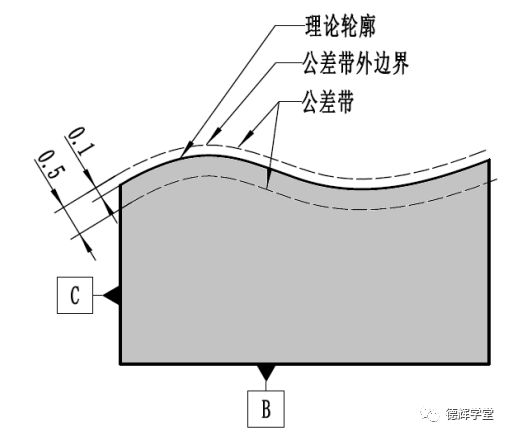
b 公差带分布
图3 非对称轮廓度与公差带
根据图3中的图纸标注,一旦采用U圈(美标),公差带相对于理论轮廓通常就是非对称分布的。那么它是怎么分布的呢?
根据美标Y14.5-2018或者Y14.5-2009中规定,U圈前面的数值表达的是公差值(0.5),U圈后边的数值表达的是公差带外边界相对于理论轮廓在加材料方向的偏置量(0.1),见图3中b图。
需要注意的是,加材料方向,实际上就是理论轮廓的法向(正方向是材料里指向材料外)。
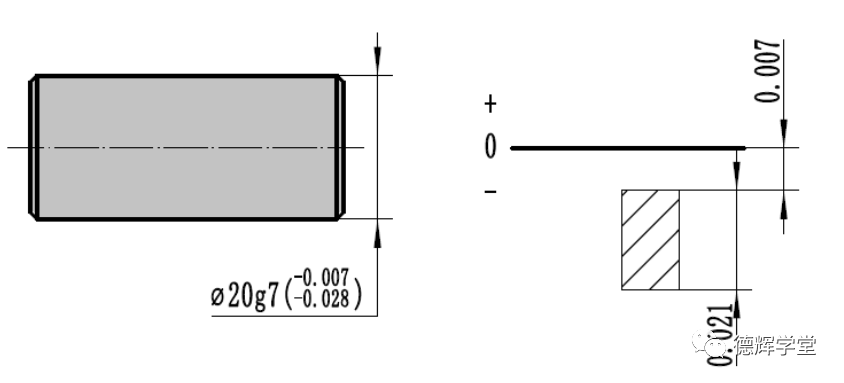
图4 尺寸公差
我们再来扯扯尺寸公差,对比着来认识非对称轮廓度。如果采用公差代号来表达尺寸公差,我们发现除了基本偏差代号为JS和js以外的所有公差都是非对称分布的(建议参考GB/T1800.1或者ISO286-1)。
图4中轴的尺寸公差用公差代号Φ20g7表达,同样,表达尺寸公差的三大要素分别为:
Φ20表达的是公称尺寸,决定了0线的位置
g表达的是基本偏差(孔用大写字母,轴用小写字母),决定了公差相对于0线的偏差为0.007
7决定了公差值的大小为0.021
对比非对称轮廓度公差,同尺寸公差一样,表达它也同样需要三大要素:
理论轮廓(相当于尺寸公差中的公称尺寸Φ20)
偏置量,即U圈后面的数值,表示公差带外边界相对于理论轮廓的偏置量0.1(相当于尺寸公差中的g)
公差带大小,即U圈前面的数值,表示公差带总宽度为0.5(相当于尺寸公差中的7级精度等级)
具体见图5:
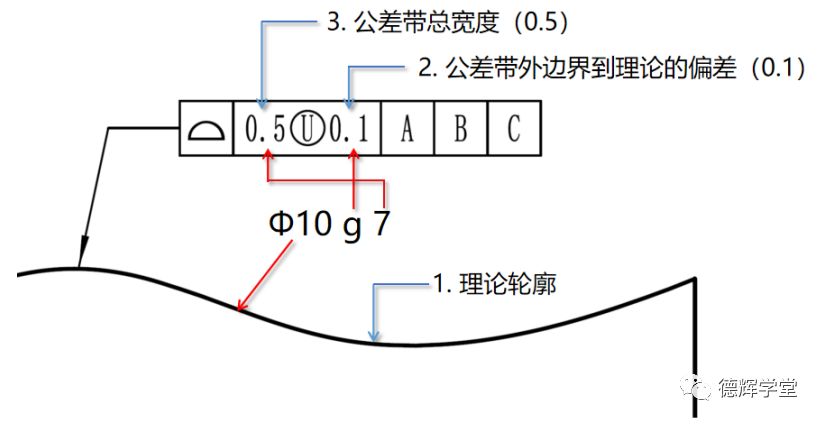
图5 几何公差与尺寸公差的共同逻辑
假如我们用尺寸公差的形式来表达图3中的非对称轮廓度,我们可以说它的要求是+0.1到-0.4(当然,这个仅用于口头交流)。
我们再来看看ISO中的非对称轮廓度是怎么回事。
基于同样的逻辑,认识ISO中的非对称轮廓度就很容易,ISO中非对称公差的修饰符号是UZ(注意,没有圈),见下图:
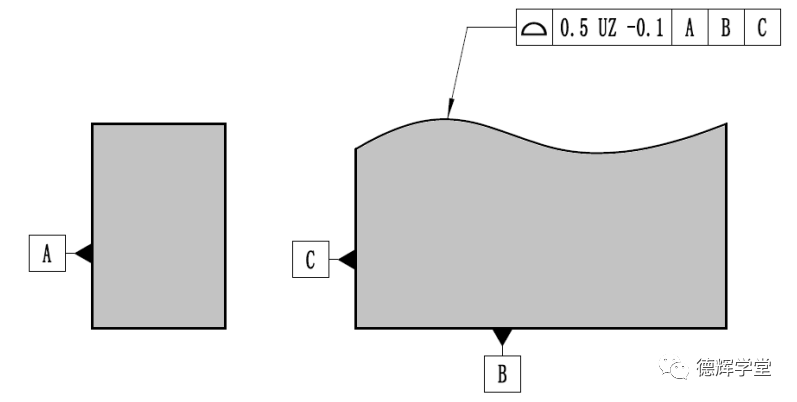
a 图纸标注
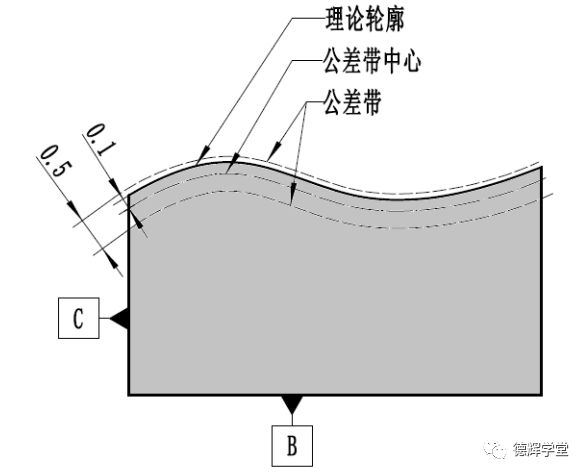
b 公差带分布
图6 ISO图纸标注和公差带分布
根据ISO的概念可知,修饰符号UZ前面的数值表达的是公差带的总宽度0.5,UZ后边的数值表达的是公差带的中心相对于理论轮廓的偏置量0.1(负号表达在公差带中心在材料里边,而正号则表达公差带中心在材料外边)。具体见图6。
我们仔细观察,也会发现ISO也是基于3大要素来表达非对称轮廓度公差的:
理论轮廓。
偏置量,即UZ后边的数值,表示公差带中心相对于理论轮廓的偏置量为0.1,负号表示方向,意思是公差带的中心在材料里边。
公差带大小,即UZ前面的数值,表示公差带总宽度为0.5。
对比ISO和ASME中的非对称轮廓度,UZ和U圈前面的数值都表示公差带的总宽度,这一点两个标准是相同的。唯一差别在于修饰符号U圈和UZ后边的数值,即偏置量的计算方式不一样,起点都是理论轮廓,但终点不一样。
1. ASME表达的是理论轮廓到公差带外边界的偏置量
2. ISO表达的是理论轮廓到公差带中心的偏置量
到这里,我们稍作总结,轮廓度公差的逻辑和尺寸公差的逻辑是一样的,无非就包含3个信息:1. 理论轮廓;2. 偏置量;3. 公差大小。ISO和ASME各自修饰符号(U圈和UZ)前面的数值都表达的是公差带的总宽度,U圈和UZ后边都表达的是偏置量,只是U圈的偏置量是从公差带外边界开始算,UZ的偏置量是从公差带中心开始算。
设计工程师为什么要采用非对称轮廓度呢?
如同尺寸公差要采用非对称公差一样,常见的应用工况之一就是为了“配合”。比如下图所示:
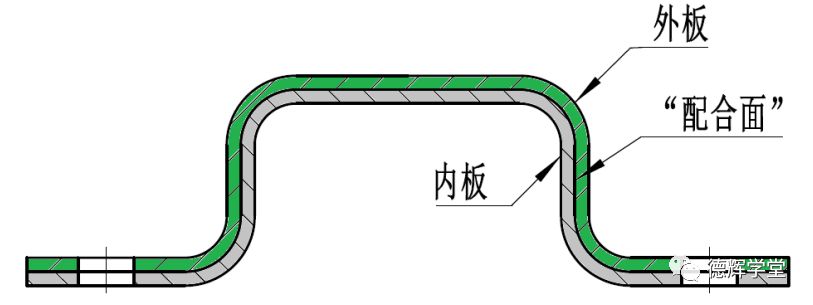
图7 内外板
图7中的外板和内板会焊接在一起,内板主要起到加强作用。内外板的“配合面”在数模上是零贴的,在焊接之前,我们希望外板的内槽大一些,内板则小一些。也就是说我能希望外板和内板之间的配合属于间隙配合。
这时,我们就可以采用非对称轮廓度控制,见图8和图9。
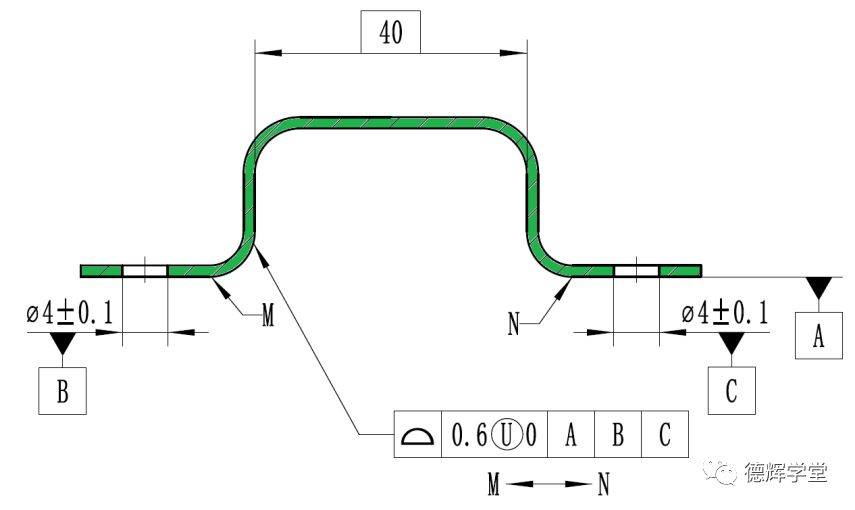
图8 外板图纸
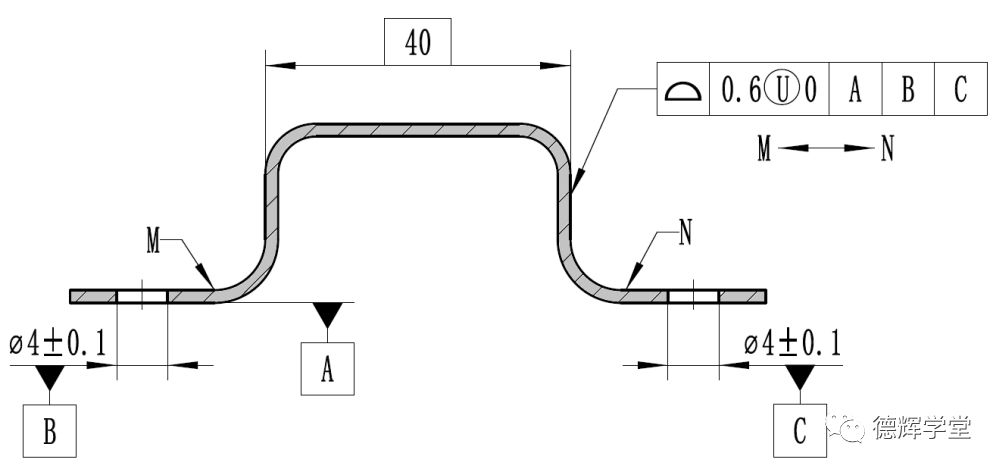
图9 内板图纸
图8中外板的配合面(内槽)采用非对称轮廓度控制,公差带相当于0到-0.6,这样会导致图8中内槽宽40的实际尺寸只会偏大,不会偏小。而图9中正好相反,它的公差带也是0到-0.6,会导致(外凸)宽度40的实际尺寸只会偏小,不会偏大。能够实现“间隙配合”。
具体偏大多少,偏小多少,我们把它设置成一道练习题,放在文章最后,供大家练习用。
2. U圈和UZ前后数值的范围
接下来,进入在业界经常争论的一个话题,U圈前边和后边的数值是否都可以为负?U圈后边数值大小是否一定要比U圈前边的数值小?
这个话题之所以会成为业界争论的一个话题,那是因为根据最权威的依据-ASME Y14.5-2018, 对该话题它没有给出明确的说法,所以行业内不同的老师可能有不同的看法。
但是,标准没有明确说明,并不代表我们的观点可以没有依据,我们仍可以根据标准更深层次的逻辑和思路来讨论上述话题。
我先说明我个人的观点:
U圈前面的数值只能为正值,不能为负值,更不能为0。理由:因为U圈前边的数值表达的是公差值的大小,即公差带的宽度。公差带的宽度不能为负值和0。
U圈后边的数值,可以为正值,也可以为负值,也可以为0。理由:U圈后边的数值表达的是偏置量,偏置量可正可负,正负号表示方向,取决于公差带的外边界相对于理论轮廓的位置,如果公差带外边界是在法向正方向处(材料以外),为正,在法向负方向处(材料里边)则为负,如果刚好在理论轮廓上,则为0。
U圈后边的数值和U圈前面的数值没有任何关系,可以比前边的数值大,也可以比前面的数值小。理由:U圈前面表示公差,U圈后边表示偏差,偏差和公差没有直接关系,所以U圈后边的数值比U圈前面的数值可以大,也可以小。
我们姑且把上面的结论称为“3大结论”。
那么ISO中的UZ呢?UZ在ISO标准(可参考ISO1101:2017)中的规范相应明确,上面3条也完全成立!具体见图10
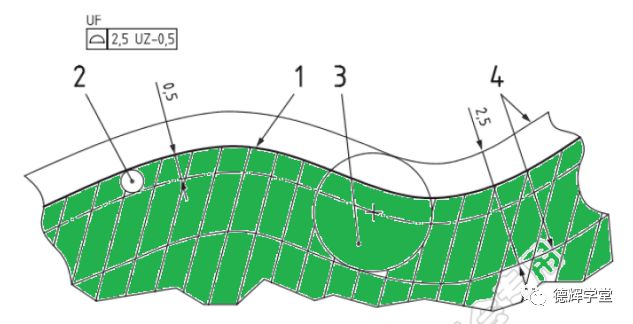
图10 ISO中的非对称轮廓度
图10是ISO标准对非对称轮廓度的解释,1表示理论轮廓,2号球球的直径是0.5,表达公差带中心相对理论轮廓的偏置量是0.5,因为在材料内部,所以要加负号,3号球球的直径是2.5,表达公差带的总宽度,4表示公差带的两个边界。
所以ISO这个UZ修饰符号前后数值的游戏规则,完全符合上面提到的3大结论。
讲到这里,可能有很多小伙伴表示不服气。你从头到尾都在拿非对称轮廓度和尺寸公差做对比,所以你认为他们逻辑或者思路就应该一样,是不是有点牵强?
确实有点牵强,接下来,我们死磕标准。
像基督徒一样证明针尖上究竟能站几个天使,要死磕圣经。
美标里,U圈前面的数值为什么不能为负?要回答该问题,我们首先应该回答下面这个问题,U圈前面的数值究竟表达什么含义?标准里也说得很清楚,具体见Y14.5-2018,P241:

图11 美标中的定义
图11中红线部分,可以翻译成“在公差控制框格里,将非对称符号(U圈)放在公差值后边。”这句话就意味着,U圈前面的数值表达的是公差值!公差值是公差带的宽度或者直径,数值当然不能为负(几何公差中,你找个负的公差值出来给我看看?)。
所以上面3大结论中第一条成立的。
有小伙伴又会问,你凭什么胡咧咧三大结论中的第2条和第3条成立呢?
确实,在标准中我找不出直接的证据。
但是,如果我把3大结论中的第2条和第3条换个角度来问:
U圈后边的数值,为什么不可以为负?
U圈后边的数值为什么不能比U圈前面的数值大?
你能理直气壮的说出理由吗,举个例子也行啊?
我们会发现,我们其实找不到个硬核的理由来反驳三大结论中的第2条和第3条。相反,我倒能找到支持3大结论中的第2条和第3条的案例。比如说动态轮廓度。
接下来,我们就讨论讨论最新标准出现的动态轮廓度(Dynamic Profile )
3. 动态轮廓度和非对称轮廓度
动态轮廓度(Dynamic Profile)是最新的美标(Y14.5-2018)推出的一个概念,它的修饰符号是一个朝上的等腰三角形。这个符号我个人的感觉是抄袭(说参考,或者对应也行)ISO中的修饰符号OZ。
不管怎样,这个符号是一个非常重要的发明,在控制“相似度”上更加实用。关于它的用处,我们下一篇文章讨论。我们先讨论它的基本概念。具体见下图:
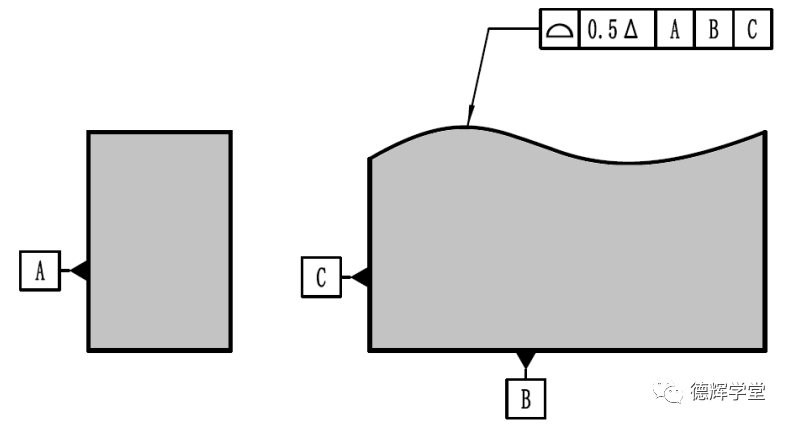
a 动态轮廓度图纸标注
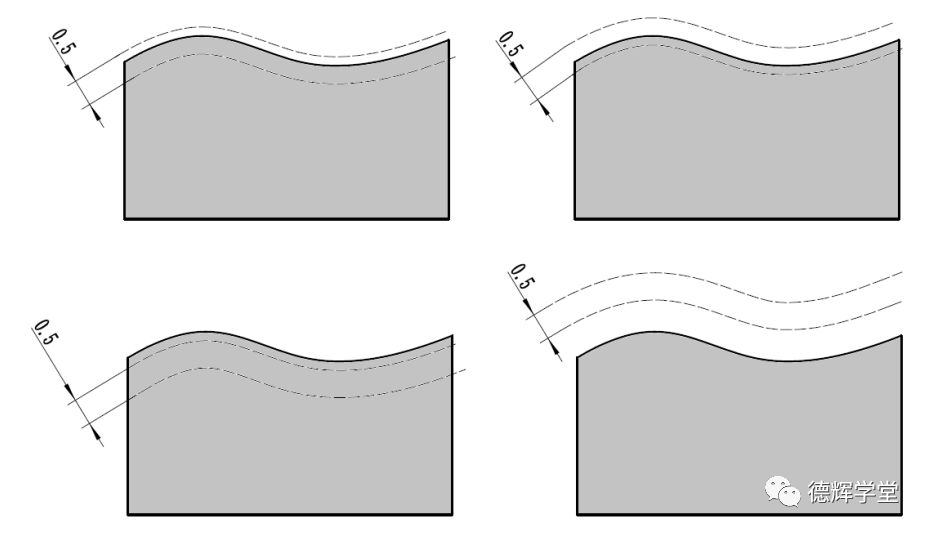
b 动态轮廓度的公差带分布
图12 动态轮廓度与公差带分布
图12中表达的是动态轮廓度和公差带分布,注意观察b图中公差带的特点,公差带的边界是由理论轮廓偏置而来,偏置量为任意值,注意,是任意值,即偏置量为任意常数。但是公差带的总宽度为0.5,这个固定不变。
也就是说,公差带可以相对理论轮廓无限往材料外“扩张”,也可以无限往材料内“收缩”。只要实际轮廓能够落在0.5的公差带范围内就合格。
还不太明白?我们换个方式来表示动态轮廓度,我们用非对称轮廓度来表达动态轮廓度:

图13 ASME中非对称轮廓度和动态轮廓度
图13用非对称轮廓来表达动态轮廓度,需要注意的是,非对称轮廓度U圈后边的字母d(偏置量)可以为任意值。见下图:
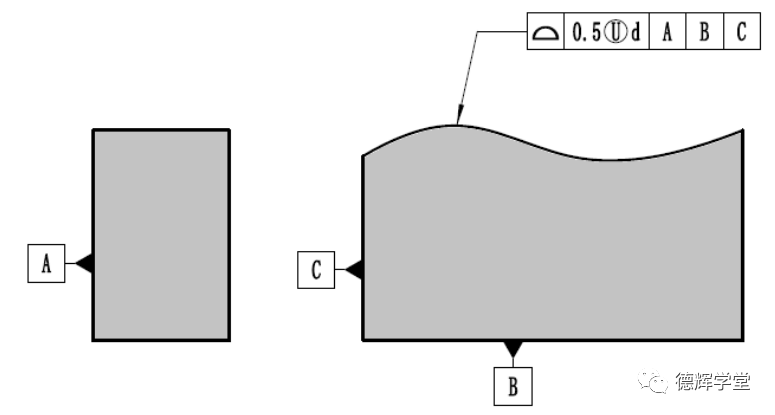
a 图纸标注
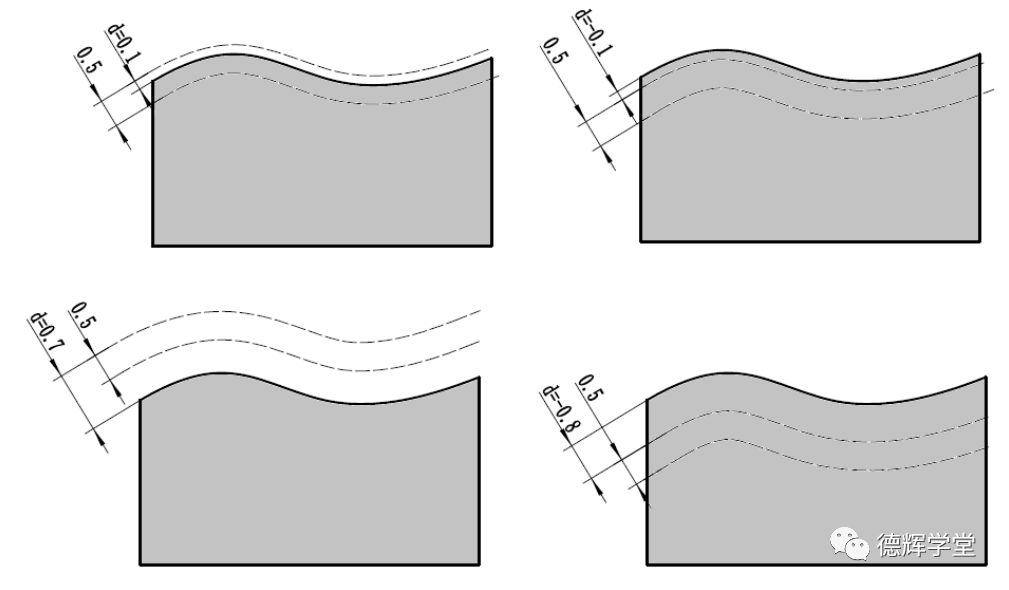
b 公差带分布
图14 d为任意值的非对称轮廓度
图14用的是偏置量d为任意值的非对称轮廓度,它其实就是动态轮廓度的另外一种表达。通过对动态轮廓公差带的观察,我们不难发现,作为轮廓度公差的一种,它的公差带可以完全超出理论轮廓,也可以完全在理论轮廓以内。
也就是说,不管你愿不愿意,对动态轮廓度来说,图14中的d值,可以为负值,可以为正值,还可以大于U圈前面的数值。
既然公差带允许如此偏置,非对称轮廓度为什么不可以?非对称轮廓度的公差带完全脱离理论轮廓难道会死人?
我们回头仔细一想,会发现,非对称轮廓度和动态轮廓度之间的关系如下:
动态轮廓度就是偏置量为任意值的非对称轮廓度。而非对称轮廓度则是公差带处于特定位置的动态轮廓度。(这个特定位置可以完全处于材料里边即理论轮廓以内,或者完全在材料外边,即理论轮廓以外)
所以,通过对动态轮廓度的深度认识,就逻辑来说,我们会发现,3大结论中的第2条,第3条结论没有理由不能成立。
通过对ASME的非对称轮廓度和动态轮廓度的分析,我们再对ISO的分析就相对容易的多。ISO中用OZ来表达美标“动态轮廓度”的概念,中文叫“未定义偏置量的轮廓度”,它和ISO中的非对称轮廓度也满足以下关系:

图15 ISO中非对称轮廓度和未定义偏置量轮廓度
图15中, 带OZ修饰符号的未定义偏置量轮廓度,相当于偏置量d为任意值的非对称轮廓度。
显然,对于ASME中的动态轮廓度和ISO中的未定义偏置量的轮廓度是同一个概念,因为是偏置量为任意值,那么偏置量的终点从公差带哪里开始计算也就不重要了。所以有以下等式成立:

图16 两个标准中偏置量为任意值的轮廓度
好了,篇幅太长了,本期的文章先到这里。
相信你还有问题,比如动态轮廓度应用在哪些方面?动态轮廓度可以单独使用吗?动态轮廓度如何检测?动态轮廓度和复合轮廓度有区别吗?欢迎您继续关注本公众号,我们下期将深入讨论动态轮廓度。
在小结之前,我们先做一个小调查,看了本期的文章后,对于U圈前后边的数值,你的观点是什么呢?
你有更多的话不吐不快?对作者的胡说八道恨之入骨?欢迎给我们留言!
本文小结
本期文章探讨了ISO和ASME中的非对称轮廓度,比较了两者的异同。同时将非对称轮廓度和动态轮廓度进行对比,得出了三大结论,并利用动态轮廓度的思路证明了3大结论成立。
课后练习:
已知零件图纸如下图所示,基于对非对称轮廓度的认识,请问EF面之间的距离的变化范围是多少?
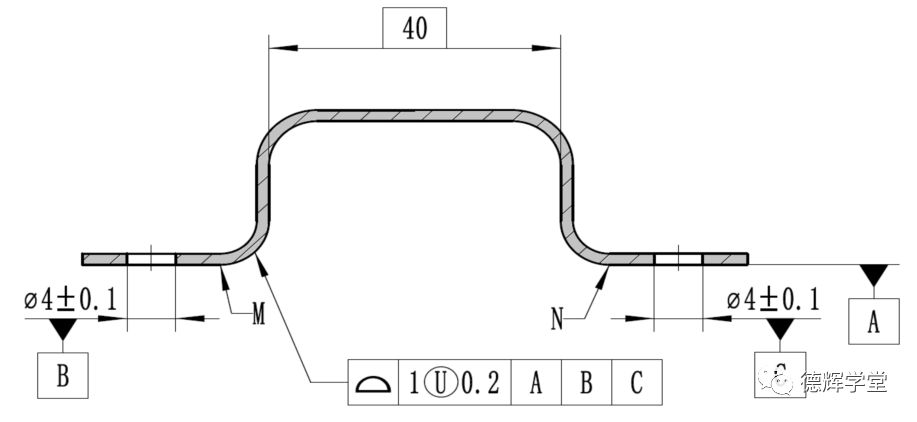
图18 图纸标注
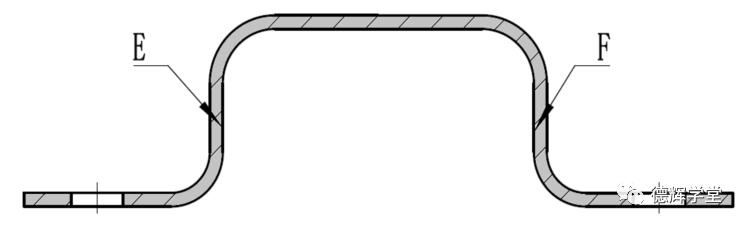
图19 EF面之间的距离变化范围
答案: 已知零件图纸如下图所示,基于对非对称轮廓度的认识,请问EF面之间的距离的变化范围是多少?
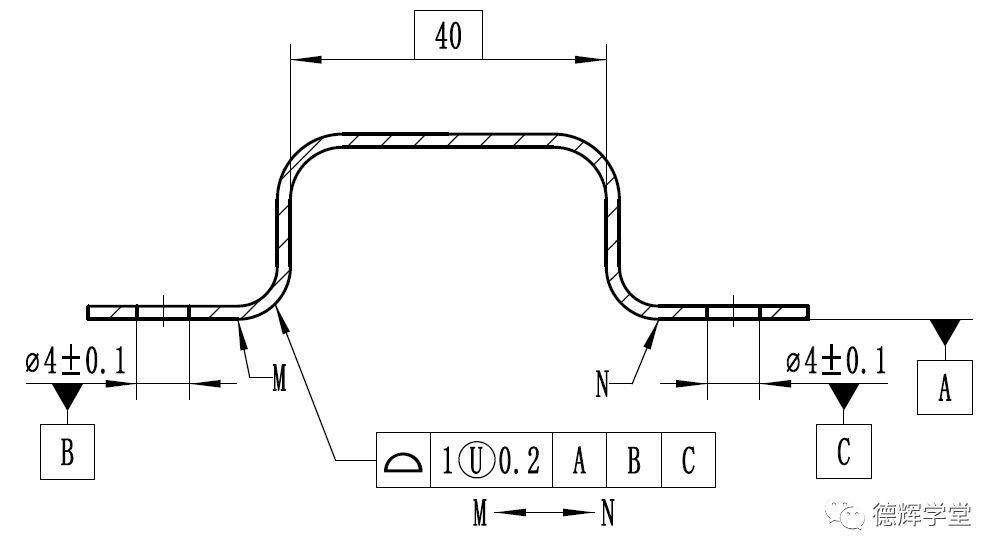
图1图纸标注a
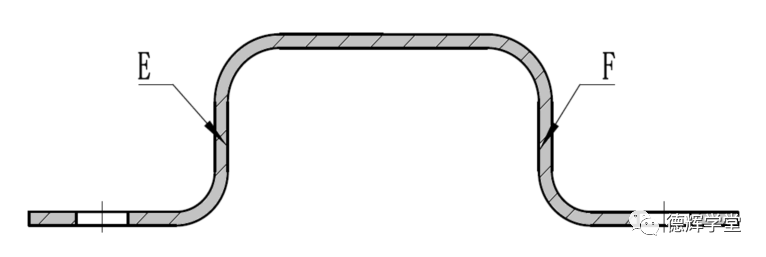
图2 EF面之间的距离变化范围
要解释这个问题,首先要画出公差带,公差带如下图所示:
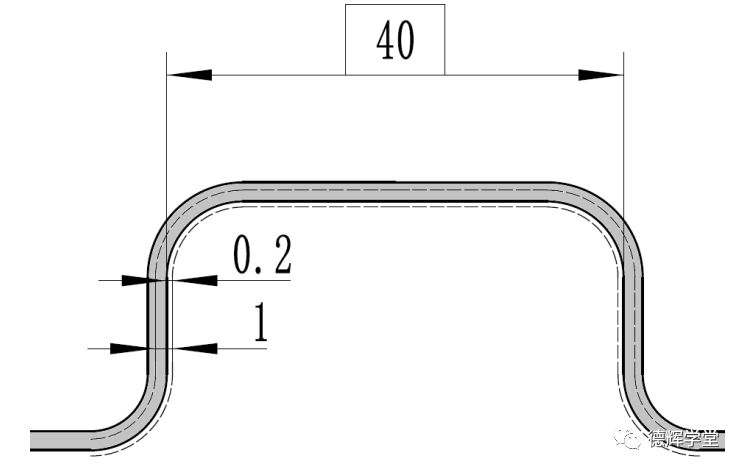
图3 公差带分布
基于图3的公差带分布,我们不难求出EF之间的最大值和最小值,见图4.
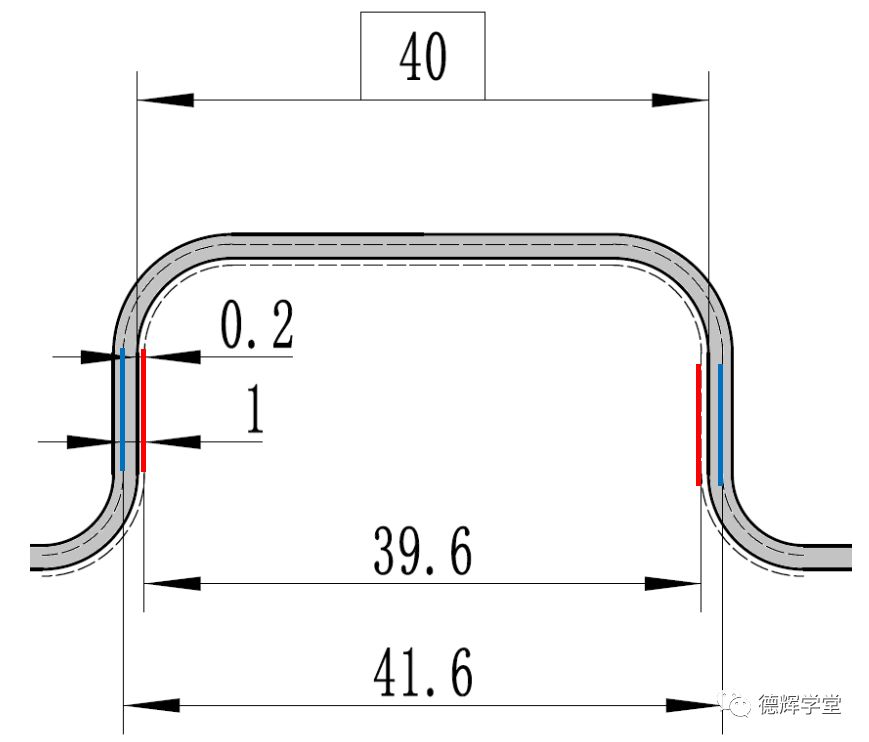
图4 EF距离的最大值和最小值
根据图4可以看出,显然,当实际的被测面处于公差带的外边界时(如两红线位置),EF距离最小,最小值为40-0.2-0.2=39.6。
当实际的被测面处于公差带的内边界时(如蓝线位置),EF距离最大,最大值为 40+0.8+0.8=41.6。
您做对了吗?

免责声明:本文来自网络,版权归原作者所有,本文内容为原作者观点,并不代表本公众号赞同其观点和对其真实性负责。
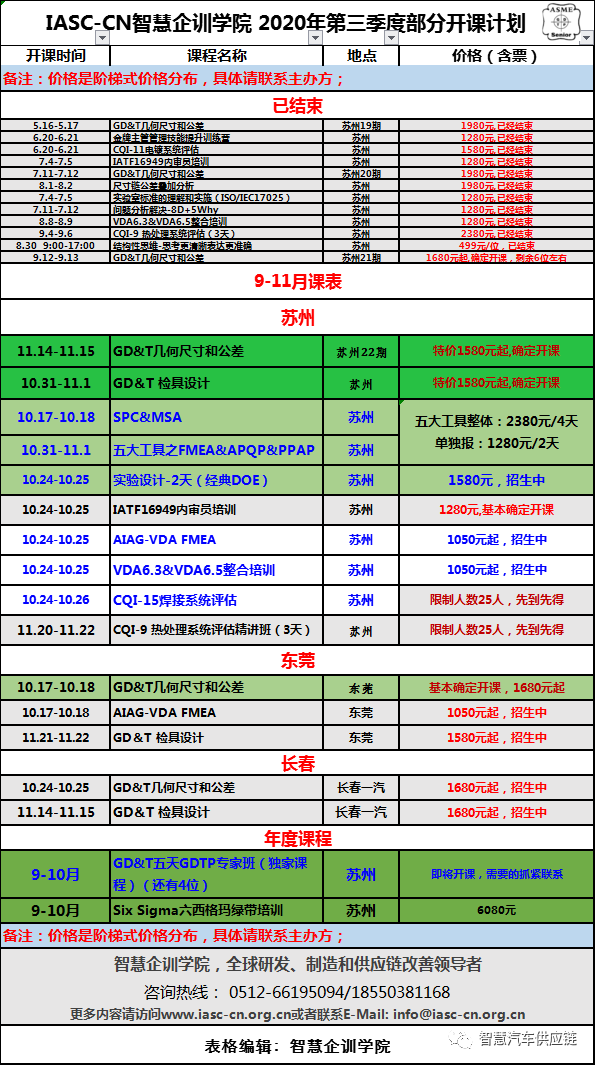
必读 → 收藏!2020年智慧汽车供应链俱乐部&智慧企培学院 课程计划
邀请您免费听DFMEA网课
近期公益课程
工厂产品和过程管控
加入中国智慧汽车供应链俱乐部大群,跟同行一起交流经验,学习更多

更多问题,请添加小编微信,添加时请备注好:公司+职位+姓名
智慧汽车供应链五群 941135777 GD&T专业群:232776212

还请点个赞,点个在看哦,感谢