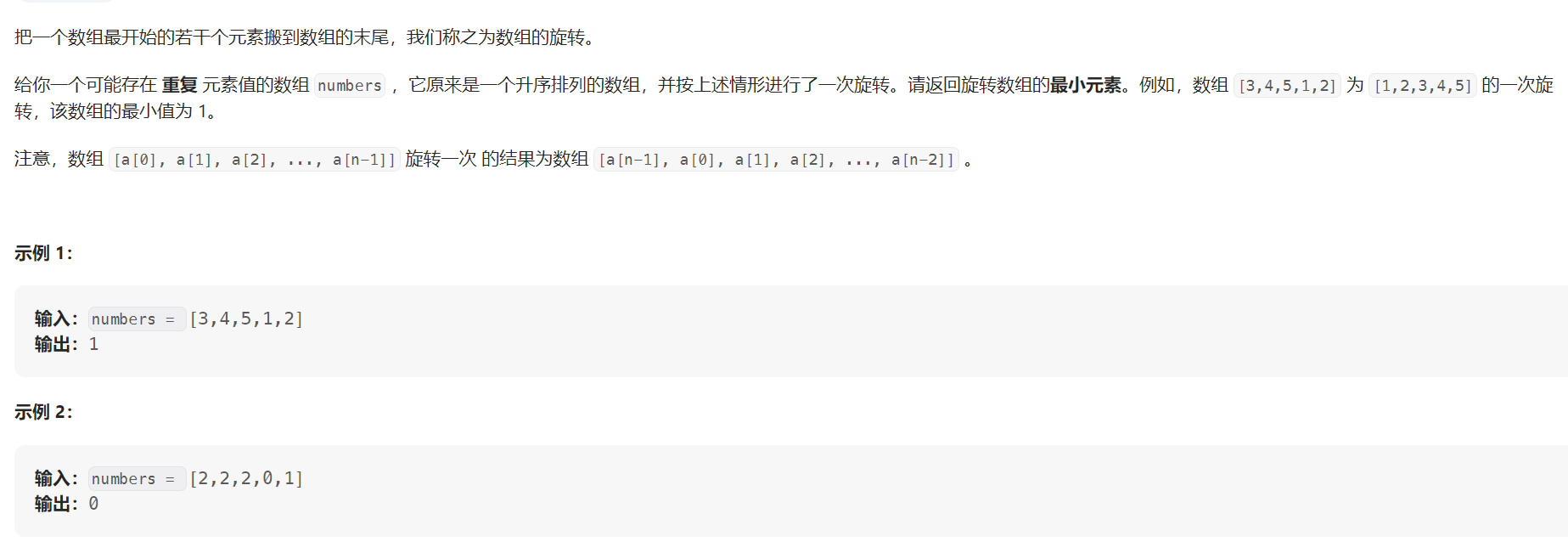
1.旋转数组的最小数字

添加链接描述

• 每次递归将中间值和右侧值相比，划分为三种情况
• 保证最小值在每次指定的搜索区间内

class Solution {
    public int minArray(int[] numbers) {
        return binarySearch(numbers, 0, numbers.length - 1);
    }

    private int binarySearch(int[] numbers, int start, int end) {
        // 递归出口
        if (start >= end) {
            return numbers[start];
        }
        // 中间值和右侧值相比，分为三种情况
        int mid = (start + end) / 2;
        if (numbers[mid] > numbers[end]) {
            start = mid + 1;
        } else if (numbers[mid] < numbers[end]) {
            end = mid;
        } else {
            end--;
        }
        return binarySearch(numbers, start, end);
    }
}

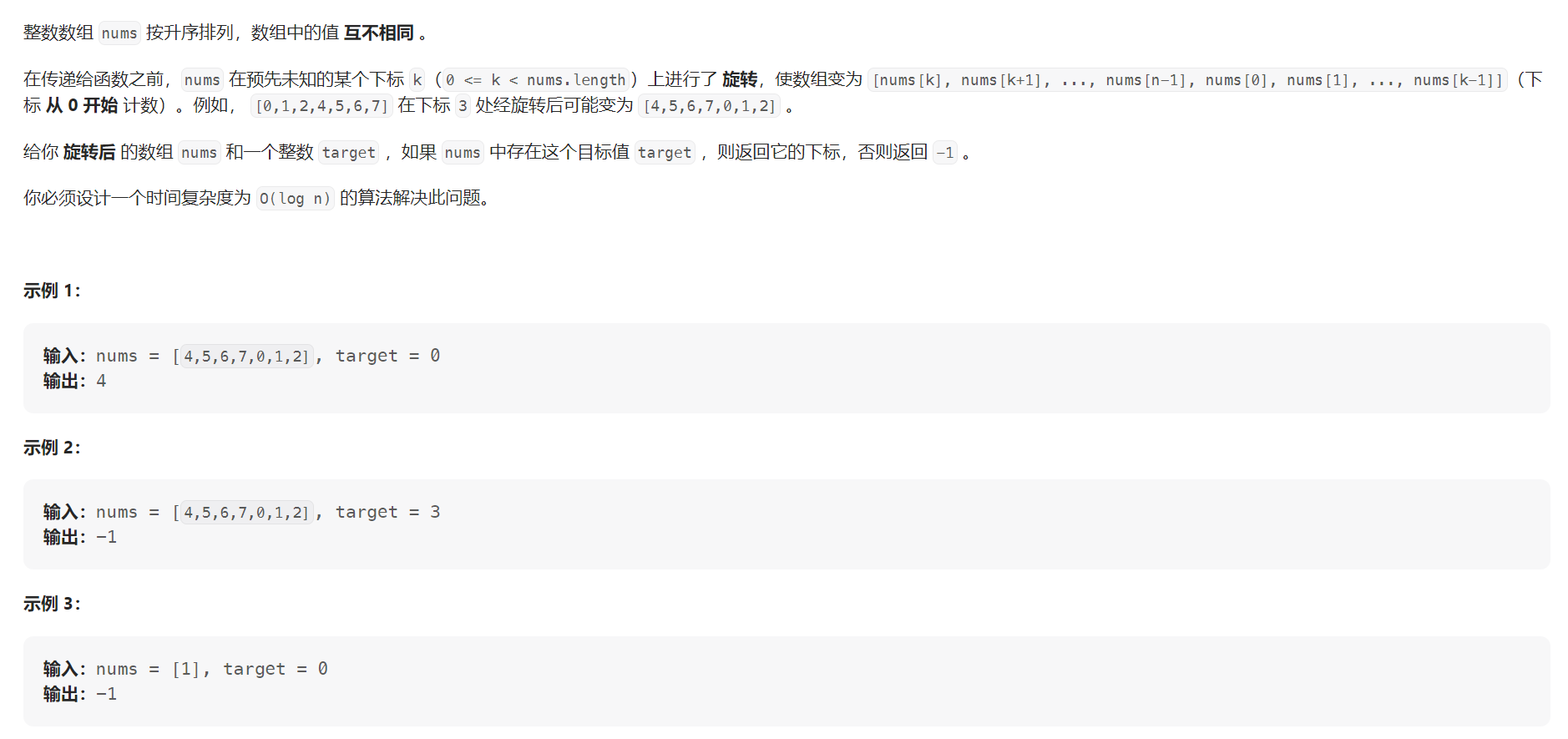
2.旋转数组的目标值下标

添加链接描述

• 先找到旋转数组的最小值下标，然后在两个有序数组中二分查找目标值

class Solution {
    public int search(int[] nums, int target) {
        int minIdx = findMinIdx(nums, 0, nums.length - 1);
        return Math.max(binarySearch(nums, target, 0, minIdx - 1), binarySearch(nums, target, minIdx, nums.length - 1));
    }

    /**
    寻找最小值下标
     */
    private int findMinIdx(int[] nums, int start, int end) {
        if (start > end) {
            return -1;
        } else if (start == end) {
            return start;
        }
        int mid = (start + end) / 2;
        if (nums[mid] < nums[end]) {
            return findMinIdx(nums, start, mid);
        } else {
            return findMinIdx(nums, mid + 1, end);
        }
    }

    /**
    在有序数组中，二分法查找目标值下标
     */
    private int binarySearch(int[] nums, int target, int start, int end) {
        // 递归出口
        if (start > end) {
            return -1;
        }
        int mid = (start + end) / 2;
        if (nums[mid] == target) {
            return mid;
        } else if (nums[mid] > target) {
            return binarySearch(nums, target, start, mid - 1);
        } else {
            return binarySearch(nums, target, mid + 1, end);
        }
    }
}

3.0~n-1缺失的数字

添加链接描述

class Solution {
    public int missingNumber(int[] nums) {
        // 特判：少了第一个数字
        if (nums[0] == 1) {
            return 0;
        }
        // 特判：少了最后一个数字
        if (nums[nums.length - 1] == nums.length - 1) {
            return nums.length;
        }
        return binarySearch(nums, 0, nums.length - 1);
    }

    private int binarySearch(int[] nums, int start, int end) {
        // 递归出口
        if (start >= end) {
            return start;
        }
        int mid = (start + end) / 2;
        if (nums[mid] > mid) {
            if (nums[mid - 1] == mid - 1) {
                return mid;
            } else {
                end = mid - 1;
            }
        } else {
            start = mid + 1;
        }
        return binarySearch(nums, start, end);
    }
}

4.寻找峰值

添加链接描述

• 上坡一定有坡顶，因为超出数组范围就是负无穷，所以每次选择更高的方向递归

class Solution {
    public int findPeakElement(int[] nums) {
        if (nums.length == 1) {
            return 0;
        }
        return binarySearch(nums, 0, nums.length - 1);
    }

    private int binarySearch(int[] nums, int l, int r) {
        if (l > r) {
            return -1;
        }
        int mid = (l + r) / 2;
        // 当前位置是峰值
        if ((mid > 0 && mid < nums.length - 1 && nums[mid - 1] < nums[mid] && nums[mid + 1] < nums[mid]) || (mid == 0 && nums[0] > nums[1]) || (mid == nums.length - 1 && nums[nums.length - 1] > nums[nums.length - 2])) {
            return mid;
        }
        // 当前位置不是峰值：【上坡一定有坡顶，因为超出数组范围就是负无穷】
        if (mid >= 1 && nums[mid - 1] > nums[mid]) {  
            return binarySearch(nums, l, mid - 1);
        } else {
            return binarySearch(nums, mid + 1, r);
        }
    }
}

5.在排序数组中寻找目标值的开始和结束位置

添加链接描述

• 方法1：二分法找到目标值，并向左右扩展

class Solution {

    public int[] searchRange(int[] nums, int target) {
        // 二分法查找，然后左右扩展
        int idx = binarySearch(nums, target, 0, nums.length - 1);
        if (idx == -1) {
            return new int[]{-1, -1};
        }
        int l = idx;
        int r = idx;
        while (l >= 0 && nums[l] == target) {
            l--;
        }
        while (r < nums.length && nums[r] == target) {
            r++;
        }
        return new int[]{l + 1, r - 1};
    }

    private int binarySearch(int[] nums, int target, int start, int end) {
        if (start > end) {
            return -1;
        }
        int mid = (start + end) / 2;
        if (nums[mid] == target) {
            return mid;
        } else if (nums[mid] < target) {
            return binarySearch(nums, target, mid + 1, end);
        } else {
            return binarySearch(nums, target, start, mid - 1);
        }
    }
}

• 方法2：两次二分法

class Solution {
    public int[] searchRange(int[] nums, int target) {
        return new int[]{binarySearch(nums, target, 0, nums.length - 1, true), binarySearch(nums, target, 0, nums.length - 1, false)};
    }

    private int binarySearch(int[] nums, int target, int start, int end, boolean findLeftIndex) {
        // 递归出口
        if (start > end) {
            return -1;
        }
        if (start == end) {
            return (nums[start] == target) ? start : -1;
        }
        int mid = (start + end) / 2;
        if (nums[mid] == target) {
            // 找到左边界
            if (findLeftIndex && ((mid > 0 && nums[mid - 1] != target) || mid == 0)) {
                return mid;
            } else if (findLeftIndex) {
                return binarySearch(nums, target, start, mid - 1, findLeftIndex);
            }
            // 找到右边界
            if (!findLeftIndex && ((mid < nums.length - 1 && nums[mid + 1] != target) || mid == nums.length - 1)) {
                return mid;
            } else {
                return binarySearch(nums, target, mid + 1, end, findLeftIndex);
            }
        } else if (nums[mid] < target) {
            return binarySearch(nums, target, mid + 1, end, findLeftIndex);
        } else {
            return binarySearch(nums, target, start, mid - 1, findLeftIndex);
        }
    }
}