点击蓝字
关注我们
TSP
问题
PART 01
问题提出
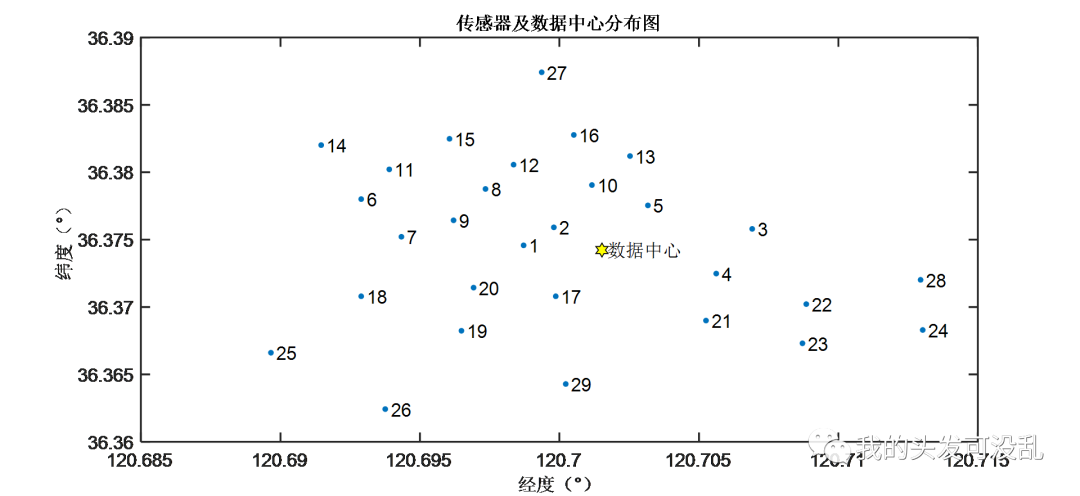
图1|坐标分布图
数据中心为某辆充电小车的出发点,坐标1~坐标29为29个充电点,充电小车需从数据中心出发并且依次经过29个充电点,最后回到数据中心。为使路线总路径最短,需确定充电小车每一步该怎么走,这就是典型的TSP问题。
模型建立

TSP求解算法对比
蚁群算法求解TSP问题

求解结果
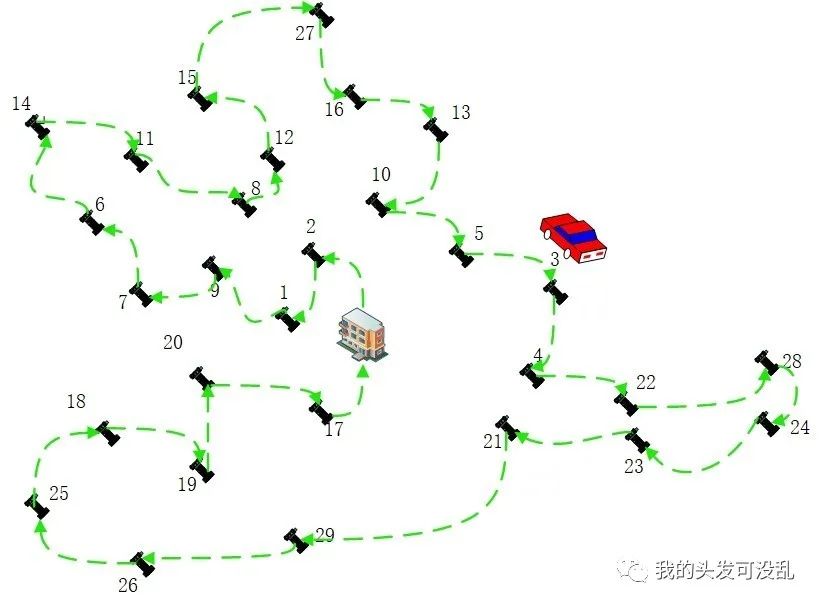
图2|移动小车充电路线图
MTSP
问题
PART 02
问题提出
当数据中心含有4辆小车时,4辆小车需要合作完成充电任务,即每辆小车负责一部分充电点的充电,并且使总路程最短,该问题为典型的多旅行社问题,即MTSP问题。
模型建立

遗传求解MTSP问题

求解结果
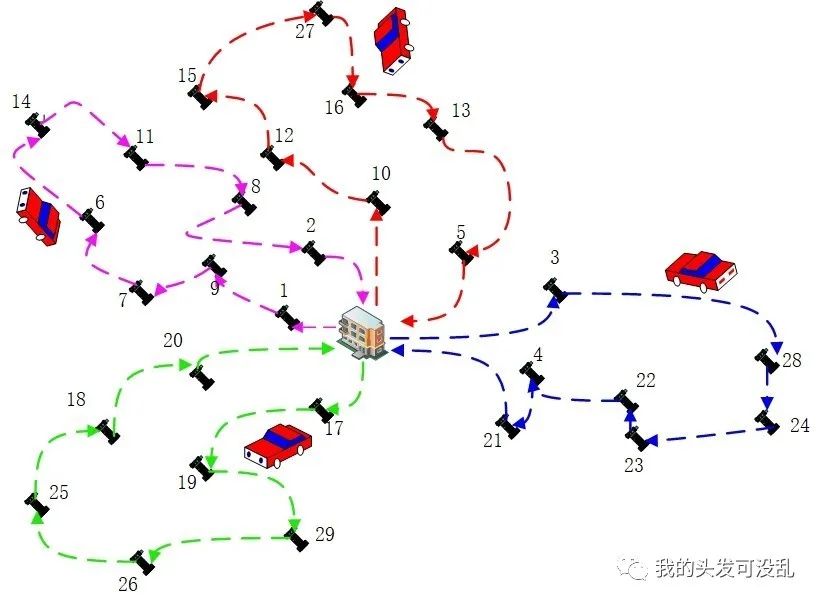
图3|多移动小车充电路线图
MATLAB源代码
蚁群算法求解TSP问题
clc;clf;clear;data1 = xlsread('附件1.xlsx');x = data1(:,1);y = data1(:,2);X = data1(:,1:2);[N,n]=size(X); % N =测试样本数;n =测试样本的属性数;K = 4; % K = 组数; R = 100; % R = 蚂蚁数; t_max = 1000; % t_max =最大迭代次数; % 初始化c = 10^-2;tau = ones(N,K) * c; %信息素矩阵,初始值为0.01的N*K矩阵(样本数*聚类数)q = 0.9; % 阈值qrho = 0.1; % 蒸发率best_solution_function_value = inf; % 最佳路径度量值(初值为无穷大,该值越小聚类效果越好)tict = 1; % while ((t<=t_max)) %达到最大迭代次数而终止% while ((best_solution_function_value>=19727)) %达到一定的聚类效果而终止while ((best_solution_function_value>=19727)) %路径标识字符:标识每只蚂蚁的路径 solution_string = zeros(R,N+1); for i = 1 : R %以信息素为依据确定蚂蚁的路径 r = rand(1,N); %随机产生值为0-1随机数的1*51的数组 for g = 1 : N if r(g) < q %如果r(g)小于阈值 tau_max = max(tau(g,:)); Cluster_number = find(tau(g,:)==tau_max); %聚类标识数,选择信息素最多的路径 solution_string(i,g) = Cluster_number(1); %确定第i只蚂蚁对第g个样本的路径标识 else %如果r(g)大于阈值,求出各路径信息素占在总信息素的比例,按概率选择路径 sum_p = sum(tau(g,:)); p = tau(g,:) / sum_p; for u = 2 : K p(u) = p(u) + p(u-1); end rr = rand; for s = 1 : K if (rr <= p(s)) Cluster_number = s; solution_string(i,g) = Cluster_number; break; end end end end % 计算聚类中心 weight = zeros(N,K); for h = 1:N %给路径做计算标识 Cluster_index = solution_string(i,h); %类的索引编号 weight(h,Cluster_index) = 1; %对样本选择的类在weight数组的相应位置标1 end cluster_center = zeros(K,n); %聚类中心(聚类数K个中心) for j = 1:K for v = 1:n sum_wx = sum(weight(:,j).*X(:,v)); %各类样本各属性值之和 sum_w = sum(weight(:,j)); %各类样本个数 if sum_w==0 %该类样本数为0,则该类的聚类中心为0 cluster_center(j,v) =0 continue; else %该类样本数不为0,则聚类中心的值取样本属性值的平均值 cluster_center(j,v) = sum_wx/sum_w; end end end % 计算各样本点各属性到其对应的聚类中心的均方差之和,该值存入solution_string的最后一位 F = 0; for j= 1:K for ii = 1:N Temp=0; if solution_string(i,ii)==j; for v = 1:n Temp = ((abs(X(ii,v)-cluster_center(j,v))).^2)+Temp; end Temp = sqrt(Temp); end F = (Temp)+F; end end solution_string(i,end) = F; end %根据F值,把solution_string矩阵升序排序 [fitness_ascend,solution_index] = sort(solution_string(:,end),1); solution_ascend = [solution_string(solution_index,1:end-1) fitness_ascend]; for k=1:R if solution_ascend(k,end)<=best_solution_function_value best_solution = solution_ascend(k,:); end k = k+1; end % 用最好的L条路径更新信息数矩阵 tau_F = 0; L=2; for j = 1:L tau_F = tau_F + solution_ascend(j,end); end for i = 1 : N tau(i,best_solution(1,i)) = (1 - rho) * tau(i,best_solution(1,i)) + 1/ tau_F; %1/tau_F和rho/tau_F效果都很好 end t=t+1 best_solution_function_value = solution_ascend(1,end) endtime=toc;clct timecluster_centerbest_solution = solution_ascend(1,1:end-1);IDY=ctranspose(best_solution)best_solution_function_value = solution_ascend(1,end)%分类结果显示%plot3(cluster_center(:,1),cluster_center(:,2),cluster_center(:,3),'o');grid;boxplot(cluster_center(:,1),cluster_center(:,2),'o');grid;boxtitle('蚁群聚类结果(R=100,t=10000)')xlabel('X')ylabel('Y')zlabel('Z')YY=[1 2 3 4];index1 = find(YY(1) == best_solution)index2 = find(YY(2) == best_solution)index3 = find(YY(3) == best_solution)index4 = find(YY(4) == best_solution)line(X(index1,1),X(index1,2),'linestyle','none','marker','*','color','g');line(X(index2,1),X(index2,2),'linestyle','none','marker','*','color','r');line(X(index3,1),X(index3,2),'linestyle','none','marker','+','color','b');line(X(index4,1),X(index4,2),'linestyle','none','marker','s','color','b');rotate3d%代码参考:CSDN
遗传算法求解MTSP问题
function varargout = mtspf_ga(xy,dmat,salesmen,min_tour,pop_size,num_iter,show_prog,show_res)nargs = 8;for k = nargin:nargs-1 switch k case 0 xy = 10*rand(40,2); case 1 N = size(xy,1); a = meshgrid(1:N); dmat = reshape(sqrt(sum((xy(a,:)-xy(a',:)).^2,2)),N,N); case 2 salesmen = 5; case 3 min_tour = 2; case 4 pop_size = 80; case 5 num_iter = 5e3; case 6 show_prog = 1; case 7 show_res = 1; otherwise endend% Verify Inputs[N,dims] = size(xy);[nr,nc] = size(dmat);if N ~= nr || N ~= nc error('Invalid XY or DMAT inputs!')endn = N - 1; % Separate Start/End City% Sanity Checkssalesmen = max(1,min(n,round(real(salesmen(1)))));min_tour = max(1,min(floor(n/salesmen),round(real(min_tour(1)))));pop_size = max(8,8*ceil(pop_size(1)/8));num_iter = max(1,round(real(num_iter(1))));show_prog = logical(show_prog(1));show_res = logical(show_res(1));% Initializations for Route Break Point Selectionnum_brks = salesmen-1;dof = n - min_tour*salesmen; % degrees of freedomaddto = ones(1,dof+1);for k = 2:num_brks addto = cumsum(addto);endcum_prob = cumsum(addto)/sum(addto);% Initialize the Populationspop_rte = zeros(pop_size,n); % population of routespop_brk = zeros(pop_size,num_brks); % population of breaksfor k = 1:pop_size pop_rte(k,:) = randperm(n)+1; pop_brk(k,:) = randbreaks();end% Select the Colors for the Plotted Routesclr = [1 0 0; 0 0 1; 0.67 0 1; 0 1 0; 1 0.5 0];if salesmen > 5 clr = hsv(salesmen);end% Run the GAglobal_min = Inf;total_dist = zeros(1,pop_size);dist_history = zeros(1,num_iter);tmp_pop_rte = zeros(8,n);tmp_pop_brk = zeros(8,num_brks);new_pop_rte = zeros(pop_size,n);new_pop_brk = zeros(pop_size,num_brks);if show_prog pfig = figure('Name','MTSPF_GA | Current Best Solution','Numbertitle','off');endfor iter = 1:num_iter % Evaluate Members of the Population for p = 1:pop_size d = 0; p_rte = pop_rte(p,:); p_brk = pop_brk(p,:); rng = [[1 p_brk+1];[p_brk n]]'; for s = 1:salesmen d = d + dmat(1,p_rte(rng(s,1))); % Add Start Distance for k = rng(s,1):rng(s,2)-1 d = d + dmat(p_rte(k),p_rte(k+1)); end d = d + dmat(p_rte(rng(s,2)),1); % Add End Distance end total_dist(p) = d; end % Find the Best Route in the Population [min_dist,index] = min(total_dist); dist_history(iter) = min_dist; if min_dist < global_min global_min = min_dist; opt_rte = pop_rte(index,:); opt_brk = pop_brk(index,:); rng = [[1 opt_brk+1];[opt_brk n]]'; if show_prog % Plot the Best Route figure(pfig); for s = 1:salesmen rte = [1 opt_rte(rng(s,1):rng(s,2)) 1]; if dims == 3, plot3(xy(rte,1),xy(rte,2),xy(rte,3),'.-','Color',clr(s,:)); else plot(xy(rte,1),xy(rte,2),'.-','Color',clr(s,:)); end title(sprintf('Total Distance = %1.4f, Iteration = %d',min_dist,iter)); hold on end if dims == 3, plot3(xy(1,1),xy(1,2),xy(1,3),'ko'); else plot(xy(1,1),xy(1,2),'ko'); end for i=1:30 text(xy(i,1)+0.0002,xy(i,2),num2str(i)) ; %加上0.01使标号和点不重合,可以调整 end hold off end end % Genetic Algorithm Operators rand_grouping = randperm(pop_size); for p = 8:8:pop_size rtes = pop_rte(rand_grouping(p-7:p),:); brks = pop_brk(rand_grouping(p-7:p),:); dists = total_dist(rand_grouping(p-7:p)); [ignore,idx] = min(dists); best_of_8_rte = rtes(idx,:); best_of_8_brk = brks(idx,:); rte_ins_pts = sort(ceil(n*rand(1,2))); I = rte_ins_pts(1); J = rte_ins_pts(2); for k = 1:8 % Generate New Solutions tmp_pop_rte(k,:) = best_of_8_rte; tmp_pop_brk(k,:) = best_of_8_brk; switch k case 2 % Flip tmp_pop_rte(k,I:J) = fliplr(tmp_pop_rte(k,I:J)); case 3 % Swap tmp_pop_rte(k,[I J]) = tmp_pop_rte(k,[J I]); case 4 % Slide tmp_pop_rte(k,I:J) = tmp_pop_rte(k,[I+1:J I]); case 5 % Modify Breaks tmp_pop_brk(k,:) = randbreaks(); case 6 % Flip, Modify Breaks tmp_pop_rte(k,I:J) = fliplr(tmp_pop_rte(k,I:J)); tmp_pop_brk(k,:) = randbreaks(); case 7 % Swap, Modify Breaks tmp_pop_rte(k,[I J]) = tmp_pop_rte(k,[J I]); tmp_pop_brk(k,:) = randbreaks(); case 8 % Slide, Modify Breaks tmp_pop_rte(k,I:J) = tmp_pop_rte(k,[I+1:J I]); tmp_pop_brk(k,:) = randbreaks(); otherwise % Do Nothing end end new_pop_rte(p-7:p,:) = tmp_pop_rte; new_pop_brk(p-7:p,:) = tmp_pop_brk; end pop_rte = new_pop_rte; pop_brk = new_pop_brk;endif show_res % Plots figure('Name','MTSPF_GA | Results','Numbertitle','off'); subplot(2,2,1); if dims == 3, plot3(xy(:,1),xy(:,2),xy(:,3),'k.'); else plot(xy(:,1),xy(:,2),'k.'); end for i=1:30 text(xy(i,1)+0.0002,xy(i,2),num2str(i)) ; %加上0.01使标号和点不重合,可以调整 end title('Locations'); subplot(2,2,2); imagesc(dmat([1 opt_rte],[1 opt_rte])); title('Distance Matrix'); subplot(2,2,3); rng = [[1 opt_brk+1];[opt_brk n]]'; for s = 1:salesmen rte = [1 opt_rte(rng(s,1):rng(s,2)) 1]; if dims == 3, plot3(xy(rte,1),xy(rte,2),xy(rte,3),'.-','Color',clr(s,:)); else plot(xy(rte,1),xy(rte,2),'.-','Color',clr(s,:)); end title(sprintf('Total Distance = %1.4f',min_dist)); hold on; end if dims == 3, plot3(xy(1,1),xy(1,2),xy(1,3),'ko'); else plot(xy(1,1),xy(1,2),'ko'); end for i=1:30 text(xy(i,1)+0.0002,xy(i,2),num2str(i)) ; %加上0.01使标号和点不重合,可以调整 end subplot(2,2,4); plot(dist_history,'b','LineWidth',2); title('Best Solution History'); set(gca,'XLim',[0 num_iter+1],'YLim',[0 1.1*max([1 dist_history])]);end% Return Outputsif nargout varargout{1} = opt_rte; varargout{2} = opt_brk; varargout{3} = min_dist;end % Generate Random Set of Break Points function breaks = randbreaks() if min_tour == 1 % No Constraints on Breaks tmp_brks = randperm(n-1); breaks = sort(tmp_brks(1:num_brks)); else % Force Breaks to be at Least the Minimum Tour Length num_adjust = find(rand < cum_prob,1)-1; spaces = ceil(num_brks*rand(1,num_adjust)); adjust = zeros(1,num_brks); for kk = 1:num_brks adjust(kk) = sum(spaces == kk); end breaks = min_tour*(1:num_brks) + cumsum(adjust); end endend%代码参考:CSDN
[1]汤雅连,杨期江.求解旅行商问题的蚁群优化算法参数设计[J].东莞理工学院学报,2020,27(03):48-54.
[2]宋志飞. 基于蚁群算法的TSP问题研究[D].江西理工大学,2013.
[3]束东来. 基于遗传算法的多旅行商问题的优化[D].安庆师范大学,2018.
[4]CSDN,蚁群算法求解TSP问题,遗传算法求解MTSP问题
参考文献

学习笔记
微信号|我的头发可没乱
新浪微博|我的头发可没乱
版权声明:本文为weixin_39607240原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。