题目描述:
给你 n nn 个非负整数 a 1 a_1a1,a 2 a_2a2,…,a n a_nan,每个数代表坐标中的一个点 (i ii, a i a_iai) 。在坐标内画n nn条垂直线,垂直线i ii的两个端点分别为 (i ii, a i a_iai) 和 (i ii, 0) 。找出其中的两条线,使得它们与x xx轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器。
示例1:
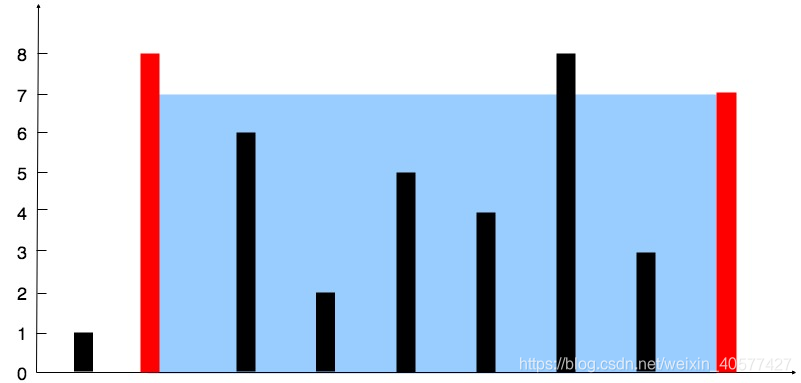
解题思路:
1、双指针:
这道题主要使用左右指针l e f t leftleft和r i g h t rightright,分别初始化为0 00和l e n − 1 len - 1len−1,计算出两个点(l e f t leftleft,a l e f t a_{left}aleft)和(r i g h t rightright,a r i g h t a_{right}aright)之间所能组成的最大容器面积,根据题意,面积a r e a = M a t h . m i n ( a l e f t , a r i g h t ) ∗ ( r i g h t − l e f t ) area = Math.min(a_{left},a_{right}) *(right - left)area=Math.min(aleft,aright)∗(right−left),然后更新最大面积。
更新l e f t 、 r i g h t left、rightleft、right指针的过程:
假设a l e f t < a r i g h t a_{left} < a_{right}aleft<aright,即a l e f t a_{left}aleft为较小的高度,这时更新l e f t leftleft:l e f t leftleft减一,否则更新r i g h t rightright:r i g h t rightright加一,这样不断重复上述过程,直至l e f t = = r i g h t left == rightleft==right。
以上的过程的正确性证明:
当固定较低的柱子a l o w a_{low}alow,移动较高一边的柱子a h i g h a_{high}ahigh,那么有两种情况:(1)遇到不比a h i g h a_{high}ahigh低的柱子;(2)遇到比a h i g h a_{high}ahigh低的柱子。这两种情况下容器的高度分别保持不变和变低,都一定不会变高(这是因为容器的高度取最低的那根柱子),而宽度一定减少,所以水的面积一定减少。因此只有移动较低的柱子才有可能出现较大的面积。
时间复杂度和空间复杂度: 时间复杂度为 O ( N ) O(N)O(N) ,空间复杂度为O ( 1 ) O(1)O(1)
实现代码:
public int maxArea(int[] height) {
if(height == null)
return 0;
int res = 0, len = height.length;
int left = 0, right = len - 1;
while(left < right){
int area = (right - left) * Math.min(height[left], height[right]);//计算面积
res = Math.max(res, area);//更新最大面积
if(height[left] < height[right])//移动较低的柱子
left++;
else
right--;
}
return res;
}