复杂度分析

空间复杂度S(n)

根据算法写成的程序在执行时占用存储单元的长度。这个长度往往与输入数据的规模有关。空间复杂度过高的算法可能导致使用的内存超限，造成程序非正常中断。

时间复杂度T(n)

根据算法写成的程序在执行时耗费的时间长度。这个长度往往也与输入数据的规模有关。时间复杂度过高的抵消算法可能导致我们在有生之年都等不到运行结果。

复杂度分析

在分析一般的算法效率时，一般关注两种复杂度

最坏情况复杂度$$T_{worst}(n)$$
平均复杂度$$T_{avg}(n)$$

若两段算法分别有复杂度$$T_1(n)=O(f_1(n))$$和$$T_2(n)=O(f_2(n))$$，则
$$T_1(n)+T_2(n)=max(O(f_1(n)),O(f_2(n))$$
$$T_1(n)\ast T_2(n)=O(f_1(n)\ast f_2(n))$$
若T(n)是关于n的k阶多项式，那么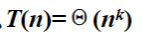

一个for循环的时间复杂度等于循环次数乘以循环体代码的复杂度

if-else结构的复杂度取决于if的条件判断 复杂度和两个分支部分的复杂度，总体复杂度取三者中最大