Sunday 模式匹配算法

Sunday算法是Daniel M.Sunday于1990年提出的一种比BM算法搜索速度更快的算法。该算法的核心思想是:在匹配过程中，模式串并不被要求一定要按从左向右进行比较还是从右向左进行比较， 它在发现不匹配时， 算法能跳过尽可能多的字符以进行下一步的匹配，从而提高了匹配效率。

相对于KMP算法与BM算法原理复杂不易实现， Sunday算法原理简单执行速度快。本文介绍下该算法的实现，以及该算法一些的改进。

原理：

假设在发生不匹配时T[i] ≠ P[j](0≤i<N, 0≤j<m)， 此时已经匹配的部分字串问为u,并假设子串u的长度为L.如下图.

这时，我们可以知道T[L+i+l]肯定要参加下一轮的匹配，因为P[m-1]至少要移动到这个位置( 即模式串P至少向右移动一个字符的位置).

下面有两种情况:
1、T[L+i+1]在模式串P中没有出现:

这个时候模式申P移动到T[L+i+1](包括T[L+i+1]本身)之前的任何位置,都没有意义.因此,P[0]必须移动到T[L+i+1]之后的字符的位置;如图：

2、T[L+i+1]有在模式串P中出现:
指T[L+i+1]从模式串P的右侧,按P[m-1],P [m-2]...P[0]的次序查找(字符在模式串中最右边出现位置)。如果发现T[L+i+1]和P中的某个字符相同,则记下这个位置,记为k(0 < k < m);如图：

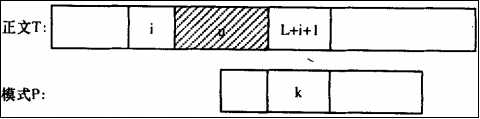
按照这种移动算法，然后按照字符从左向右的次序匹配。如果完全匹配了，则匹配成功；否则直接跳过，一直匹配到主串最右端；

下面是实现代码：

#include <stdio.h>		//printf()
#include <string.h>		// strlen()

#define ALPHABET_SIZE (1 << (sizeof(char)*8))

void calc_delta1(const unsigned char *needle, unsigned int nlen, int delta1[]) 
{
	unsigned int j = 0;
	for (j = 0; j < ALPHABET_SIZE; j++)
	{
		//if char not exist in needle, we can skip nlen+1
		delta1[j] = nlen+1;
	}

	for (j = 0; j < nlen; j++)
	{
		//与BM及BM Horspool坏字符规则不同，BM和BM Horspool算法里面的坏规则是 delta1[needle[j]] = nlen - 1 - j
		//因为比对的字符不同，就算和needle最后一个字符一样，也需要移动1个位置
		delta1[needle[j]] = nlen - j;
	}
}

void sunday_matcher(const unsigned char* haystack, unsigned int hlen,
                           const unsigned char* needle, unsigned int nlen)
{
	unsigned int haystack_index = 0, needle_index = 0;
	int *delta1 = NULL;

	delta1 = new int[ALPHABET_SIZE];

	calc_delta1(needle, nlen, delta1);

	while(haystack_index <= hlen-nlen)
	{
		while(needle_index < nlen)
		{
			if (haystack[haystack_index+needle_index] != needle[needle_index])
			{
				break;
			}
			
			needle_index++;
		}
	
		if (nlen == needle_index)
		{
			printf("needle occurs with shifts %d\n", haystack_index);
		}
	
		if(haystack_index+needle_index < hlen)
		{
			//printf("current haystack_index [%d], needle_index [%d]\n", haystack_index, needle_index);
			needle_index = 0;
			//步进取得是当前needle后面的那个字符，区别于BM及BM Horspool里面的坏字符规则
			haystack_index += delta1[haystack[haystack_index+nlen]];
		}
		else
		{
			break;
		}
	}

	delete [] delta1;
}

void main(void)
{
	char haystack[80] = "when you want to give ur, remember why you started";
	unsigned char needle[10] = "remember";

	sunday_matcher((const unsigned char *)haystack, strlen((const char*)haystack), \
							(const unsigned char*)needle, strlen((const char*)needle));
}

该算法最坏情况下的时间复杂度为O(n*m).对于短模式串的匹配问题，该算法执行速度较快；

同时我们可以发现Sunday算法有下面两个缺点：
1、没有有效利用前一次匹配结果(如KMP算法对前缀规则，和BM算法的后缀规则);
2、只利用主串下一个字符来遍历模式串的做法也过于简单，当模式串很长的时候，主串下一个字符在模式串中出现的概率会很高，会出现很多无效的匹配，降低效率；

改进：

针对1，我们可以引进KMP算法里面的好前缀规则，当然也可以参考BM的逆序进行匹配，利用BM的好后缀规则;
针对2，增加比对字符，在一次匹配后，用主串（haystack）后两个字符来遍历模式串，进行比较来确定模式串右移距离;
具体的算法大家可以自己实现下.

参考：

http://www.oschina.net/code/snippet_170948_12386

一种改进的字符串匹配算法

一种改进的sunday模式匹配算法