TOPSIS 法是一种常用的综合评价方法，其能充分利用原始数据的信息，其结果能精确地反映各评价方案之间的差距（ 层次分析法如果决策层大多，判断矩阵和一致矩阵相差会很大）

一、基本概念

TOPSIS 法是一种常用的综合评价方法，能充分利用原始数据的信息，其结果能精确地反映各评价方案之间的差距。

基本过程为先将原始数据矩阵统一指标类型（一般正向化处理）得到正向化的矩阵，再对正向化的矩阵进行标准化处理以消除各指标量纲的影响，并找到有限方案中的最优方案和最劣方案，然后分别计算各评价对象与最优方案和最劣方案间的距离，获得各评价对象与最优方案的相对接近程度，以此作为评价优劣的依据。该方法对数据分布及样本含量没有严格限制，数据计算简单易行。

Tip: 基本名词概念

• 极大型指标（效益型指标）：越大越好的指标

• 极小型指标（成本型指标）：越少（越小）越好的指标

• 正向化：将所有的指标转化为极大型

• 标准化：消去不同指标量纲的影响

• 归一化：将每一列数据转化为综合相加为1的数据类型（该数据值除以数据之和）

二、基本公式

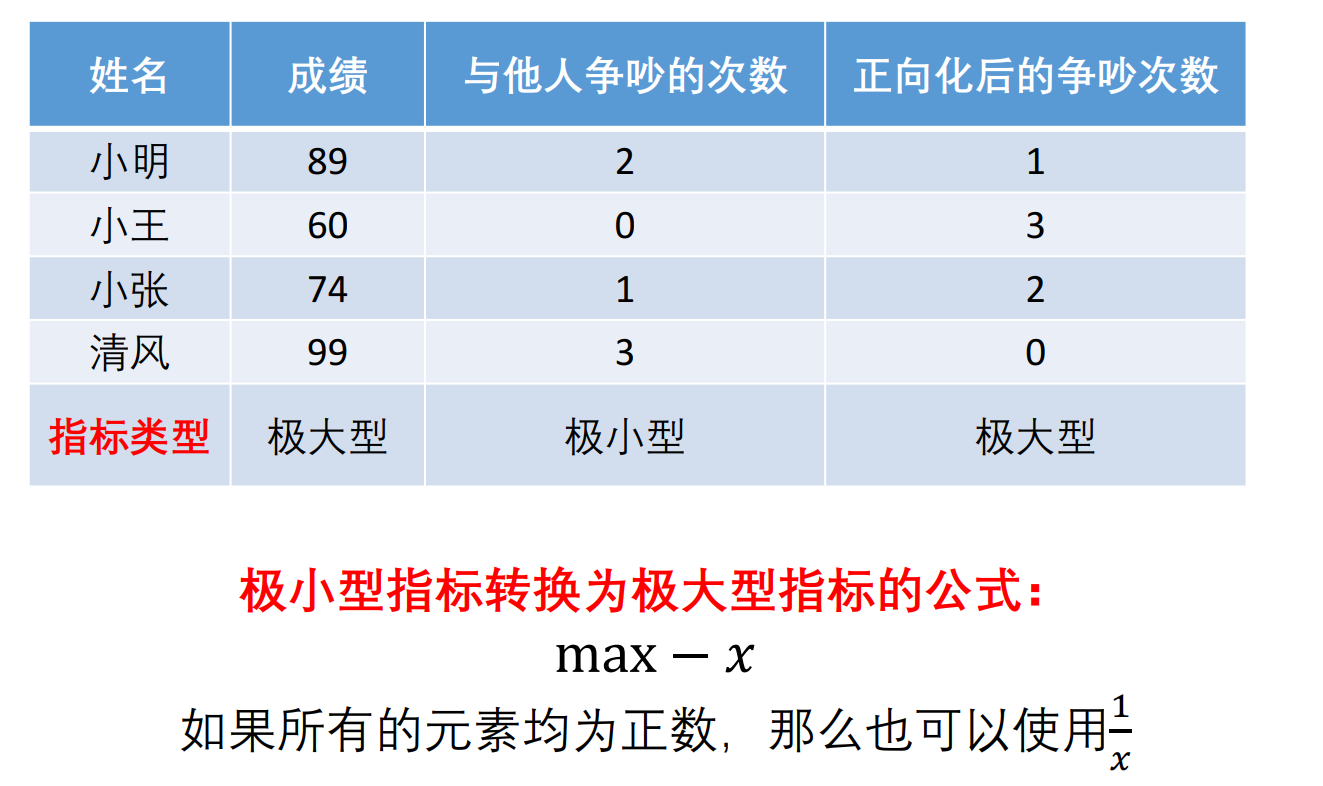
• 极小型指标转换为极大型指标的公式：max-x

• 标准化处理公式：

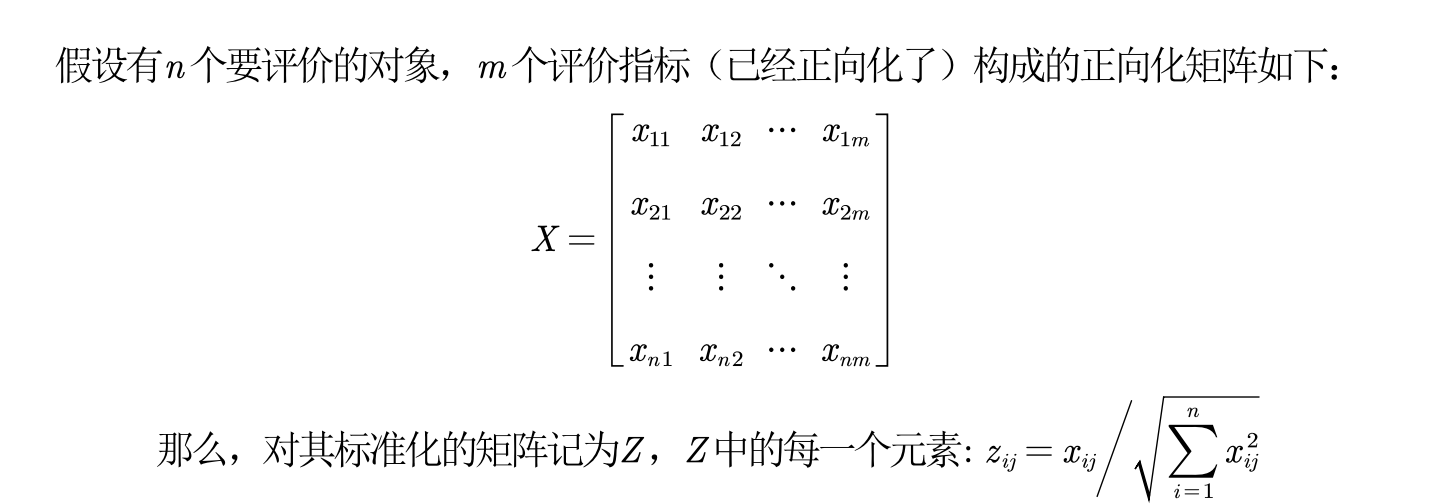
• 指标的分计算公式

三、实行步骤

1.将原始矩阵正向化

将所有的指标类型统一转化为极大型指标

(1).极小型指标 ->极大型指标

(2).中间型指标 -> 极大型指标

(3).区间型指标 -> 极大型指标

2.正向化矩阵标准化

注意：标准化的方法有很多种，其主要目的就是去除量纲的影响，未来我们还可能见到更多种的标准化方法，例如： (x‐x的均值)/x的标准差；具体选用哪一种标准化的方法在多数情况下并没有很大的限制，这里我们采用的是前人的论文中用的比较多的一种标准化方法。

3.计算得分并归一化

四、具体案例

请对以下几名同学进行评分

1.将原始矩阵正向化

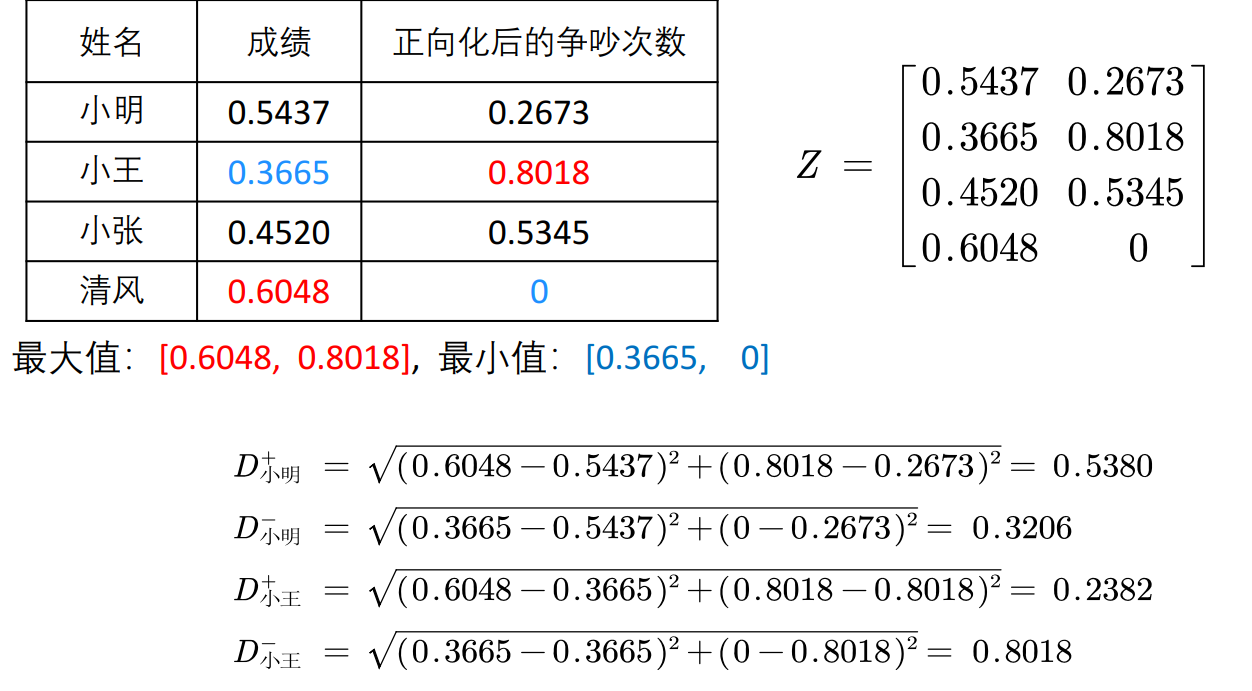
2.正向化矩阵标准化

3.计算得分并归一化