简单随机抽样
- 最基础的抽样方法
- 一次(非多层次、多阶段)抽样,或多阶段抽样的末端抽样(末端)总体的“要素”与抽样单位一致
简单随机抽样是抽样中最基本、最成熟、也是最简单的抽样设 计方式,是所有概率抽样方法发展、比较的基础。具体要求:
①熟练掌握简单随机抽样的抽样方式和样本抽选方法;
②熟知总体均值、总体总值和总体比例的简单估计;
③掌握样本量的确定;了解子总体的估计。
一.什么是简单随机抽样
定义:简单随机抽样(Simple Random Sampling, 简记为SRS)也称 纯随机抽样,对于大小为N的总体,抽取样本量为n的样本,若全部 可能的样本被抽中的概率都相等,则称这样的抽样为简单随机抽样.
分类:根据抽样单位是否放回可分为放回简单随机抽样和不放回简单随机抽样。
(一)放回简单随机抽样
定义:如果抽样是有放回的,每次抽取都是从
特点:(考虑与不考虑样本单位顺序)
共同点:同一个单位有可能在同一个样本中重复出现。
区别:(1)可能的样本数不同;(2)样本的概率分布不同,由此导致估计量的概率分布不同
(二)不放回简单随机抽样
定义:如果抽样是无放回的,即同一个单位不能在样本中重复出现,若考虑样本单位的顺序,则可能的样本为
若不考虑样本单位的顺序,则可能的样本为
共同点:(考虑与不考虑样本单位顺序)虽然可能的样本数不同,考虑顺序是不考虑顺序的n!倍,但是它们的样本有相同的概率分布。由此导致依据样本构造的估计量的概率分布也相同。
由于这一共同点的存在,加之不考虑顺序的放回简单随机抽样的工作量更小,所以抽样实践中对于不放回简单随机抽样,只讨论和使用不考虑顺序不放回简单随机抽样。
(三)放回与不放回简单随机抽样的比较
两者的主要不同之处:
- (1)每次抽取样本单位面对的总体结构不同。这一点使得前者 的数学处理相对简单。
- (2)样本提供的信息量不同。显然,在样本量一定的条件下, 由于后者提供的信息量大于前者,其抽样效率更高。
在实践中,一般多采用不考虑顺序的不放回简单随机抽样,所以 以下讨论如无特别说明,都指这一类简单随机抽样。
二、简单随机样本的抽选方法
简单随机样本的抽选,首先要将总体N个单位从1到N编号,每个单位对应一个号;然后从所编的号中抽号,如果抽到某个号,则对应的那个单位入样,直到抽够n个单位为止。
简单随机样本的抽选,通常有抽签法、随机数法。
(一)抽签法
当总体容量不大时,可分别采用两种方法抽取:
(1)全样本抽选法:即从N个签中一次抽取n个;
(2)逐个抽选法:即一次抽取一个签但不放回,接着抽下一个签, 直到抽够n个签为止。
可以证明,按这两种方法抽到的n个单位的样本是等价的,每个样 本被抽到的样本的概率都等于
(二)随机数法
当总体容量较大时,抽签法实施起来比较困难,这时可以 利用随机数表、随机数骰子、摇奖机、计算机产生的伪随机数 进行抽样。
1、利用随机数表抽样
随机数表是一张由0,1,2,…,9这十个数字组成的,一 般常用的是五位数的随机数字表,10个数字在表中出现的顺序 是随机的,每个数字都有同样的机会被抽中。
用随机数表抽选简单随机样本时,一般可根据总体容量N 的位数决定在随机数表中随机抽取几列。 比如N=768,要从中抽取N=10的简单随机样本,则在随机 数表中随机抽取相邻的3列,顺序往下(或往上),选出前10个 001到768之间的互不相同的数,如果这3列随机数字不够,可另 选其他3列继续,直到抽够个n单位为止。
用此种方法,当N的最高位数较小,比如小于5,且n不小时,由 读到的随机数被舍弃不用的比例较大,抽选效率较差。例如N=247, 此时采用下面的方法。
在随机数表中随机抽取3列,顺序往下,如果得到的随机数大于 247,小于989(因为247的4倍为988,因此000及989到999的数字应舍弃),则用这个数除以247,得到的余数入样,显然这种方法效率要高得多。随机数表的起始页和起始点都应用随机数产生。
2、利用随机数骰子抽样
3、利用摇奖机抽样
4、利用计算机产生的伪随机数抽样
大多数统计软件都有现成的产生随机数的程序。利用计算机产生 的随机数具有快捷、方便的特点。但通常产生的伪随机数有循环周期。 因此在有条件的情况下,一般不建议使用此种方法。
三、简单随机抽样在抽样理论中的地位与局限性
1,简单随机抽样在抽样理论中的地位
简单随机抽样在抽样理论中占有重要的地位,其他抽样方法都是在它的基础上发展起来的。它是抽样中最容易掌握的技术,也是发展最成熟的技术,建立了最完备的理论。简单随机抽样也是比较其他抽样设计方法优劣的基础。
2,简单随机抽样局限性
简单随机抽样也有许多局限性,其他抽样方法都是在它的基础 上,针对它的局限性发展起来的。当总体单位数N很大时,编制抽样框困难;抽样框中即使有辅助信息也不加利用,使得估计的统计效率较其他利用辅助信息的抽样设计方法低;由于样本在总体中的地理分布范围较广,如果采取面访,则费时、费钱、费力,困难较大;可能得到一个“差”的简单随机样本;若不用计算机,而用随机数表或随机数骰子抽取一个大样本,比较费力单调。
一、总体均值的简单估计
总体均值
(一)简单估计的定义
对于简单随机抽样,最简单的估计是利用样本均值作为总体均值的估计,即总体均值的简单估计量为:
也就是说,样本均值是总体均值的简单估计。
(二)简单估计的性质.
1、无偏性:对于简单随机抽样,样本均值
2、简单估计的方差:对于简单随机抽样,简单估计 的方差为
证明:
根据对称性论证法,有
3、简单估计
证明:
根据对称性论证法,有
由此可得:
例1 为调查某大学学生的电信消费水平,在全校N=15230名学生中,用简单随 机抽样的方法抽得一个n=36的样本。对每个抽中的学生调查其上个月的电信支出金额(如下表所示)。试以95%的置信度估计该校大学生该月电信消费的平均支出额。
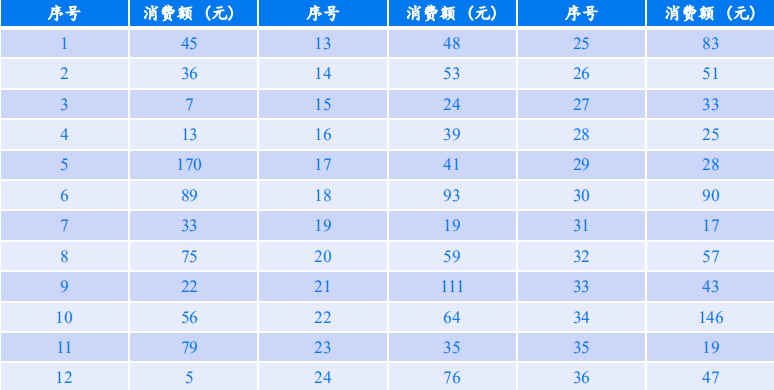
解:(1)点估计:依据题意和表中数据,计算可得
对该校大学生某月的电信消费的人均支出额的估计为53.64(元)。
(2)置信区间:
置信度95%对应的
二、总体总值的简单估计
总体总值
(一)简单估计的定义
定义:对于简单随机抽样,总体总值的简单估计是样本均值的N倍,即总体均值的简单估计量为:
(二)简单估计的性质.
1、无偏性:对于简单随机抽样,总体总值的简单估计是总体总 值的无偏估计,即有
证明:
2、简单估计的方差:对于简单随机抽样,总体总值的简单估计的方差为
例2
试以95%的置信度估计例1中该校大学生该月电信消费的总支出额,并给出在置信度95%的条件下,估计的极限相对误差。
解: (1)点估计:依题意,N=15230,根据例1计算的结果,可估计该校大 学生该月电信消费的总支出额为
(2)置信区间:
以95%的把握估计该校大学生该月电信消费的总支出额为:
816 937.2±1.96×93 443.71元,即在[633787.53, 1000086.87]元之间。
(3)在置信度95%下,
一,问题的提法
除了总体均值和总体总值外,总体中具有某种属性的单位占总体单位的比例也是经常需要估计的总体指标之一。
例如要估计规模以上工业企业占全部工业企业的比例;估计 某大学女教授占全部教授的比例;研究年龄大于等于65岁人口的 比例等等。
设
设总体中有N 个单位,具有某种属性的单位数为
总体中具有某种属性的单位比例为:
总体中不具有该种属性的单位的比例为:
结论:对总体比例的估计就是对总体均值的估计,对总体中具有某 种属性单位的总个数的估计就是对总体总值估计的一个特例。
二,总体比例的简单估计量及其性质
简单估计量的定义
根据调查要求,利用简单随机抽样的方式随机抽取n个单位组成样本, 其中
就是总体比例
就是总体中具有某种属性单位的总个数 的简单估计量。
总体方差:,有个单元具有A这个特征时
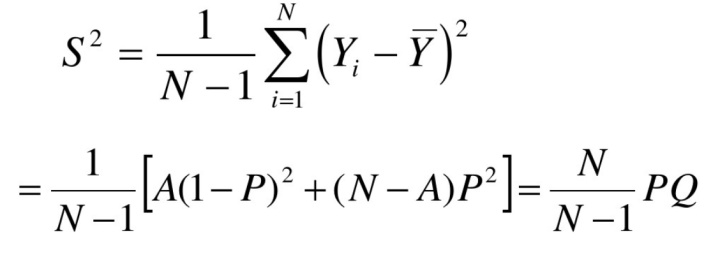
估计量的性质
(1) p是P的无偏估计。即有
(2) p的方差为:
(3)
(4) 当N, n, N-n都比较大时,P的置信度为
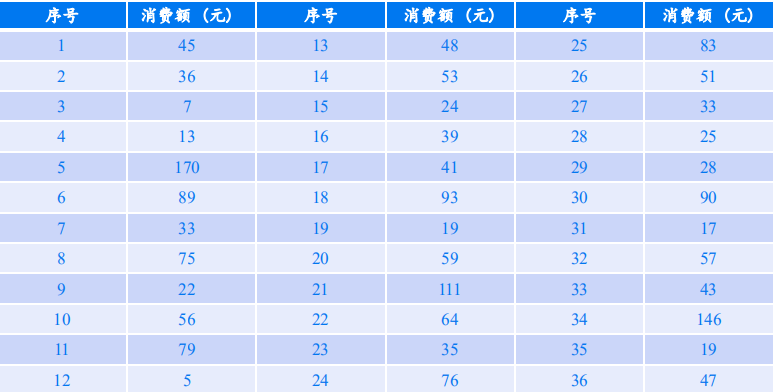
例1 为调查某大学学生的电信消费水平,在全校N=15230名学生中,用简单随机 抽样的方法抽得一个n=36的样本。对每个抽中的学生调查其上个月的电信支出金 额(如下表所示)。试以95%的置信度估计该校大学生该月电信消费支出超出80 元的人数及其比例。

一、确定样本量主要考虑的因素
在抽样调查的理论方法研究中,样本量的确定既有重要的理论意义, 又有现实的实用价值。 样本量的确定主要受两个方面因素的影响:
(1)对抽样估计量精度的要求。总体单位调查标志的变异程度、总体 的大小、样本设计和所使用的估计量、回答率等都是影响样本量的因素。
(2)实际调查运作的限制。调查的经费、允许的调查时间、调查人员数量等都是影响样本量的因素。另外还有些限制因素在样本量的计算公式中还无法体现,但是在确定最终所需的样本量时必须加以考虑。
在实际工作中常采用两种不同的方式来确定:
(1) 在总费用一定的条件下,使精度最高;
(2) 在满足一定精度要求的条件下,使费用最小。
精度margin of error
对精度的要求通常以允许最大绝对误差d (绝对误差限)或允许最大相对误差r(相对误差限)来表示。
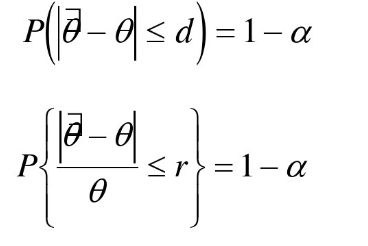
对于简单随机抽样,设费用为样本量的线性函数,即有:
式中,C为总费用;
如果总费用受到限制,固定费用与平均单位变动费用给定,最大的样本量
就确定了。
说明:抽样调查受抽样误差的影响,也受非抽样误差的影响。抽样调查估计量的精度是抽样误差大小的度量,抽样误差是由于随机抽样而不是由于具体调查而产生的。确定样本量是为控制抽样误差,而不是对非抽样误差进行控制。
对于简单随机样本,样本量n与估计量精度的关系,可由估计量的概率意义上的绝对允许误差
或变异系数
由于
二、估计总体均值(总值)的样本量确定
给定估计量方差上限,样本量的确定
在简单随机抽样简单估计的情形下,根据样本均值y的方差公式
说明:
(1)在无限总体或放回抽样情形下,
(2)对于不放回简单随机抽样,若总体容量N很大,比如
(3)若N不很大,则用上述(*)式确定样本量n。
给定绝对允许误差
由于总体方差
例1
为调查某大学学生的电信消费水平,在全校N=15230名学生中,用简单随机 抽样的方法抽取样本。如果要求以95%的置信度估计该校大学生该月人均电信消费 支出的绝对允许误差不超过5元,样本量应确定为多少?

三、估计总体比例的样本量确定
给定估计量方差上限,样本量的确定
如果估计的是总体中具有某种属性的单位所占的比例
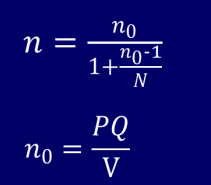
给定绝对允许误差
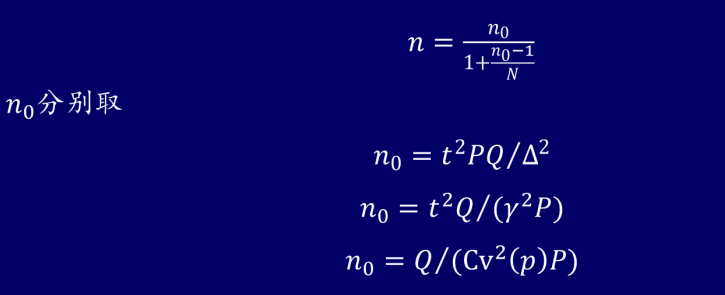
由于总体比例P未知,因此在利用上述公式时,必须事先对做出估计
例2
为调查某中学学生的每月购书支出水平,在全校名学生中,用不放回简单随机抽样的方法抽得一个的样本。对每个抽中的学生调查其上个月的购书支出金额
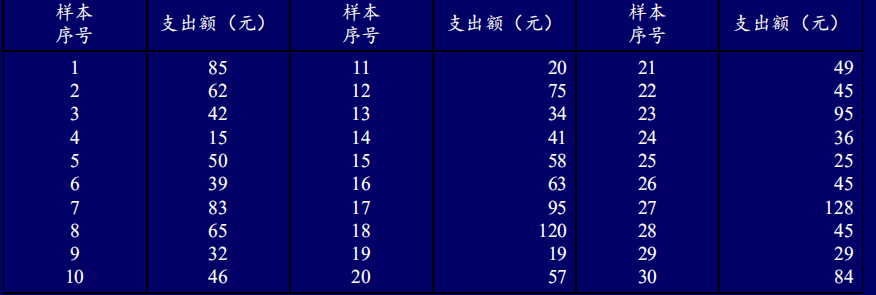
(1)在95%的置信度下估计该校学生该月平均购书支出额;
(2)试估计该校学生该月购书支出超出70元的人数;
(3)如果要求相对误差限不超过10%,以95%的置信度估计该校学生该月购书支出超 出70元的人数比例,样本量至少应为多少?
解: (1)依据题意和上表的数据,有
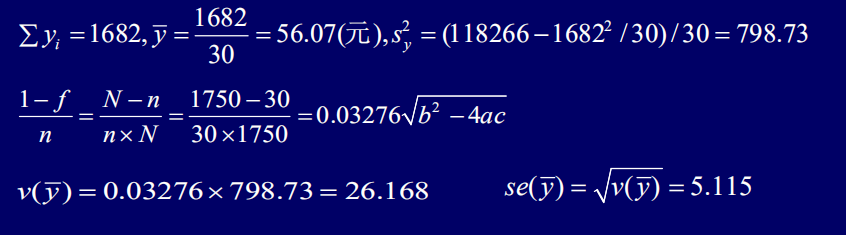
因此,对该校学生某月的人均购书支出额的估计为56.07元,由于置信度95%对应的
(2)易知,N=1750,n=30,
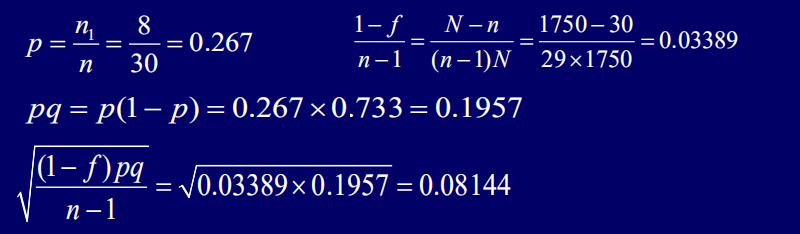
P的95%的置信区间为:

(3) N=1750,n=30,
由此可计算得:
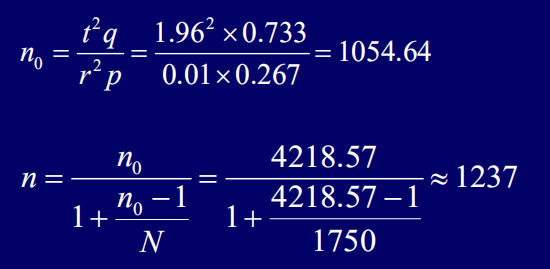
计算结果说明,至少应抽取一个样本量为1237的简单随机样本,才能满足95%置信度条件下相对误差不超过10%的精度要求。
●应用情景
- 通常,总体规模不大,总体、研究总体、抽样框,三者通常合一
- 内部的异质性没有大到需要专门处理的程度,即不需要分层
- 对总体要素的已知信息不多
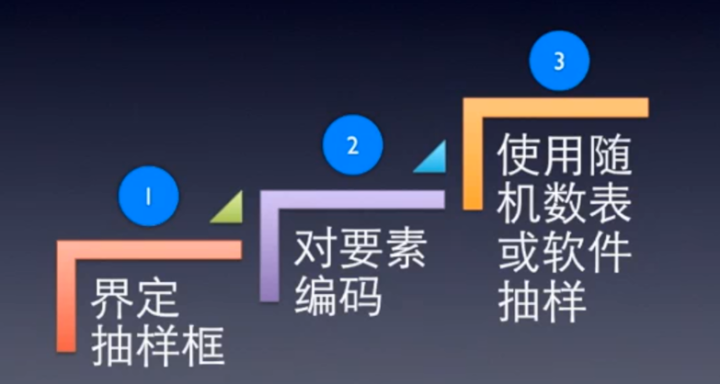
抽样步骤
定义:简单随机抽样的样本估计量的方差与复杂抽样的样本估计量的方差的比率。

设计效果:比较不同抽样方法的效率.
Deff的作用:
(1)评价抽样设计的--个依据,
如果deff<1,则抽样设计比简单随机抽样的效率高;
如果deff> 1,则抽样设计比简单随机抽样的效率低。
(2)计算样本量
如多阶段抽样的Deff大约在2~2.5之间。
n= n'(deff)
n'为简单随机抽样所需样本量。
放回简单随机抽样的deff为:
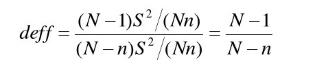
常用于复杂抽样样本量的确定;在一定精度条件下,简单随机抽样所需的样本量比较容易得到,复杂抽样的样本量为:
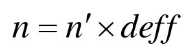
如果估计的是非常稀有事件的比例,这时总体比例很小,用极限相对误差比极限绝对误差更好些。
对于稀有事件,所需的样本量会很大,例
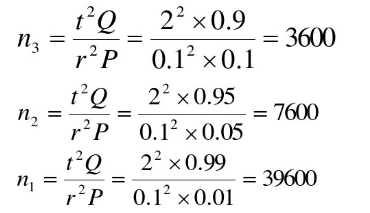
针对稀有事件并无法给出确切范围,
■对总体比例事先不同的假定,所导致的样本量差异非常大。
霍丹(Haldane) 提出的逆抽样方法:即事先确定-一个整数m (m>1),, 进行逐个抽样,直到抽到m个所考虑特征的单元为止.
设n是实际的样本量,则P的一个无偏估计为
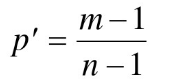


抽样方法
例子:一个30人班级的课堂提问
放回抽样
每个人都有被问到的机会,被问过的人,被放回到抽样框,因此,有被第二次问到的机会
非放回抽样
每个人都有被问到的机会,被问过的人,不再放回到抽样框,因此,没有被第二次问到的机会
问题
每个人被抽到的机会是等概率的吗?
运用随机数表进行抽样
制备抽样框
- 第一步:确定样本班级
- 第二步:将30名学生进行顺序编码,从00... .到29
使用随机数表抽样
- 第三步:随机选择起始点。在查阅随机数表之前,说出行、列起点
- 第四步:找到.上述起点,如希望抽取10名学生,就取I组随机数的固定位置,10名学生,即0-9,只需I位数。按照事先制定的规则,选中随机数字组中的I位,就是第一个样本,依事先规定的阅读方向,查到下一组数中的相同位置,就是第二个样本,依次类推
操作方法
制备抽样框(以CGSS为例)
- 第一步:将样本家庭户中所有符合“要素”资格的成员,按照规则顺序编号,如依据性别和年龄顺序或逆序排列
使用Kish表,通常用于末端抽样
- 第二步:拿出事先准备好的Kish表,根据其指引,抽选样本