开始今天的内容之前,需要大吼一声放假啦!感恩节假期正式开始,并且为防止节假日人流带来的更严重的新冠传染,感恩节之后本学期所有的课程也都将转为线上,也就是说,直到春季学期开学,我都会蜗居在自己的公寓里。来美国那么久,除了学校所在的城市,都没去过其他地方。本来今年暑假打算出游,可惜被疫情打乱,真希望疫情能早点过去。
回到我们的计量话题,今天要讲的内容是bootstrap自抽样。我还记得我在统计课上第一次学bootstrap的时候,全程都在神游,以至于后来做作业时以为bootstrap是什么特别高级难懂的技术问题,很长一段时间内碰到bootstrap就头大。但是后来重新复习的时候,发现bootstrap不过是一个非常简单的重复抽样过程,无非是使用R语言执行相关命令符的时候稍微有那么一点点复杂。如果仅仅局限于线性回归,那么Stata的bootstrap命令符使用就会简单很多。
在之前关于渐近性的推送中,我们有提到过,如果样本容量足够大的话,我们认为渐近性分布接近正态分布,也就满足了关于线性回归的正态分布的重要假设。但是,如果我们的样本容量没有那么大,没办法满足渐近性的要求,那又该怎么办呢?这时候bootstrap就是一个很有用的替代方法,bootstrap本质就是对现有的样本进行重复抽样得到新样本,以这种方法来模拟扩大样本容量。bootstrap的适用范围不仅限于线性回归估计,任何统计学里的估计量都可以通过bootstrap进行量化并且计算standard error标准误。并且我们完全不用在意估计量是否呈正态分布,通过bootstrap进行重复抽样,当重复样本足够多的时候,我们就可以模拟出估计量的分布状态。
bootstrap
bootstrap的基本理论
在前文介绍中我们已经提到,bootstrap本质就是对样本自身的重复抽样。我以一个非常简单的例子来进行解释,我们都知道扔硬币任意一面朝上的概率为0.5,假设我们有一枚硬币,我们随机扔10次,扔100次,扔1000次,随着次数的增多,那么其中一面朝上的概率会越来越接近0.5。假如我们没办法扔那么多次,比如只能扔10次,得出的概率值很大可能不等于0.5,如果我们想知道根据这10次计算出来的概率的误差有多少,应该怎么办呢?渐近性肯定是没办法用了,只有10次,样本容量太小。这时就我们就可以利用bootstrap,我们将这10次的结果记录下来,正面朝上为1,反面朝上为0。之后,我们对样本进行重复抽样,容量仍为10,因为是重复抽样,这10个结果中有的结果可能被抽出来两次甚至多次。第一次重复抽样得到一个新的样本,计算正面朝上的概率值;第二次重复抽样得到一个新的样本,计算正面朝上的概率值;第三次重复抽样得到一个新的样本,计算正面朝上的概率值;一直到第次,计算正面朝上的概率值。将通过重复抽样得到的估计值按照大小从低到高排列,假如我们想要获得95%置信区间,那么我们只需掐头去尾,去掉序列中前2.5%以及后2.5%的估计值,剩下的就是我们的置信区间。比如我们重复了1000次,那么95%的置信区间,从左往右数第25个以及从右往左数第25个就是分位数。我们也可以绘制分布直方图以及密度图,查看估计值的分布形态。下图是我的统计学老师的笔记中解释bootstrap流程的图:
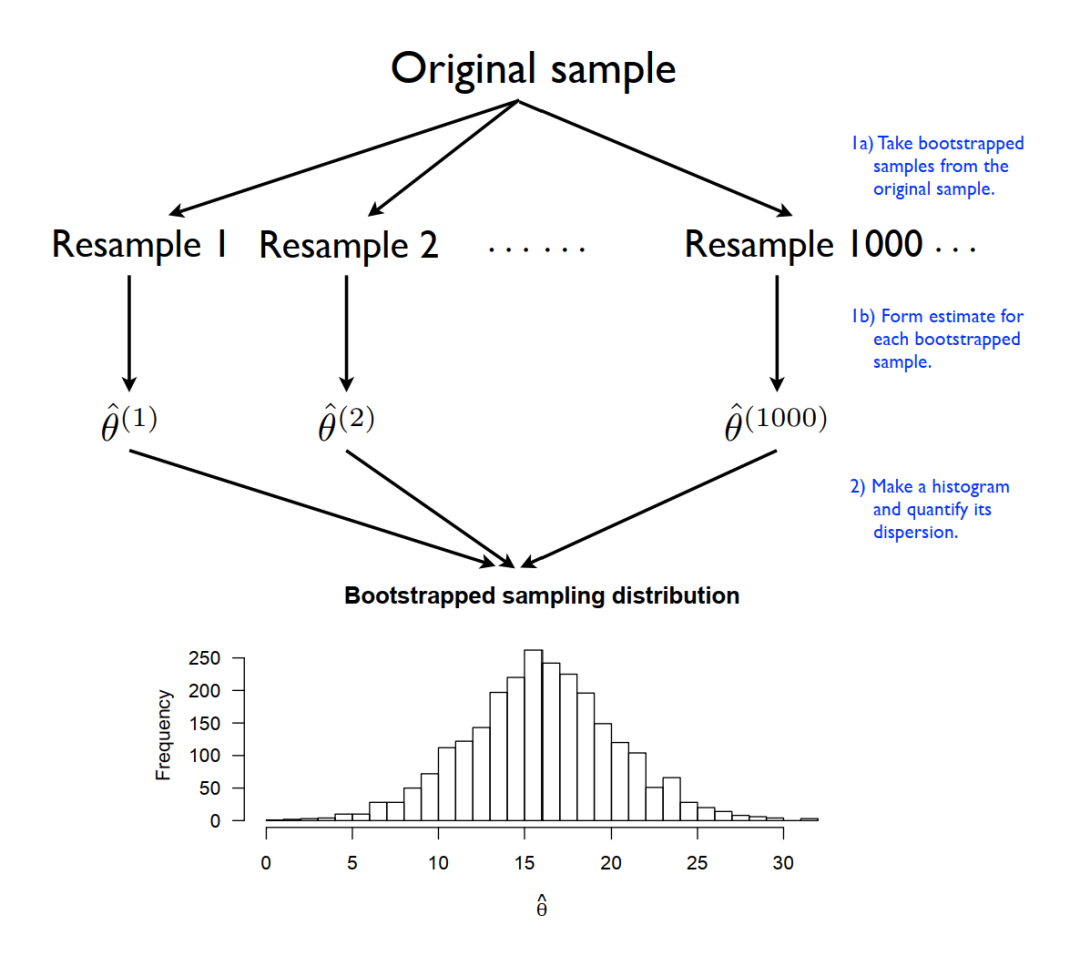
回到线性回归分析,假如我们想要获得回归系数的bootstrap standard error,那么我们只需对样本进行重复抽样,每次对重复抽样获得的样本进行一次回归,就可计算出一个回归系数估计值,而后不断进行重复抽样,假如进行1000次,我们就会获得1000个回归系数的估计值,使用standard error的计算公式,我们就可以计算出bootstrap standard error:
因为任何一个统计学的估计量都可以通过bootstrap进行量化,那么线性回归分析中的任何估计值我们都可以使用bootstrap,比如R方。
R语言手动实现bootstrap
在R语言中实现bootstrap稍稍有点难度,一般使用boot工具包执行相关的命令符,之所以有点难,是因为要先自己编写新的符合条件的命令符。我们先手动模拟下刚才我们所说的扔硬币过程,然后再介绍如何使用boot工具包的命令符:
### 加载工具包
library(tidyverse)
### 加载boot工具包
library(boot)
### 设定种子
set.seed(123)
### 生成10个硬币样本
coin 0, 1), size = 10, replace = TRUE)
### 计算平均值 也即正面朝上的概率 结果为0.4
mean(coin)

### 生成空白向量 填充bootstrap样本的平均值
bootstrap ### 重复抽样1000次 得到1000个估计值
for(i in 1:1000){
b 1:10), size = 10, replace = TRUE)]
bootstrap[i] }
### 计算bootstrap估计值的平均值
mean(bootstrap)

通过bootstrap样本得到的估计值的平均值为0.3916,和原始样本的估计值0.4非常接近。下面根据公式计算standard error:
sqrt(sum((bootstrap - mean(bootstrap))^2)/999)

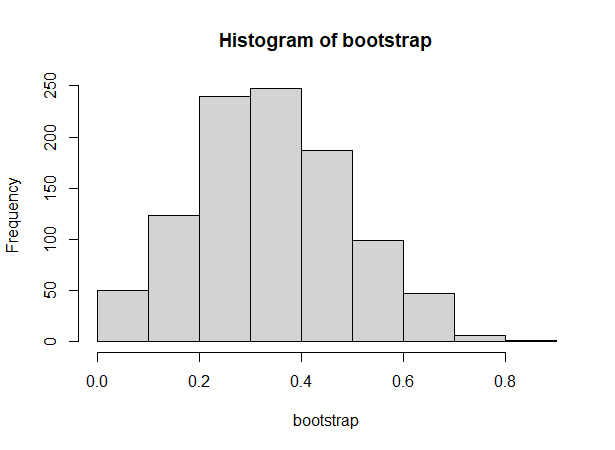
bootstrap计算得出的standard error约为0.152,也就是说,如果从总体中随机抽取一个容量为10的样本,我们认为该样本的平均值和其真实值之间的偏差约为0.152。这里我们知道硬币朝上的概率为0.5,样本的估计值为0.4,而bootstrap估计的样本估计值和0.5的偏差约为0.152。我们也可查看bootstrap重复抽样估计值的分布:
hist(bootstrap)
boot工具包
boot是比较常用的计算bootstrap的工具包,核心命令符为boot()和boot.ci()。第一个命令符就是用来执行bootstrap自抽样,第二个命令符用来计算bootstrap置信区间。
命令符boot()有三个最基本的参数。第一个参数data是告诉R对哪一个样本进行重复抽样;第三个参数R告诉R重复抽样多少次。注意这里第二个参数statistic输入的值必须是一个新的命令符,这个命令符能够生成一个估计量的值或者多个估计量的数字向量,并且这个命令符必须包括两个参数,第一个参数是样本数据,第二个参数是筛选样本。如果没有这两个参数,命令符boot()就没办法对原始样本进行重复抽样并进行估计。下面我们以刚才扔硬币的例子为例:
### 设置新的命令符 至少包括两个参数
### 其中一个表示样本数据
### 第二个参数表示筛选样本
### 新定义的函数就是对原始样本重新抽样然后计算平均值
### 结果为单个数字
coin_mean function(data, index){
b return(mean(b))
}
### 只要我们输入相应的参数值 上述命令符是可以单独运行的
coin_mean(data = coin, index = sample(1:10, 10, TRUE))

### 使用boot()命令符执行bootstrap
boot1 1000)
boot1
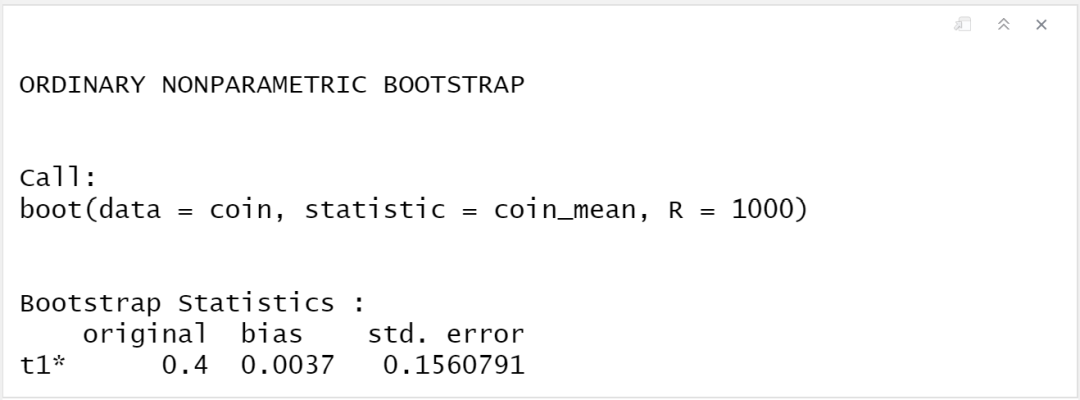
上图中的结果,其中original是指原始样本估计的平均值,我们最开始就已经知道是0.4,bias是指通过bootstrap得到的1000个估计值的平均值和原始样本平均值之间的差值,等下我们可以进行验证。std.error就是我们求出的标准误约为0.156。注意因为抽样是随机的,所以结果和我们刚才手动计算出来的不一样。这里命令符生成的结果是以list形式保存的,我们可以查看结果中都包括什么:
attributes(boot1)

这里面的t0是指原始样本估计的平均值,t是指通过bootstrap得到的那1000个估计值,以矩阵形式保存,这里为的矩阵。刚才我们说bias是这1000个估计值的平均值与t0的差值,我们可以手动验证:
### 查看矩阵
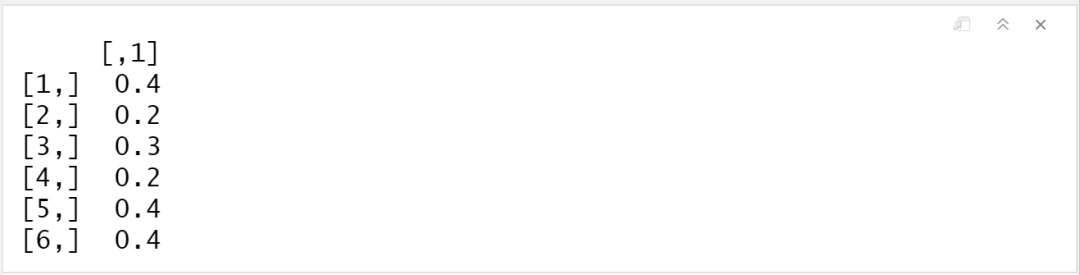
head(boot1$t)
### 手动计算bias
mean(boot1$t[,1]) - boot1$t0

R语言自带的plot()函数可以直接查看bootstrap估计值的分布以及检验其正态分布的QQ plot:
plot(boot1)
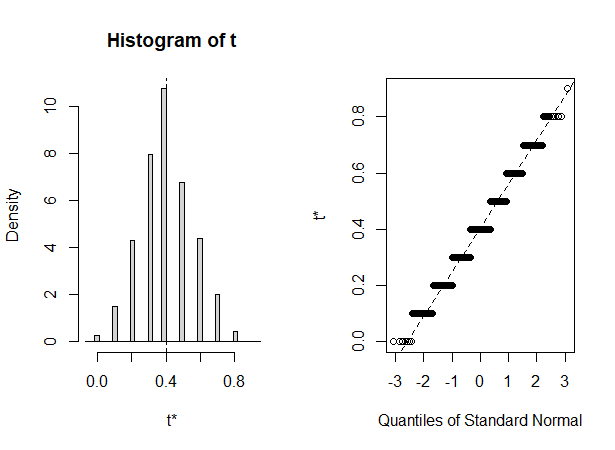
QQ plot是用来检验数据是否呈现正态分布的,横坐标是正态分布的分位数,纵坐标是样本数据分布的分位数,如果样本数据为正态分布,其分位数和正态分布的分位数一一对应,那么所有的点连在一起我们就可以看到一个45度斜向上的线。
使用boot.ci()可以查看bootstrap估计的置信区间:
### 这里参数type设定的值为percentile
### perc计算的置信区间就是前文所讲述的寻找置信区间的方法
### 除此之外命令符还提供其他类型的置信区间
### 感兴趣的可以看命令符的帮助页面
boot.ci(boot1, type = "perc")

下面我们用boot命令符来对线性回归进行检验。我们使用R自带的数据mtcars进行演示。回归的因变量为mpg每英里耗油量,自变量为wt车重和disp汽车排量。假设我们要计算回归系数的bootstrap standard error,首先写新的命令符,这个命令符能够返回估计的系数值:
### 这里的函数有三个参数值 同样至少有两个参数
### 其中一个是样本 另外一个是筛选样本
lmcoef function(data, index, formula){
### 对样本数据进行重复抽样
b ### 线性回归估计
lm1 ### 返回系数估计值
return(coef(lm1))
}
### 验证新的函数可以使用 返回数字向量
lmcoef(mtcars, index = sample(1:nrow(mtcars), size = nrow(mtcars), replace = T), mpg ~ wt + disp)

### 使用boot()执行bootstrap
### 注意刚才新写的命令符里面的参数formula这里要输入对应的参数值
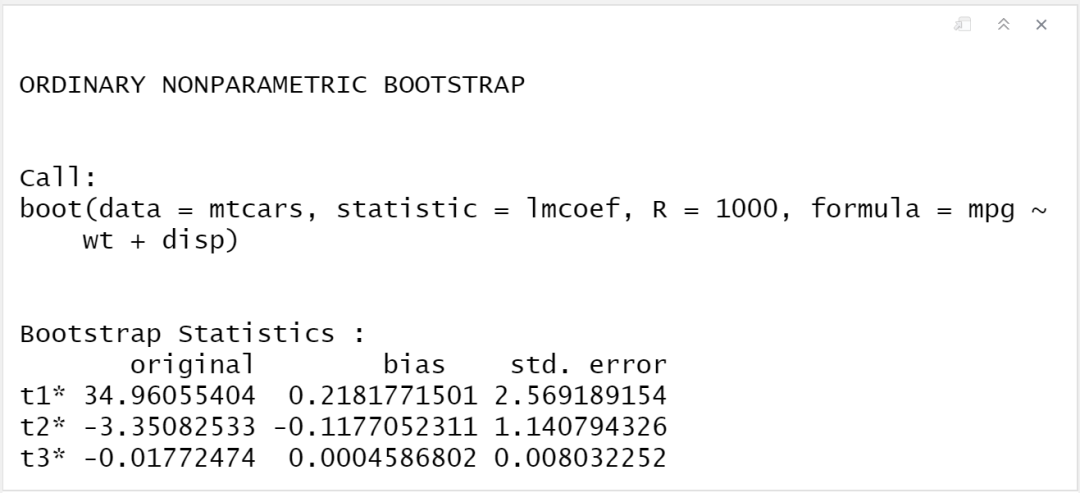
boot2 1000, formula = mpg ~ wt + disp)
boot2
head(boot2$t)
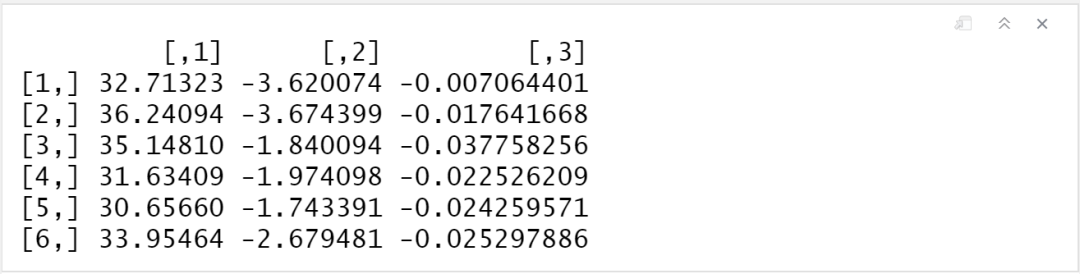
因为我们估计的系数值有三个,所以bootstrap给出的结果也有三个,和刚才命令符lmcoef()返回的向量里面的结果排列顺序一致。t1*就是(Intercept),t2*就是wt,t3*就是disp。此时结果里面保存的t应该是的矩阵,因为我们重复了1000次,估计了3个变量,矩阵中每一列均为该变量的1000个估计值。我们依旧可以使用plot()查看bootstrap的分布图,因为这时有三个估计值,所以我们添加一个新的参数index,1代表t1*,2代表t2*,3代表t3*。如果不给参数index设置值,会默认返还t1*的结果。假如我们想查看disp的分布图:
plot(boot2, index = 3)
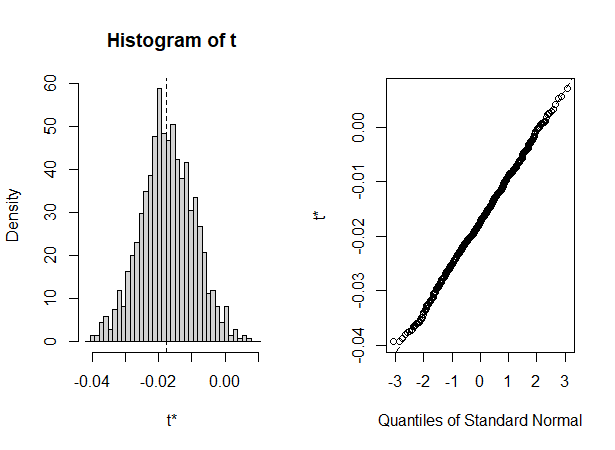
计算回归系数的置信区间,同理,需要输入index参数值,假如我们想要查看wt的置信区间:
boot.ci(boot2, type = "perc", index = 2)

假如我们想要计算R方的bootstrap标准误,我们只需写一个能够返回R方的命令符然后再用boot()执行即可:
lmrsquared function(data, index, formula){
b lm1 return(summary(lm1)$r.squared)
}
boot3 1000, formula = mpg ~ wt + disp)
boot3
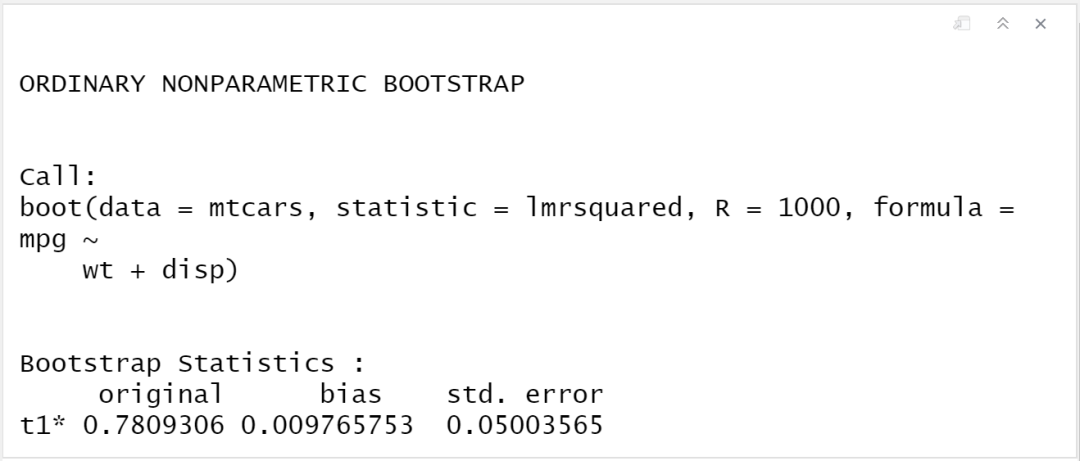
boot.ci(boot3, type = "perc")

在上述所有的bootstrap估计中,我都将重复抽样次数设置为1000,这是因为对于使用percentile计算置信区间的方法,1000次重复抽样才能够给出足够多的数据模拟结果。Stata默认的重复抽样次数为50,这对于假设的正态分布估计已经足够。最后,简要讲下如何在Stata中对线性回归进行bootstrap重复抽样估计:
### 使用Stata自带的auto.dta数据
sysuse auto
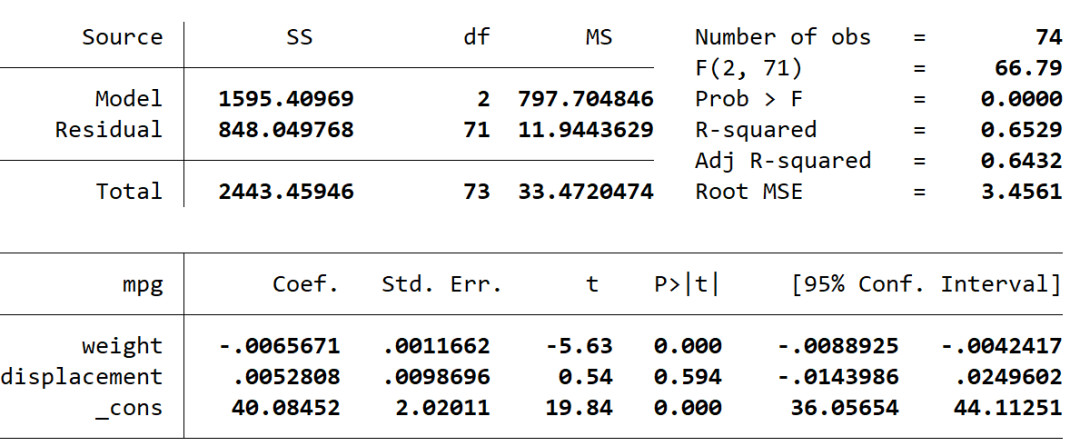
### 假设同方差进行回归
regress mpg weight displacement
### bootstrap
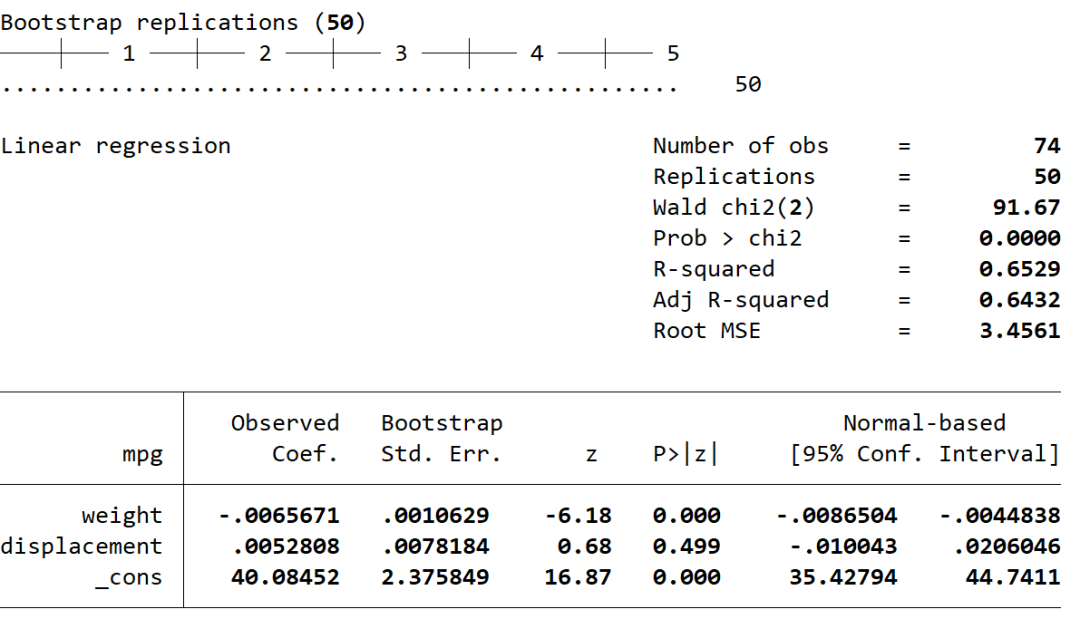
### 皆为默认50次
### 可以直接在回归命令符后面添加参数 设置bootstrap standard error
regress mpg weight displacement, vce(bootstrap)
### 也可以通过bootstrap命令符
bootstrap: regress mpg weight displacement
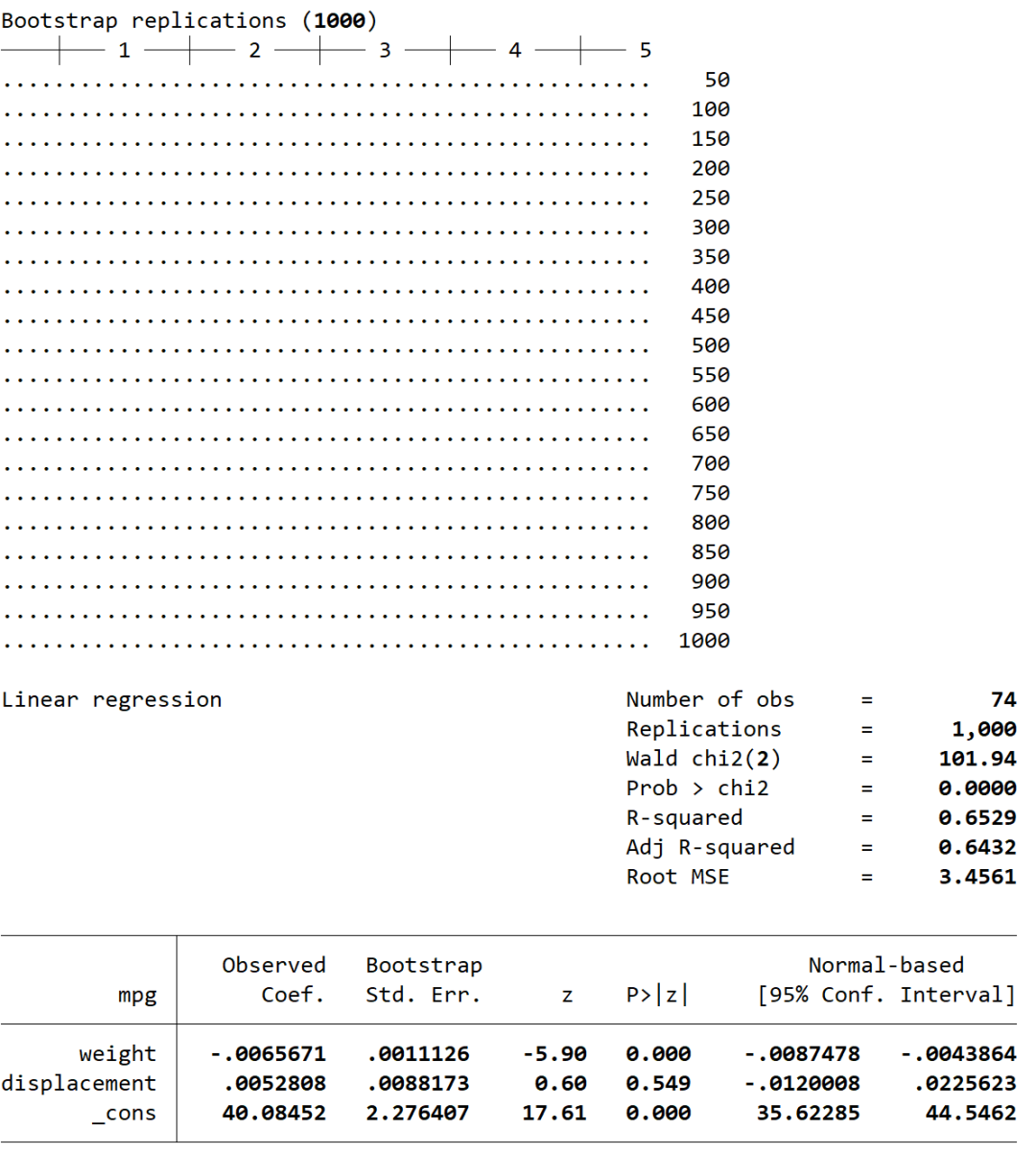
### 重复抽样1000次
bootstrap, rep(1000): regress mpg weight displacement
以上,就是在R语言中执行bootstrap自抽样的相关简介。