接上一部分:https://blog.csdn.net/weixin_41999529/article/details/90318536
导论
利用给定的一组样本数据估计一个平稳随机信号的功率谱密度称为功率谱估计。在许多工程应用中,功率谱的分析与估计是十分重要的,因为它能给出被分析对象的能量随频率的分布情况。例如在生物医学工程中,功率谱密度的峰形和波形显示类癫痫病发作的周期。
经典功率谱估计参看:https://mp.csdn.net/postedit/89642593
三、ARMA谱估计
4、AR参数估计的总体最小二乘法
一旦AR阶数p确定,如何求出p个AR参数的估计值呢?如果利用最小二乘方法,会带来两个问题:其一,必须重新列出法方程组,使它只包含p个未知数;其二,求解Ax = b的最小二乘方法只认为b含有误差,但是实际上系数矩阵A也含有误差。因此,一种比最小二乘法更合里的处理方法应该同时考虑A和b二者的误差或扰动。
1)总体最小二乘方法(TLS)
令m*n 矩阵A的误差矩阵为E,向量b的误差向量为e,即考虑矩阵方程:
(A+E)x = b +e (3.4.44)
的最小二乘解。由于考虑了总体的误差,所以这种最小二乘方法称为总体最小二乘方法。

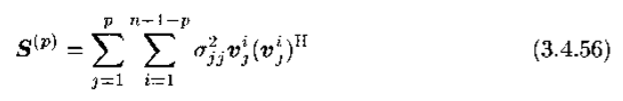
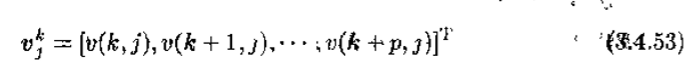
TLS方法的基本思想是使来自A和b的噪声扰动影响最小。

四、ARMA模型辨识
1、MA阶数确定

2、MA参数估计

五、最大熵谱估计
从信息论的观点介绍另一种功率谱估计方法——最大熵方法,这一方法是Burg于1967年提出的,由于最大熵的方法的一系列优点,它成为了现代谱估计的一个重要分支。最大熵谱估计在不同条件下与AR谱估计、ARMA谱估计之间存在着等价关系。
1、Burg最大熵谱估计


1)熵:
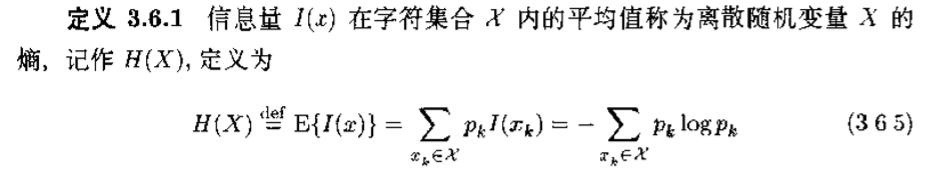


2)最大熵谱估计方法
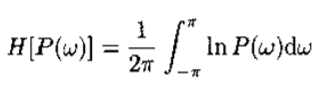 称为功率谱P(w)的熵(简称熵谱)。
称为功率谱P(w)的熵(简称熵谱)。

2、Levinson递推
3、Burg算法
4、最大熵谱估计和ARMA谱估计
六、Pisarenko谐波分解法
七、扩展Prony方法
八、多重信号分类(MUSIC)
九、旋转变技术(ESPRIT)
十、酉ESPRIT
申明:内容依据张贤达教授所著《现代信号处理》第二版所总结归纳