Poisson Equation

From Wikiversity

[hide]

1 Poisson's Equation

Poisson's Equation[edit]

Definition[edit]

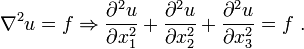
$\nabla^2 u = f \Rightarrow \frac{\partial^2 u}{\partial x_1^2} + \frac{\partial^2 u}{\partial x_2^2} + \frac{\partial^2 u}{\partial x_3^2} = f ~.$

Description[edit]

Appears in almost every field of physics.

Solution to Case with 4 Homogeneous Boundary Conditions[edit]

Let's consider the following example, where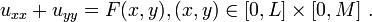 $u_{xx}+u_{yy}=F(x,y), (x,y) \in \lbrack 0,L \rbrack \times \lbrack 0,M \rbrack~.$ and the Dirichlet boundary conditions are as follows:

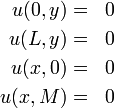
$\begin{align} u(0,y)&=&0 \\ u(L,y)&=&0 \\ u(x,0)&=&0 \\ u(x,M)&=&0 \\\end{align}$

In order to solve this equation, let's consider that the solution to the homogeneous equation will allow us to obtain a system of basis functions that satisfy the given boundary conditions. We start with the Laplace equation: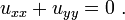 $u_{xx}+u_{yy}=0~.$

Step 1: Separate Variables[edit]

Consider the solution to the Poisson equation as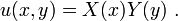 $u(x,y)=X(x)Y(y)~.$ Separating variables as in the solution to the Laplace equation yields:
$X''-\mu X=0$
$Y''+\mu Y=0$

Step 2: Translate Boundary Conditions[edit]

As in the solution to the Laplace equation, translation of the boundary conditions yields: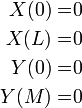
$\begin{alignat}{2} X(0) & = & 0\\ X(L) & = & 0\\ Y(0) & = & 0\\ Y(M) & = & 0\end{alignat}$

Step 3: Solve Both SLPs[edit]

Because all of the boundary conditions are homogeneous, we can solve both SLPs separately.

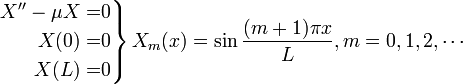
$\left .\begin{alignat}{2} X''-\mu X & = & 0 \\ X(0) & = & 0 \\ X(L) & = & 0\end{alignat}\right \} X_m(x) = \sin \frac{(m+1)\pi x}{L},m=0,1,2,\cdots$

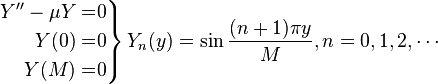
$\left .\begin{alignat}{2} Y''-\mu Y & = & 0 \\ Y(0) & = & 0 \\ Y(M) & = & 0\end{alignat}\right \} Y_n(y) = \sin \frac{(n+1)\pi y}{M},n=0,1,2,\cdots$

Step 4: Solve Non-homogeneous Equation[edit]

Consider the solution to the non-homogeneous equation as follows:

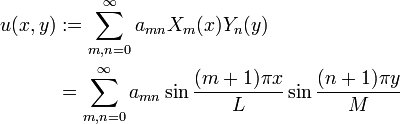
$\begin{align} u(x,y) & := \sum_{m,n=0}^\infty a_{mn}X_m(x)Y_n(y) \\ & = \sum_{m,n=0}^\infty a_{mn}\sin \frac{(m+1)\pi x}{L}\sin \frac{(n+1)\pi y}{M}\end{align}$

We substitute this into the Poisson equation and solve:

$\begin{align}F(x,y)& = u_{xx}+u_{yy} \\& = \sum_{m,n=0}^\infty \left \{ a_{mn}\left \lbrack -\frac{(m+1)^2\pi^2}{L^2} \right \rbrack \sin \frac{(m+1)\pi x}{L} \sin \frac{(n+1)\pi y}{M} \right \} +\left \{ a_{mn}\left \lbrack -\frac{(n+1)^2\pi^2}{M^2} \right \rbrack \sin \frac{(m+1)\pi x}{L} \sin \frac{(n+1)\pi y}{M} \right \} \\& = \sum_{m,n=0}^\infty \underbrace{\left [ -a_{mn} \left ( \frac{(m+1)^2\pi^2}{L^2}+\frac{(n+1)^2\pi^2}{M^2} \right ) \right ]}_{A_{mn}} \sin \frac{(m+1)\pi x}{L} \sin \frac{(n+1)\pi y}{M}\end{align}$ $\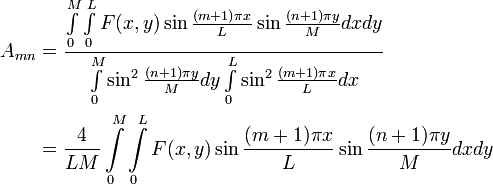begin{align}A_{mn}&=\frac{\int\limits_0^M \int \limits_0^L F(x,y) \sin \frac{(m+1)\pi x}{L} \sin \frac{(n+1)\pi y}{M} dx dy}{\int\limits_0^M \sin^2 \frac{(n+1)\pi y}{M} dy \int\limits_0^L \sin^2 \frac{(m+1)\pi x}{L} dx } \\&=\frac{4}{LM}\int\limits_0^M \int \limits_0^L F(x,y) \sin \frac{(m+1)\pi x}{L} \sin \frac{(n+1)\pi y}{M} dx dy\end{align}$ $a_{mn}=-\frac{4}{LM\left [ \frac{(m+1)^2\pi^2}{L^2} + \frac{(n+1)^2\pi^2}{M^2} \right ]}\int\limits_0^M \int \limits_0^L F(x,y) \sin \frac{(m+1)\pi x}{L} \sin \frac{(n+1)\pi y}{M} dx dy; m,n=0,1,2,\cdots$

Solution to General Case with 4 Non-homogeneous Boundary Conditions[edit]

Let's consider the following example, where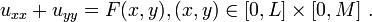 $u_{xx}+u_{yy}=F(x,y), (x,y) \in \lbrack 0,L \rbrack \times \lbrack 0,M \rbrack~.$ and the boundary conditions are as follows:

$\begin{align} u(x,0)&=f_1 \\ u(x,M)&=f_2 \\ u(0,y)&=f_3 \\ u(L,y)&=f_4\end{align}$

The boundary conditions can be Dirichlet, Neumann or Robin type.

Step 1: Decompose Problem[edit]

For the Poisson equation, we must decompose the problem into 2 sub-problems and use superposition to combine the separate solutions into one complete solution.

The first sub-problem is the homogeneous Laplace equation with the non-homogeneous boundary conditions. The individual conditions must retain their type (Dirichlet, Neumann or Robin type) in the sub-problem:

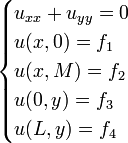
$\begin{cases}u_{xx}+u_{yy}=0 \\u(x,0)=f_1 \\u(x,M)=f_2 \\u(0,y)=f_3 \\u(L,y)=f_4\end{cases}$
The second sub-problem is the non-homogeneous Poisson equation with all homogeneous boundary conditions. The individual conditions must retain their type (Dirichlet, Neumann or Robin type) in the sub-problem:

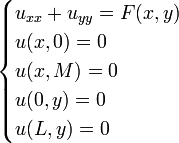
$\begin{cases}u_{xx}+u_{yy}=F(x,y) \\u(x,0)=0 \\u(x,M)=0 \\u(0,y)=0 \\u(L,y)=0\end{cases}$

Step 2: Solve Subproblems[edit]

Depending on how many boundary conditions are non-homogeneous, the Laplace equation problem will have to be subdivided into as many sub-problems. The Poisson sub-problem can be solved just as described above.

Step 3: Combine Solutions[edit]

The complete solution to the Poisson equation is the sum of the solution from the Laplace sub-problem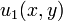 $u_1(x,y)$ and the homogeneous Poisson sub-problem $u_2(x,y)$ :
$u(x,y)=u_1(x,y)+u_2(x,y)$

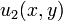来源： http://en.wikiversity.org/wiki/Poisson_Equation

Poisson Equation方程求解--转载