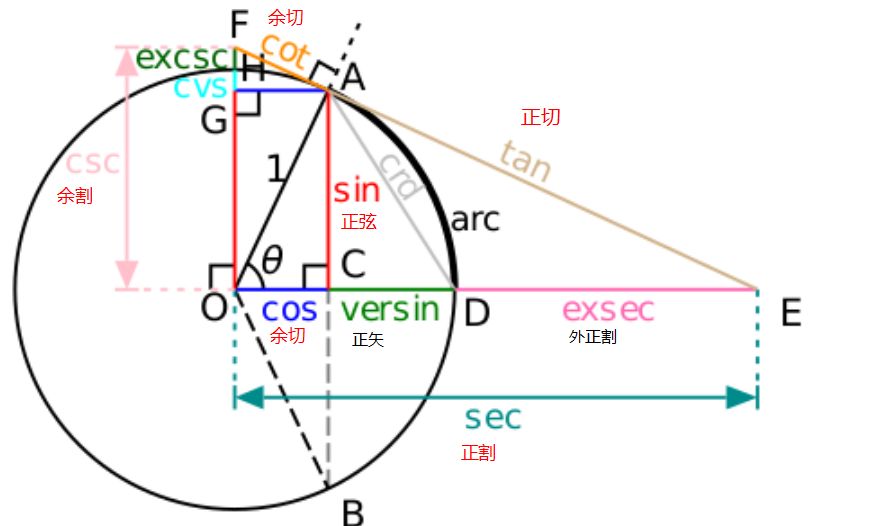
天道有轮回,苍天饶过谁!!!其实数学在我们生活当中或者是工作当中,其实用的地方非常之多,我们今天就来聊一下三角(反三角)函数在javascript中的应用。
先看一下勾股定理
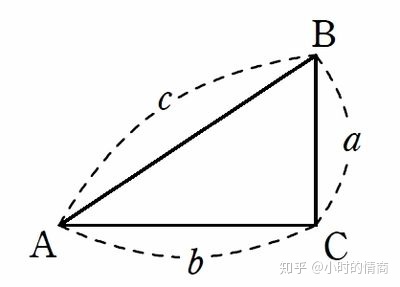
根据勾股定理可以得出
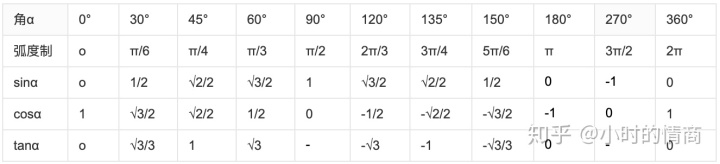
再看几个API
Math.pow() 平方/立方
Math.pow(2,3) // 2的立方
Math.pow(2,2) // 2的平方
Math.sqrt() 开方
Math.sqrt(9) // 3 只能开平方,不能开立方或者是n次方
那
Math.sqrt(Math.pow(3,2)+Math.pow(4,2)) //5
那么勾股定理可以用来做什么呢?勾股定理最容易实现的就是已知两点坐标求距离这样的应用
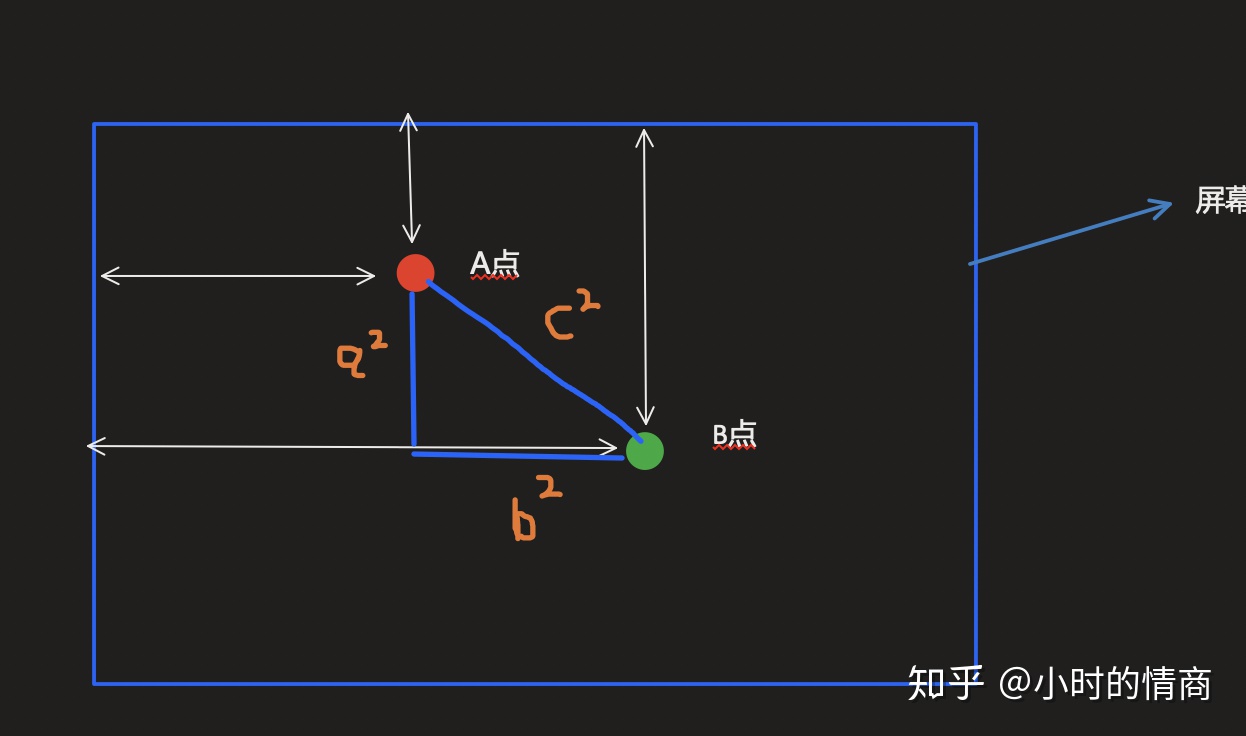
即A点到B点的距离为 c=Math.sqrt(Math.pow(a, 2) + Math.pow(b, 2))
好了,切入正题
三角函数
解决的问题:在直角三角形中,已知一个角度,和一条边,可求出另一条边
三角函数在我们数学当中有很多不同的形式,其中我给大家介绍其中的三种,其实还有很多,我们主要平时用的时候用这三个就够了
在js中分别对应:
Math.sin(弧度)
Math.cos(弧度)
Math.tan(弧度)
注意它们的参数不是角度,而是弧度!!!,因为计算机当中无法表示角度,只能用弧度来表示
那角度与弧度之间是怎么转换的呢?
一圈有多少度呢?一圈就是360度对吧,弧度是什么?弧度是另外一个跟角度有关的单位,就是另外一种写法。为什么会有两种写法?因为角度更多的是在我们生活当中,或者是在咱们数学当中。而弧度一般都是作为计算机当中来使用的,比较专业,计算机都是用弧度来表示的,所以说只要你知道它们之间的一个关系,其实不管是角度和弧度都都是可以换算的。
一弧度概念
首先先来了解一下弧度究竟指的是什么?一弧度到底等于多少?想知道一弧度概念,我们先画一个圆
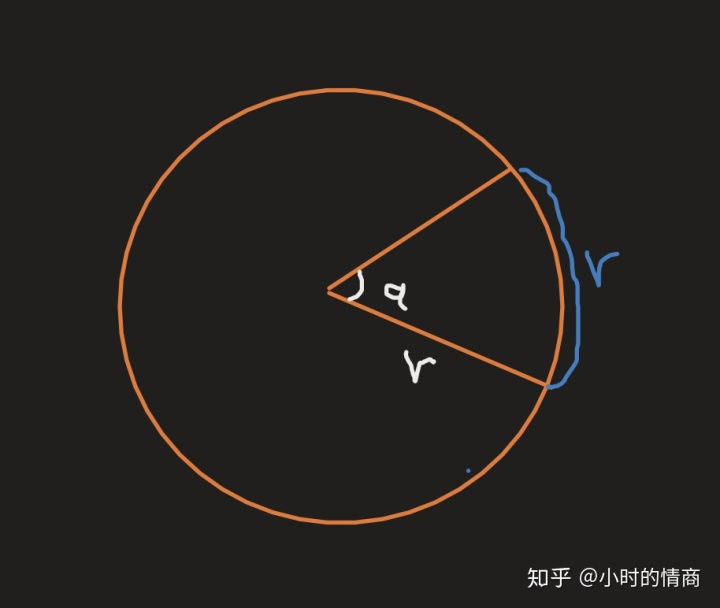
用r表示半径 ,a表示所对应的角度 。那么弧度指角a所对圆的弧曲线这一块,假如说这个曲线它等于半径(r)的话,如果把这个曲线给拉直了,拉直之后,它就等于半径,那么我们就把a这个角度叫做一弧度。所以说一弧度的概念,它其实就是这个角对应的曲线,它的长度如果等于半径(r),就是一弧度。
那整个一个圆,有多少弧度呢?那我们知道r对应的曲线是一弧度,整个有多少个r呢?
我们就需要了解圆的周长该怎么去求。圆的周长就要涉及到另一个概念π。
π=3.1415926......
怎么计算的呢?
有两种计算方式 第一种是圆的周长除以直径等于π,还有一种就是圆的面积除以半径的平方也是π
即
那么
上面说了 一弧度等于半径(r) 那整个圆有多少弧度?
那么整个圆的弧度=
好,既然整个圆它有2π这样一个弧度的话,那一圈所占的角度是多少呢?360度。所以说360度跟2π弧度应该是相等的关系,都是一圈,只不过是两个不同的单位,所以说我们就可以得到这样一个公式
那么角度和弧度都可以换算出来
用弧度来表示1度 javascript写法就是
Math.PI/180
所以在javascript中sin30度就可以这样表示
Math.sin(30*Math.PI/180) //30度角所对应的弧度==>0.5
π在javascript中是一个常量 用Math.PI表示
那么现在我们就来看一个物体做圆周运动的例子
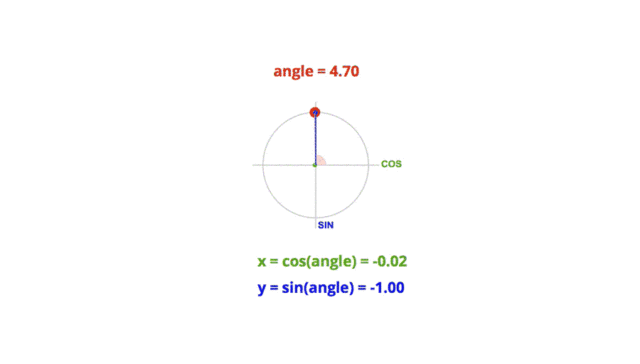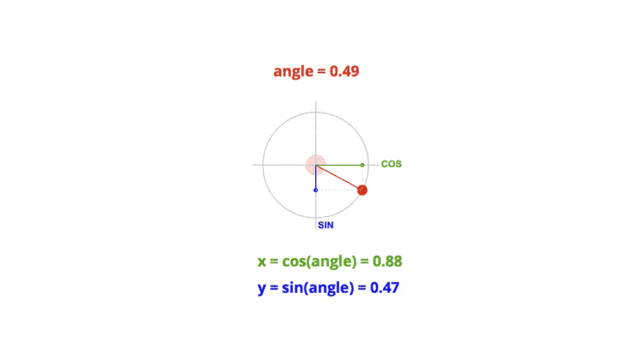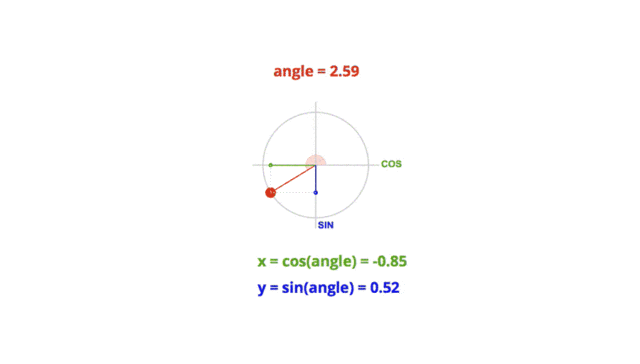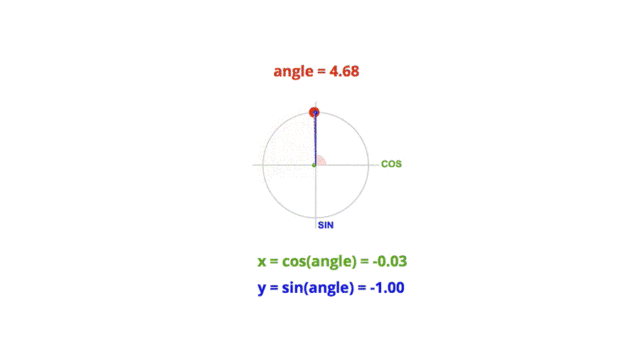
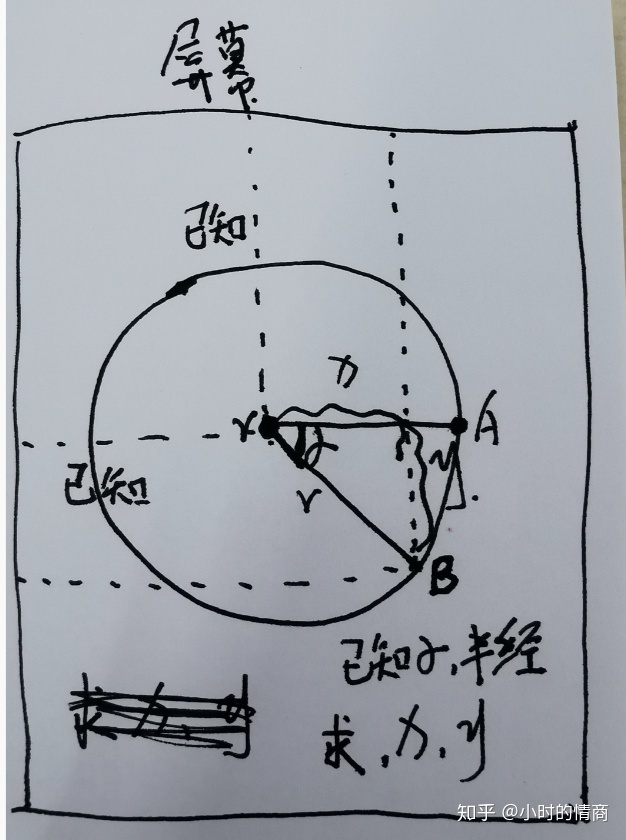
即
Math.sin( 度数*Math.PI/180 ) = y/r圆周运动demogithub.com
Math.cos( 度数*Math.PI/180 ) = x/r
那做一个三维的有立体空间感的圆周运动怎么做呢?
如何能做出来像三维运动这样更复杂的运动,我们需要了解的知识点就更多了,不仅仅只限于三角函数。你需要再配合一些数学、物理等等一些领域的知识,然后才能做出来更丰富的效果。

我们首先先来想第1个问题,上图本身就是一个平面,它没办法去产生三维,那是必须我们要做到一件事情,就是利用这个平面,能够让我们从视觉上感受出来,它是个三维的。好,怎么感受呢?如果说你是学过画画的,你就应该知道三维空间就是近大远小,这样一个概念

比如说这个小一点的圆就相当于是远方。那大一点的圆不就相当于是离你比较近了。如果说我们现在把他们之间加个横线给连起来,这个圆柱是不是就出来了?

好,这个圆柱出来了,是不是就有点立体的感觉了?假如说这是个圆木,然后上面站了一个人
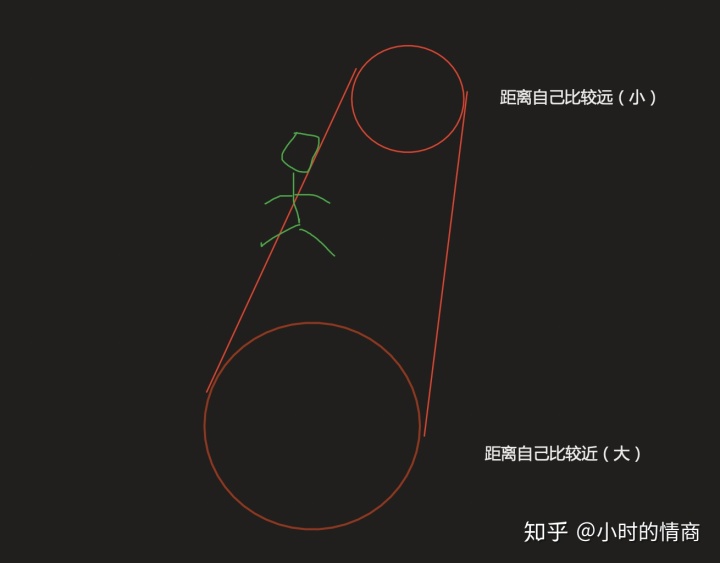
那是不是就可以让这根圆木动起来了呢?
其实发现不需要特别深的一些理念,只是简简单单的近大远小就可以实现3D的效果,利用这样一个概念,我们做圆周运动,立体的三维的圆周运动其实就很容易了,你只需要想象成,它离你近了就大,离远了就小就可以了。
除了近大远小的知识点以外,我们还需要了解一个坐标系。在平面当中我们物体动起来,它是有X坐标和Y坐标就够了,三维的它还有一个Z轴坐标系。
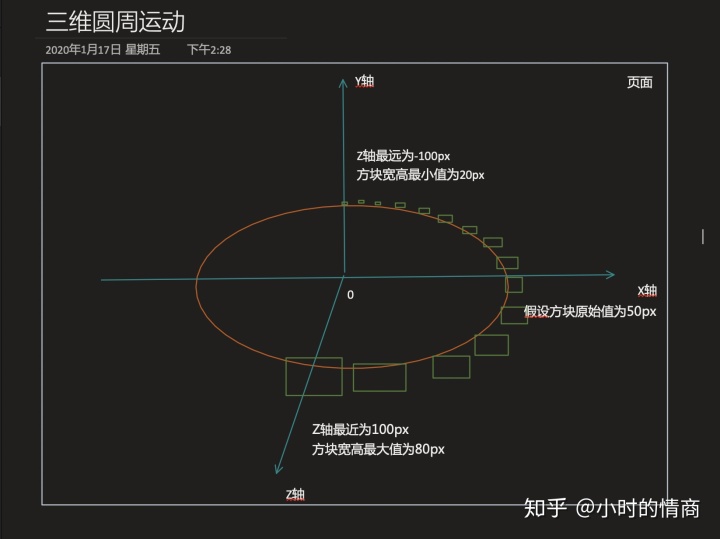
如果方块想让Y轴走的话,大家首先要想一想,top值变没变?其实这个top值并没有变。绕Y轴进行旋转的时候,X轴和Z轴是变的,但是Y轴是不变的。Y轴不变,那说明元素的top值是不变的,对吧。X轴控制什么呢?X轴我们来控制物体的let值,而Z轴控制物体的什么?物体的大小!!!Z轴越大说明物体就越大,Z轴越小说明物体就越小,对吧?这样一个关系。所以说有了这个关系之后就很好做了。
X轴控制物体的let值
Y轴是不变===>元素的top值不变
Z轴越大说明物体就越大,Z轴越小说明物体就越小
再想Z轴最大值和最小值是多少呢?Z轴的绝对值其实就是半径,假如半径为100px,那Z轴最大值为100px,最小值为-100px,其实就是啥呢,Y轴变成Z轴了(多了个正负),Y轴没用了(不变)。Z轴的大小其实是一直在变的
写法为
var x = 700;
var a = Math.sin(度数 * Math.PI / 180) * r;
var b = Math.cos(度数 * Math.PI / 180) * r;
oDiv.style.left = x + b + 'px';
oDiv.style.width = a / 100 * 30 + 50 + 'px'; //100为半径,30为比率,50是方块的原始宽高
oDiv.style.height = a / 100 * 30 + 50 + 'px';
如果说你要想做得更好一点,可以用三维旋转矩阵来做,效果会更炫。
反三角函数
解决的问题:在直角三角形中,已知两条边可求出未知的角度或弧度
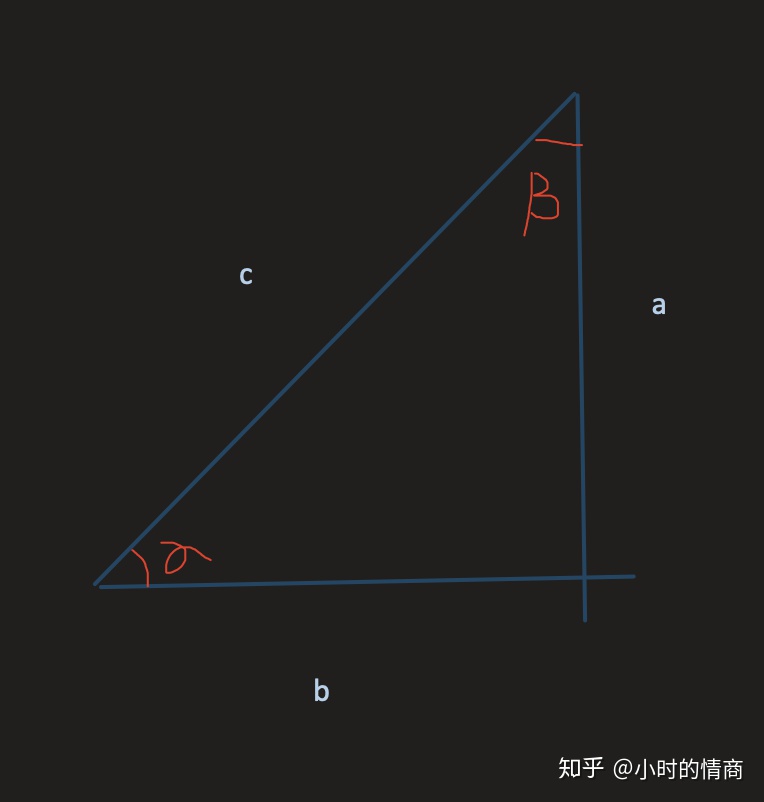
在一个直角三角形中 如果已知a,b,c三边中的两条边 怎么求角
那么就可以用反三角函数来求角度或弧度值。
反三角函数在js中的写法
Math.asin()
Math.acos()
Math.atan()
在反三角函数中求出来的值都是弧度
假如 a=1 c=2 套入公式
Math.asin(1/2) //0.5弧度
怎么转换为角度呢
前面已经讲了
那么
Math.asin(1/2)*180/Math.PI //30度
我们来看一个谷歌的眼睛 案例
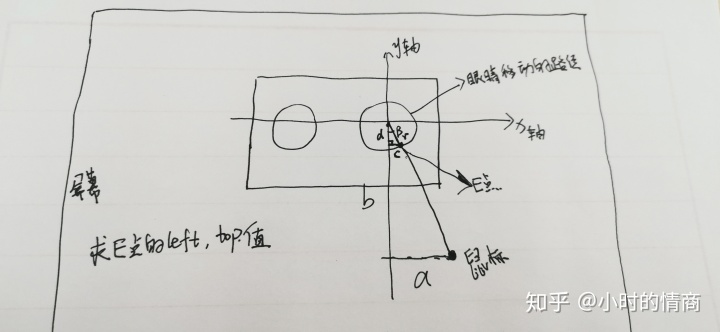
已知a和b可根据反三角函数Math.atan(a/b)求出角
已知斜边r(半径)和角
即而可以求出 E点的left和top值
为什么要划分四个区域呢?
因为直角三角形最大的角度为90度,并且没有负值
谷歌的眼睛demogithub.com圆的碰撞

先了解一下力的分解
合力与分力的概念:如果几个力共同作用在物体上产生的效果与一个力单独作用在物体上产生的效果相同,则把这个力叫做这几个力的合力,而那几个力叫做这一个力的分力
1.力的合成与分解互为逆运算,都符合平行四边形定则:如果用表示两个共点力F1和F2的线段为邻边作平行四边形,那么合力F的大小和方向就可以用F1、F2所夹的角的度数以及大小来表示。
(注:已知分力要求合力,叫做力的合成。已知合力要求分力叫做力的分解。)
2.力的合成与分解的法则:平行四边形法则 [1] 。即力的合成就是由平行四边形的两邻边求对角线的问题。力的分解就是由对角线求两邻边的问题。[1]
力的方向
力的分解与合成,应根据问题的需要灵活处理,即可以按水平、竖直进行分解,也可以按平行和垂直斜面进行分解,至于方向,一是考虑规定一个正方向,与该方向相同的力为正,反方向的力即为负。
圆的碰撞检测
当两个圆的中心点的距离小于等于两个圆的半径之和时 说明碰上了
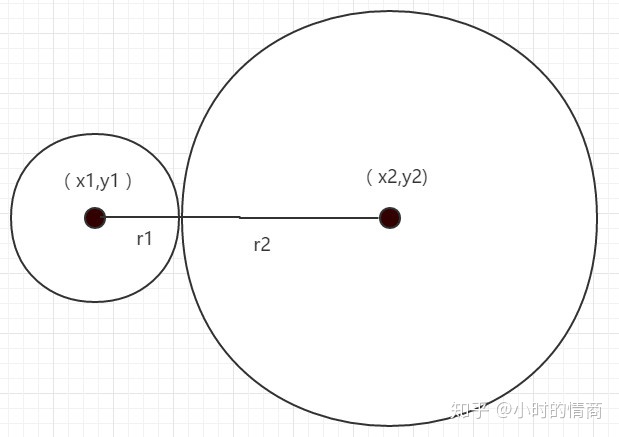
根据勾股定力计算两个中心点的距离
var c = Math.sqrt(Math.pow(a, 2) + Math.pow(b, 2))
如果c<=r+R 就说明两个圆碰上了
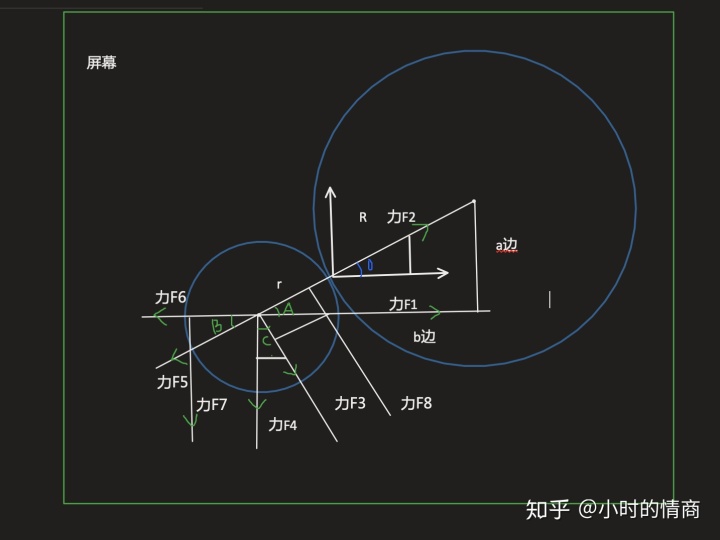
现在开始分解力
如果想用js表示力 那只能用left和top来表示 而lef和top只能用水平方向和垂直方向来表示,所以要把力最终分解成水平和垂直方向,然后再把水平方向上的力相加或垂直方向上的力相加,即可得出left和top值。
假如说小球初始化速度为10
先来计算小圆与大圆碰撞之后小圆受到的力
力F1可分解为力F2和力F3 但是F2和F3都不是水平或垂直的力,所以还得分解。
当小球与大球碰撞之后,向大球方向的力F2会作用到小球上面 即力F5=-力F2
那现在就分析力F5和力F3
力F5可分解为力F6和力F7
力F3可分解为力力F1 和F4
那小球水平方向上的力可表示为 F6+F1
那小球垂直方向上的力可表示为 F4+F7(注意力F4和F7是作用在一起的,但是他们两个受力大小不同)
即我们求出F6+F1和 F4+F7 然后赋值给left 和top即是小圆的运动轨迹
---------------------------------------
根据勾股定理可求出 两圆心之间的距离c
c=Math.sqrt(Math.pow(a, 2) + Math.pow(b, 2))
已知a边和c边根据Math.asin(
假如初始化时速度为10
已知F1和角A根据Math.cos()可求出力F2
力F3怎么求呢
因为 力F3=力F8
所以已知速度和角A可根据Math.sin()=
而力F5=-力F2 角A等于角B
因为小球是从左向右运动的,所以碰撞之后力(速度)会有正负的区分
规定 水平方向的力向右是正 向左是负,垂直方向的力向下是正 向上是负
所以已知角B和F5根据Math.cos(B)=
力F7= Math.sin(B)=
现在我们来求力F1和力F4
因为角A等于角C
已知角C和F3 可求出力F4
又因为角C对应的直角边和F1平行
所以可得出力F1
即小球的
水平方向的速度=(-F6)+(+F1)
垂直方向上的速度=(+F7)+(+F4)
根据上图再来推算大球受到的力(速度)
已知力F2 可以把它分解为向上和向右的力(也就是大圆的速度)
即可得出大圆的left和top值 注意top值为负(因为top值的力是向上的)
圆的碰撞demogithub.com三 , 三角函数图像
如果说你做一些像流体效果的话,你必须得掌握三角函数图像,要不然你做不了流体效果
比如
水波图实现原理 - 掘金juejin.im先看几个概念
单位圆坐标系
一个圆可以在坐标系中用坐标的形式表示出来就是单位圆坐标系
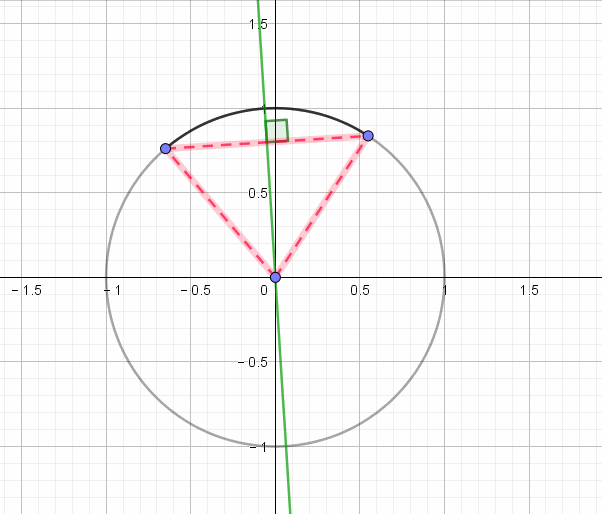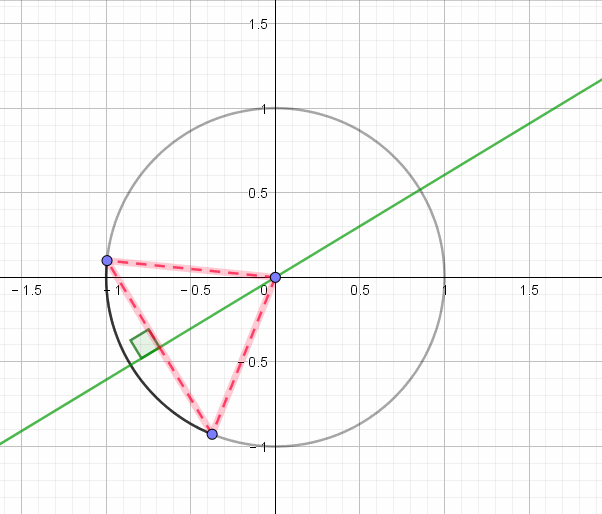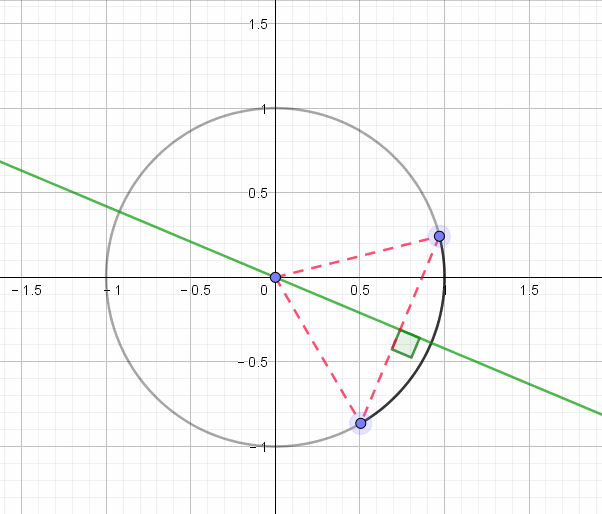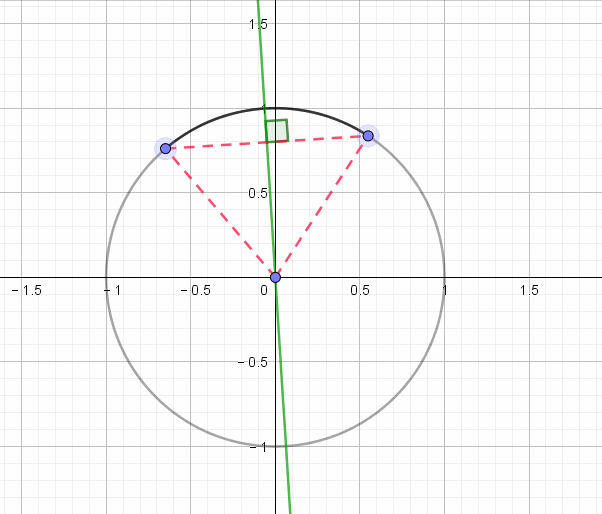
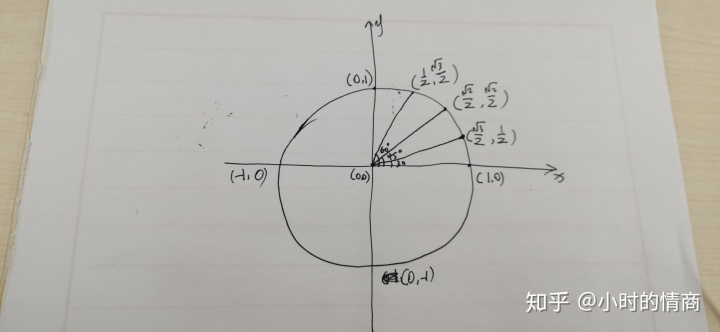
如图所示 x轴其实对应的是cos y轴对应的是sin
那弧度与sin之间有什么关系呢?
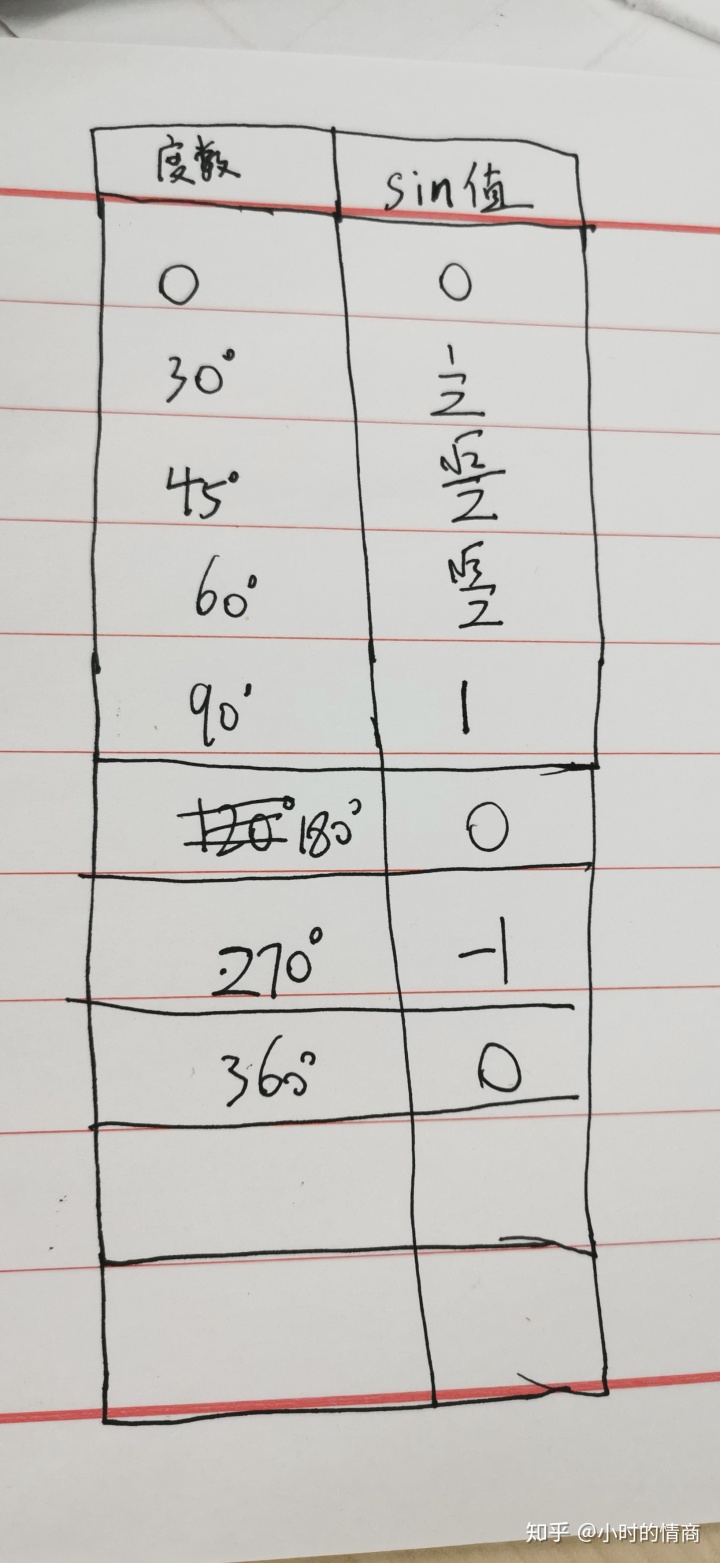
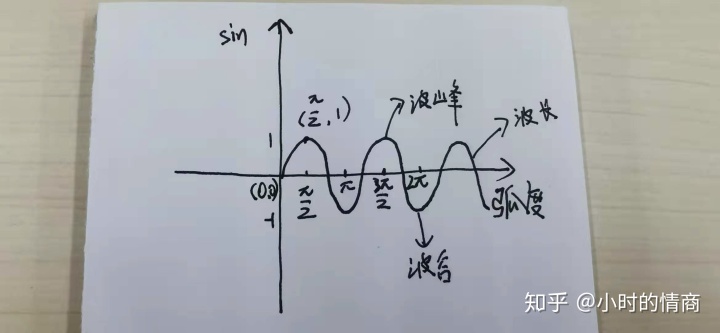
那就可以通过js把这个图像给画出来。正弦函数,余弦函数相应的也可以表示出来
用left表示弧度 top表示角度
wensiyuanseven/public-demogithub.com
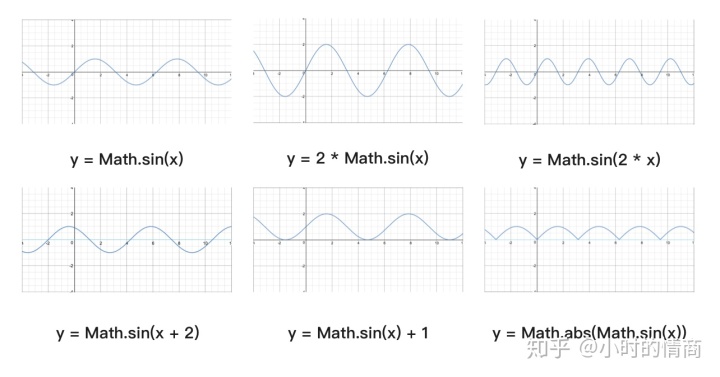
正弦曲线公式:y = A sin(Bx + C) + D
A控制振幅,A值越大,波峰和波谷越大,A值越小,波峰和波谷越小;B值会影响周期,B值越大,那么周期越短,B值越小,周期越长。C值会影响图像左右移动,C值为正数,图像右移,C值为负数,图像左移。D值控制上下移动。
这个公式非常有用,如果下文的代码让你不解,记得回来查看注解。
参考文章
三角函数在前端动画中的应用_JavaScript, Web动画 教程_w3cpluswww.w3cplus.com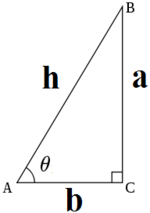
参考
- ^摘自百度百科