机器学习基石笔记

一. 机器学习什么时候用

• 事物本身存在某种潜在规律
• 某些问题难以使用普通编程解决
• 有大量的数据样本可供使用

二. 机器学习的基本流程

1. x 表示输入
2. y 表示输出
3. f: x->y 表示目标函数。要得到，但是不知道的理想函数
4. D:{(x1,y1),(x2,y2),(x3,y3),…} 表示训练集or资料
5. H 表示假说，一个机器学习模型可有多个假设
6. g: x->y 从H中得到一个最好的假设，它对应的函数g与f很像，表示最终的实际函数
7. A 机器学习的核心演算法

机器学习的流程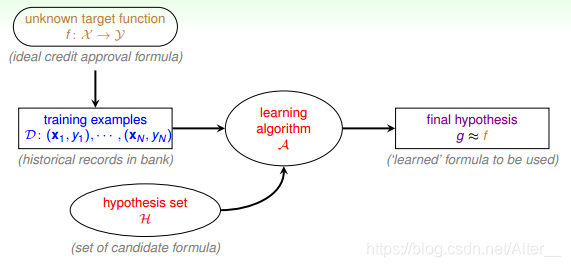

示例：

三. 什么是机器学习

机器学习是什么个人理解：机器学习就是希望机器可以像人一样，通过学习经验得到分析类似问题的方法，从而可以解决问题。
例如：(机器)人做一道数学题没有解题思路(目标函数f未知)，就先看一遍答案(训练集D)，构思几个解题思路(H)，利用答案(D)去套解题思路(通过演算法A)，最后发现正确数学题的解题思路(得到g)，该解题思路不知道是不是与正确的解题思路一模一样，但是他们接近，因为你可以做对一些题目了。

四. 机器学习的可行性

NFL定理

D表示训练集，后面的假设f1~f8的结果都是与训练集输出一样的。然后，下面的输入样本x如101、110…都是在训练集中没有的，也不知道输出多少，可以看到假设的结果都是不一样的。
我们想要在D以外的数据中更接近目标函数似乎是做不到的，只能保证对D有很好的分类结果。机器学习的这种特性被称为没有免费午餐（No Free Lunch）定理。NFL定理表明没有一个学习算法可以在任何领域总是产生最准确的学习器，除非加上一些假设条件。

从统计学中找到可行的方法

1. Hoeffding不等式：
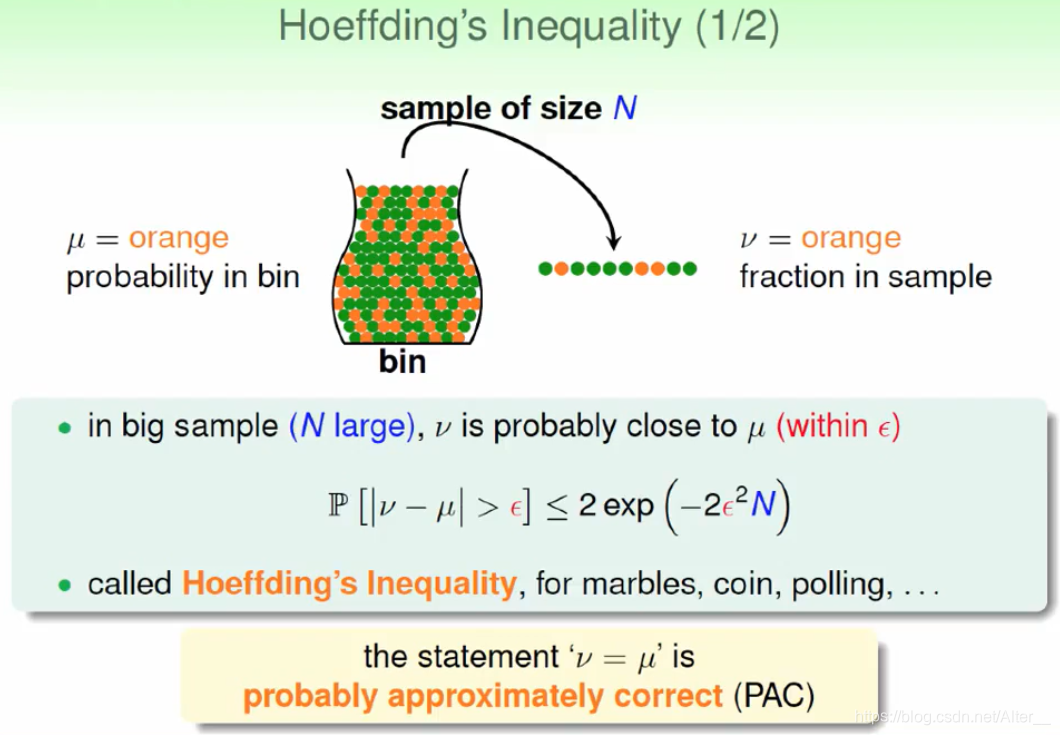
   他告诉我们，我们有很大的几率从抽出来的样本中得到罐子中信息。上面的数学公式满足
   我们得到的结论：如果N足够大，我么可以依靠已知样本推断未知信息。
   

统计学与机器学习产生联系

机器学习中hypothesis与目标函数相等的可能性，类比于罐子中橙色球的概率问题。

1. 一个假设h，E_{in}(h)表示在抽样样本中，h(x)与y_n不相等的概率，我们可以推断E_{out}(h)表示实际所有样本中，h(x)与f(x)不相等的概率是多少。
   
2. 当我们针对一个数据集D，它有多个假设h, 这些假设可能导致不好的资料，即E_{in}与E_{out}相差很远：
   这个是时候根据统计学上给出的定义，不好的资料是因为他们的误差大了，这个概率之和是可以算出来的，由下面的式子我们知道，如果要减小误差大的概率需要去限制h的个数M，这个时候演算法A不管选择什么h成为g都可以得到E_{in}=E_{out}：
   
   对于h个数很多的情况，只要有h个数M是有限的，且N足够大，就能保证E_{in}=E_{out}，证明机器学习是可行的。