作业一中的bonus部分是绕任意过原点轴(单位化为向量n)旋转任意角(α \alphaα),这就要用到经典的罗德里格斯公式了:
R ( n , α ) = cos α I + ( 1 − cos α ) n n T + sin α ( 0 − n z n y n z 0 − n x − n y n x 0 ) R(n,\alpha)=\cos\alpha I +(1-\cos\alpha)nn^T+\sin\alpha\begin{pmatrix} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \end{pmatrix}R(n,α)=cosαI+(1−cosα)nnT+sinα0nz−ny−nz0nxny−nx0
本文主要根据课程的补充材料来做一下这个公式的证明。
补充材料
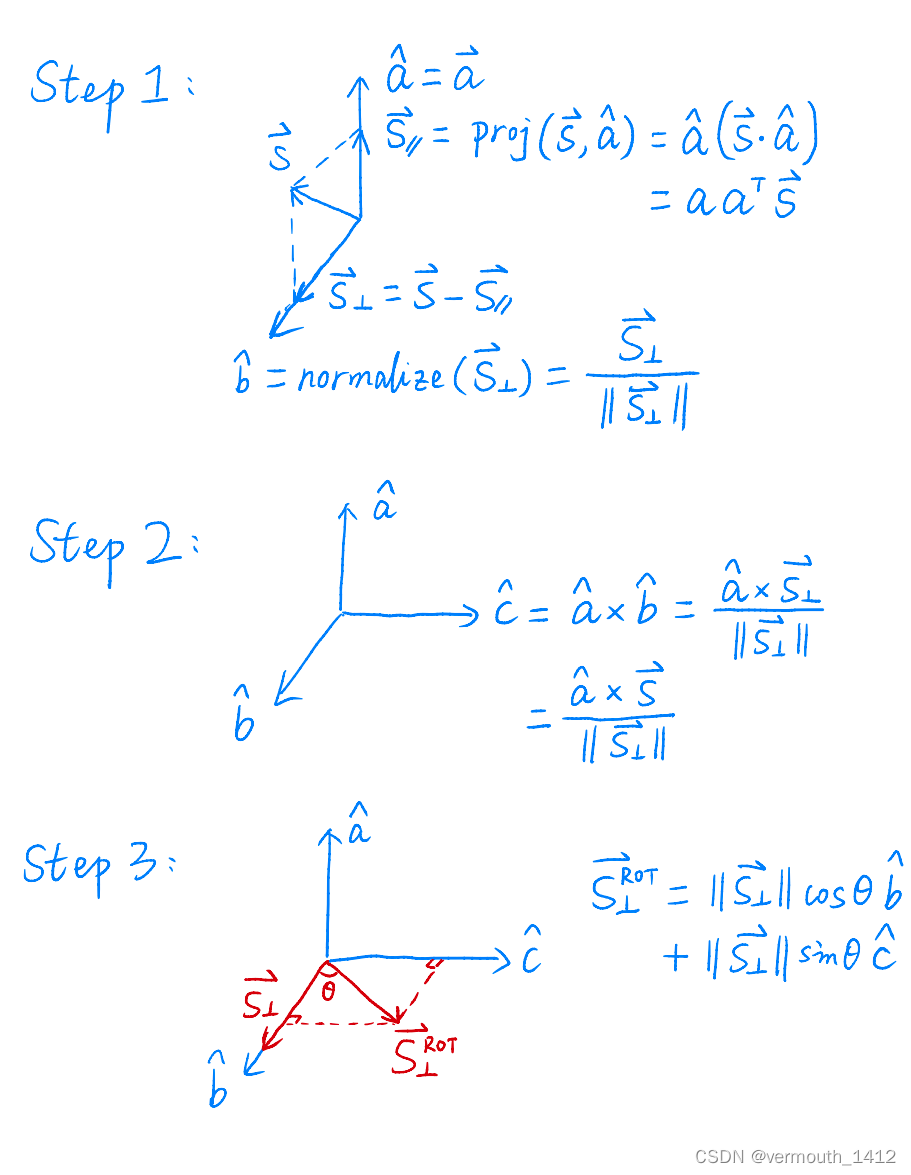
材料说明
上面的补充材料就是老师给的证明。值得一提的是,对于本次要旋转的向量s,其中a、b、c并不是三个坐标轴,而是与本次旋转相关的三个轴:a是本次旋转轴方向的单位向量,b、c是与a构成两两相互垂直的单位向量(需要满足旋转向量s在Oab平面内)。θ \thetaθ是本次的旋转角。
证明方向
通过将旋转轴方向a分离出来,于是我们只需要旋转s中与a垂直的部分,这部分与b平行,而旋转就在Obc平面内进行。旋转后得到垂直旋转部分s v R O T s_v^{ROT}svROT,加上不变的与a平行部分s p s_psp,就可以得到最终旋转后的向量R(a,θ \thetaθ)⋅ \cdot⋅ s。形式化表示如下:
R ( a , θ ) ⋅ s = s p + s v R O T R(a,\theta)\cdot s = s_p + s_v^{ROT}R(a,θ)⋅s=sp+svROT
另外的,根据R ( a , θ ) ⋅ s R(a,\theta)\cdot sR(a,θ)⋅s,我们拥有的参数只有a , θ , s a,\theta,sa,θ,s。
证明步骤
这里前三步根据上面的补充材料,第四步为总结。
Step 1: 分解s及获得b
第一步为在Oab平面内分解s,使其分为与旋转轴平行与垂直的两部分,记平行部分为s p s_psp,垂直部分为s v s_vsv。则分解形式如下:
s p = a ⋅ ( a ⋅ s ) = a ⋅ ( a T ⋅ s ) = a ⋅ a T ⋅ s s_p=a\cdot(a\cdot s) = a\cdot(a^T\cdot s) = a\cdot a^T\cdot ssp=a⋅(a⋅s)=a⋅(aT⋅s)=a⋅aT⋅s
s v = s − s p = s − a ⋅ a T ⋅ s s_v=s-s_p=s-a\cdot a^T\cdot ssv=s−sp=s−a⋅aT⋅s
b = s v ∣ ∣ s v ∣ ∣ b=\frac{s_v}{||s_v||}b=∣∣sv∣∣sv
Step2: 获得c
第二步为通过a、b获得c。该步只需要一次向量叉乘,形式如下:
c = a × b = a × s v ∣ ∣ s v ∣ ∣ = a × ( s − s p ) ∣ ∣ s v ∣ ∣ = a × s ∣ ∣ s v ∣ ∣ c=a\times b=a\times\frac{s_v}{||s_v||}=\frac{a\times (s-s_p)}{||s_v||}=\frac{a\times s}{||s_v||}c=a×b=a×∣∣sv∣∣sv=∣∣sv∣∣a×(s−sp)=∣∣sv∣∣a×s
Step3: 获得s v R O T s_v^{ROT}svROT
第三步为获得s v s_vsv的旋转后形式s v R O T s_v^{ROT}svROT。基于旋转长度不变,我们可以将s v R O T s_v^{ROT}svROT分为平行于b方向与平行于c方向的两部分,二者相加就可以得到s v R O T s_v^{ROT}svROT。形式如下:
s v R O T = ∣ ∣ s v ∣ ∣ ( cos θ b + sin θ c ) s_v^{ROT}=||s_v||(\cos\theta b+\sin\theta c)svROT=∣∣sv∣∣(cosθb+sinθc)
Step4: 整理总结
将b = s v ∣ ∣ s v ∣ ∣ b=\frac{s_v}{||s_v||}b=∣∣sv∣∣sv、c = a × s ∣ ∣ s v ∣ ∣ c=\frac{a\times s}{||s_v||}c=∣∣sv∣∣a×s、s v = s − a ⋅ a T ⋅ s s_v=s-a\cdot a^T\cdot ssv=s−a⋅aT⋅s代入Step3公式可得:
s v R O T = cos θ s v + sin θ ( a × s ) = cos θ s − cos θ a ⋅ a T ⋅ s + sin θ ( a × s ) s_v^{ROT}=\cos\theta s_v+\sin\theta (a\times s) = \cos\theta s - \cos\theta a\cdot a^T\cdot s +\sin\theta (a\times s)svROT=cosθsv+sinθ(a×s)=cosθs−cosθa⋅aT⋅s+sinθ(a×s)
将叉积转化为矩阵乘法得:
s v R O T = cos θ s − cos θ a ⋅ a T ⋅ s + sin θ ( 0 − a z a y a z 0 − a x − a y a x 0 ) ⋅ s s_v^{ROT}=\cos\theta s - \cos\theta a\cdot a^T\cdot s +\sin\theta \begin{pmatrix} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0 \end{pmatrix}\cdot ssvROT=cosθs−cosθa⋅aT⋅s+sinθ0az−ay−az0axay−ax0⋅s
最后,通过相加平行和垂直分量得到旋转后向量:
R ( a , θ ) ⋅ s = s p + s v R O T = a ⋅ a T ⋅ s + s v R O T R(a,\theta)\cdot s = s_p + s_v^{ROT} = a\cdot a^T\cdot s + s_v^{ROT}R(a,θ)⋅s=sp+svROT=a⋅aT⋅s+svROT
R ( a , θ ) ⋅ s = ( cos θ I + ( 1 − cos θ ) a a T + sin θ ( 0 − a z a y a z 0 − a x − a y a x 0 ) ) ⋅ s R(a,\theta)\cdot s = (\cos\theta I +(1-\cos\theta)aa^T+\sin\theta\begin{pmatrix} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0 \end{pmatrix}) \cdot sR(a,θ)⋅s=(cosθI+(1−cosθ)aaT+sinθ0az−ay−az0axay−ax0)⋅s
消去s就可以得到:
R ( a , θ ) = cos θ I + ( 1 − cos θ ) a a T + sin θ ( 0 − a z a y a z 0 − a x − a y a x 0 ) R(a,\theta) = \cos\theta I +(1-\cos\theta)aa^T+\sin\theta\begin{pmatrix} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0 \end{pmatrix}R(a,θ)=cosθI+(1−cosθ)aaT+sinθ0az−ay−az0axay−ax0
证明完毕~