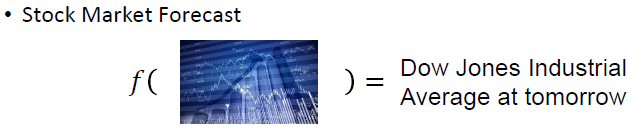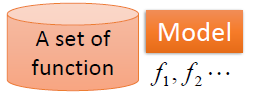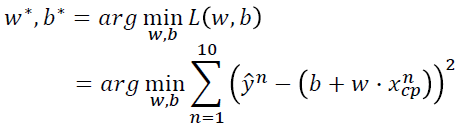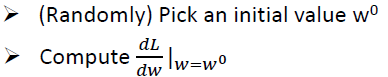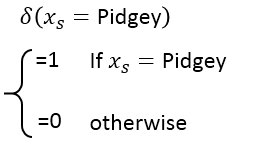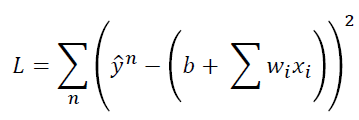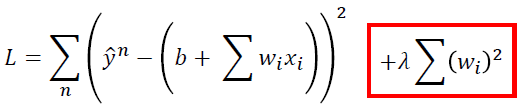//李宏毅视频官网：http://speech.ee.ntu.edu.tw/~tlkagk/courses.html 点击此处返回总目录 //邱锡鹏《神经网络与深度学习》官网：https://nndl.github.io
今天主要讲的是Regression。会通过一个例子讲Regression是怎么用的，顺便引出Machine Learning里面的一些重要概念。 ------------------------------------------------------------------------------------------------------------------------------- 首先，Regression可以做什么？除了作业里面的可以预测PM2.5以外，还有很多非常有用的task： 举例来说，股票预测系统。如果要做股票预测系统的话，要做的事情就是找到一个function，这个function的input可能是过去十年各种股票起伏的资料或者是公司并购的信息。希望这个function在input这些资料之后，output呢，是明天的道琼斯工业平均指数。
另一个例子就是现在很火的无人驾驶，也可以想为Regression的例子。input是无人车看到的各种场景（包括红外线感受到的场景、摄像头拍摄到的场景等），output是方向盘旋转的角度。
另外一个例子就是推荐系统，也可以想象成Regression的问题。输入是使用者A浏览商品B或者A购买B的记录，输出是使用者A买商品B的可能性。这样就可以推荐给用户最有可能购买的商品。
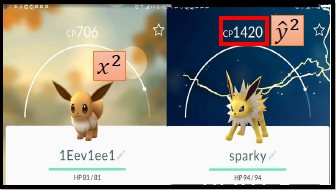
------------------------------------------------------------------------------------------------------------------------------- 上面是Regression的种种应用，今天我们要讲一个更实用的应用：预测宝可梦进化后的CP值。
CP值就是战斗力。当我们抓到一只宝可梦之后，给它吃一些东西，它就会进化，进化之后CP值就会变了。
为什么我们希望预测进化后的CP值呢？因为如果我们能够预测进化后的CP值，我们就可以评估是否选择进化这只宝可梦。如果某一只宝可梦进化后的CP值预测的比较低，那就不去进化它了，就可以省下食物了~~
今天要做的事情就是，找到一个function，input为一只宝可梦的信息，output是这只宝可梦进化后的CP值。 x 表示一只宝可梦。
怎么解决这个问题呢？我们知道（第一堂课讲过）做meahine learning就是3个步骤： 1.找到一个model。model就是function的集合。 2.从model中拿一个function，可以evaluate它的好坏。 3.找一个最好的function。
------------------------------------------------------------------------------------------------------------------------------- 首先从第一步开始，Step1：Model。
一个model，就是一个function set。一个model里面有很多个function f1,f2... 在这个task里面，我们的model应该长什么样呢？ 我们先胡乱写一个： 即，进化后的值y等于某个常数b加上w乘以进化前的cp值。w和b是参数，可以是任意的数值。 在这个model里面，w和b是未知的，可以把任意的数字填进去。填进不同的数值就得到了不同的function。比如，当b = 10.0,w = 9.0时为f1,当b = 9.8, w=9.2时为f2,...如果b和w可以带任何值的话，function可以有无穷个。用式子(1)代表这些function的集合。 在这些function中,显然有一些是不太正确的，比如f3，当进化前cp为正的，进化后变成了负的，这显然是说不通的。这就是后面要靠training data告诉我们这些function里面哪一个才是合理的function。
(1)这样的model是一种linear model。所谓的linear model，简单来说，是指我们可以把一个function写成如下形式： 其中，
------------------------------------------------------------------------------------------------------------------------------- 我们要收集training data才能够找出这个function。这是一个supervised learning，所以要收集的是function的input和output。 因为这是一个Regression的task，所以output是一个数值。 举例来说，当抓了一只杰尼龟，用 杰尼龟进化为卡咪龟，杰尼龟进化后的cp值为979，用
再比如，
我们收集了10只宝可梦，编号从1到10，这些都是真实的data。（有的人会问，怎么只有10只呢？你不知道抓这个很麻烦么~~） 把这10只宝可梦的information画出来的话，如下图，每一个点代表一只宝可梦。(300多这个有三个点) x轴表示这只宝可梦的CP值，即进化前的CP值，这个在抓来的时候就知道了。y轴代表进化后的CP值。
------------------------------------------------------------------------------------------------------------------------------- 有了这些training data以后，我们就可以定义一个funcation的好坏，就可以知道一个function是多好或者多不好。怎么做呢？ 我们要定义另外一个function，叫做Loss function，记做L。这个function很特别，它是function的function。它的输入是一个function；它的输出是一个数值，告诉我们这个function有多不好。 L(f)，表示损失函数以f为参数。而f又是有w、b两个参数决定的。所以input f就相当于input f里面的b和w。所以也可以写作L(w,b)。所以也可以说，L在衡量一组参数的好坏。
那怎么定义Loss function 呢？其实Loss function可以随自己的喜好定义一个自己觉得合理的function。在这里我们用一个比较常见的方法，如下：
如果还有困惑，我们可以把Loss function 画出来。 横纵坐标分别为b和w。整个图是一个model。图中每一个点代表一个function。比如，红色的点，b=-180，w=-2，所以表示y = -180 -2x这个函数。图中的颜色代表该点处Loss function的大小，值越大越偏红，值越小越偏蓝。 可以看到下部的这一堆function是一堆不好的function。上面的一堆function是一堆好的function。最好的function在叉叉这个位置。
------------------------------------------------------------------------------------------------------------------------------- 我们已经定义了Loss function，可以衡量model 里面每一个function的好坏。接下来我们要做的就是从function set里面挑选一个最好的function。挑选最好的function，如果写成公式就是：
找到的f记做f*。 或者可以写成下式： 表示找到w和b，使L(w,b)最小。
如果学过线性代数，理论上应该知道怎么做。假设我们已经忘记了，这里有另一个做法，叫Gradient Descent。
Gredient descent 不是只用来解这一个function的，解这个function是比较容易的，学过线性代数就会了。Gredient Descent比较厉害的地方在于，只要L是可微分的，不管是什么function。Gredient Descent都可以处理这个function，都可以用来帮助我们找到一个比较好的参数。
------------------------------------------------------------------------------------------------------------------------------- 好，那我们来看一下Gredient descent是怎么做的。
先假设一个比较简单的task：Loss function中只有一个参数w。Loss function可以是任何的function，只要是可微分的就行了。现在要解的是 暴力的方法就是穷举所有的w可能的取值，但是这很没有效率。那怎么做呢？这就是Gredient Descent告诉我们的。 做法是这样的：
首先随机选取一个初试的点w0。（其实也不一定要随机选取，有可能有一些其他的方法，可以找到一个比较好的值，日后再说） 然后再w0这个位置，求w对Loss function的微分，这里结果就是切线斜率。如果切线斜率是负的，显然左边的Loss function比较高，右边的Loss function比较低，要找到Loss function比较低的function，应该增加w的值。假如对微分和切线斜率都不是太熟的话，可以想成一个人站在w0点，他先看看往左走一步Loss function减少还是往右走一步Loss function减少，再决定往左走还是往右走。
总之，这个例子中，w应该增加。那增加多少呢？有关Gredient Descent的理论留到下一节再讲，这里只讲操作。
w0往右走一步的step size取决于两件事：一是现在的微分值dL/dw。微分值越大，代表现在在一个越陡的地方，往右移动的距离就越大。二是，取决于一个常数项η，称作learning rate。η是一个事先定好的数值，定的大一点的话，那踏出一步的时候，参数w就更新的幅度比较大，反之更新的幅度比较小。比较大的话，学习效率就比较高，速度就比较快。
这样就由更新到了w1，接下来就重复w1这个地方的微分值，然后再移动。从w1到w2移动距离比从w0到w1小一点，因为微分值变小了。 经过多次iteration以后，会找到一个Local minima的地方。这是因为这个地方微分为0，参数就会卡在这个地方，没法再更新了。
------------------------------------------------------------------------------------------------------------------------------- 刚才讨论的是，只有一个参数的情形。那么有两个参数呢？从一个参数推广到两个参数没有任何不同。
首先随机选取两个初始值w0和b0; 然后计算w=w0,b=b0处，w和b对L的偏微分; 计算完之后，分别更新w和b; 再计算微分，更新 重复以上步骤，就可以得到Loss相对比较小的w和b值了~
要补充说明的是gradient是什么，百度百科解释如下： 梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。
所以梯度是一个向量。在这个例子中，梯度为：
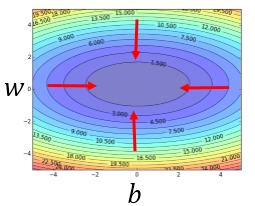
我们可视化一个刚才做的事情： 图中颜色依然代表Loss function的取值，越偏蓝色Loss越小。随机选择初始点，计算dL/db、dL/dw，然后按照梯度方向更新b和w。 梯度方向实际上就是等高线的法线方向。
------------------------------------------------------------------------------------------------------------------------------- Gredient descent 有一个让人担心的地方，就是如果Loss function长成下面这个样子，那就麻烦了。选在不同的初始点，得到的结果不一样，也就是说Gredient descent方法得到的结果是看人品的。 但是在Linear regression里面，不用担心这个问题。因为它的Loss function是convex的，换句话说它是没有局部最小值的。我们把它的图画出来是这样的： Linear regression的Loss function的等高线就是一圈一圈的椭圆形。没有local minmum,随便选一个初始点，根据Gredient descent，最终找出来的都是同一组参数。
------------------------------------------------------------------------------------------------------------------------------- 我们来计算一下对Loss function求偏导数，学过求导的应该都能很容易算出来： ------------------------------------------------------------------------------------------------------------------------------- 其实对于这个问题，Gredient descent并没有想象中那么好解。我们可能认为Gredient descent是一个很trivial的问题，尤其是现在Loss function又是convex的，应该是秒做吧。但是实际上是还是挺费劲的，可以做作业的时候试试。实际上对于这10个点的example，是出了一些狠招才解掉的。
那结果是怎么样的呢？我们的model是蓝色的式子。费劲一番工夫之后，根据training data，找出来的b和w分别为-188.4和2.7。把b和w画在图上，我们得到的function是红色这条直线。 这条直线没有办法完全地匹配宝可梦进化后的CP值。如果想要知道它有多不好的话，可以计算一下error。计算蓝色点和红色点之间的距离，分别记为e1,e2,...,e10。平均的training data 上的error为31.9。 但是这并不是我们真正关心的，因为我们真正关心的是generalization的case。也就是说，假如今天抓到一只宝可梦，如果使用现在的model去预测的话，做出来的估测误差到底有多少。 真正关心的是没有做过的新的data，我们叫testing data，它的误差是多少。所以我们又抓了10只宝可梦，当做testing data。这10跟前面拿来训练的10只不是同样的10只。画在图上如下：
其实这10只新抓的跟刚才的10只的分布还蛮像的，就是图上的10个点。我们发现刚才在训练集上训练出来的这条直线其实也可以大致上预测我们没有见过的宝可梦进化后的CP值。 如果想要量化一下他的error的话，计算一下得到平均误差为35.0，这个值比在training data上的error还要稍微大一点。因为，最好的error是在training data 上找到的，所以在training data上算出来的error本来就应该比testing data上算出来的稍微小一点。
好，那有没有办法做的更好呢？如果想要做得更好，接下来要做的事情就是重新设计model。我们观察一下data会发现，在Original CP特别大和特别小的地方预测的比较不准。可以想想，任天堂在做这个游戏的时候，他背后一定有个function来根据某些属性计算CP值，到底这个function长什么样呢？从结果来看，这个function可能不是一条直线，他可能稍微复杂一点，所以呢，我们需要一个更复杂的model。
------------------------------------------------------------------------------------------------------------------------------- 举例来说，我们可以引入二次式。我们引入 有了这个式子，我们可以用更刚才一样的方法去定义一个function的好坏，然后用Gredient descent方法找到一个在function set 里面最好的function。 根据training set 找到的最好的function如左边所示，画在图上为长右边这样。我们会发现，现在我们这个新的model，这个新的函数在trainding data上预测的更准一些。在training data上得到的average error为15.4。 但我们真正关心的是在testing data。用同样的函数，在testing data上，计算error为18.4。在没有考虑二次项的时候，error为35。好了很多。
------------------------------------------------------------------------------------------------------------------------------- 那有没有可能做得更好呢？我们考虑一个更复杂的model,引入三次项。现在的model如蓝色部分所示。
用一模一样的方法，根据training data 找到的model 里面的最好的function如左边所示。w3的值很小，可能没有什么影响。画出来的图像感觉跟二次的差别不大，计算一下average error为15.3，比二次的15.4小一点。 如果看testing data，error为18.1,比刚才的稍微好一点点。
------------------------------------------------------------------------------------------------------------------------------- 那有没有可能是更复杂的model呢？或许在宝可梦程序的背后用到了更复杂的function，或许他不止考虑了三次。或许他考虑了4次也说不定。 用同样的方法把参数找出来，得到的function长这样子。发现在training data上可以做得更好，为14.9。但是我们真正关心的是没有见过的宝可梦，我们能多么精确地预测它的CP值。在testing data上的结果为28.8。前一个已经是18.1了，这个的结果居然更糟了。 我们发现我们使用了一个更复杂的model,在testing data上给了比较好的结果，但是在testing data上结果更糟了。
------------------------------------------------------------------------------------------------------------------------------- 我们换一个更复杂的model，有没有可能是五次式。 计算的结果长这样。但这不是一个合理的结果，因为在500附近得到的CP值是负的。 但是在training data上计算出来的结果为12.8，比用四次的式子还要好一些。 在testing data上，发现整个结果烂掉了。在500多这个点上，预测的非常不准。平均error非常大。
------------------------------------------------------------------------------------------------------------------------------- 到目前为止，我们试了5个不同的model。把这5个model在training data上的error画出来如下： 我们发现error越来越小。也就是，model越复杂，在training data上的error越小。 为什么会这样呢？这件事情也非常容易解释。
假设黄色圈圈为model 3所形成的function space ，model 4形成的function space 为绿色圈圈。绿色的圈圈包含黄色的圈圈，因为只要将w4设为0,4式就变成了3式。5式形成的圈圈又包含4式的圈圈。 所以呢，一个越复杂的model，他包含了越多的function，那么理论上呢，就可以找到一个function让error越低。前提就是如果能够真的找到每个model中最好的函数。
------------------------------------------------------------------------------------------------------------------------------- 但是在testing data上面，结果就不一样了。在training data上可以说，model越复杂，error越低。但是在testing data上，到第3个model，error是下降的。但是之后就暴增了。把图试着画在左边这边，蓝色是training data上对不同model的error，橙色是testing data上对不同model的error。
我们发现5次model在testing data上的error是爆炸的，已经画不出来了。 所以我们今天得到一个观察：虽然越复杂的model可以在training data上给我们越好的结果，但这件事情也没什么，因为越复杂的model并不一定在training data上给我们约好的结果。这件事情就叫做overfitting。 复杂的model在training data有越好的结果，但是在training data上不一定有好的结果，这个事情叫做overfitting。比如，当我们用第4、第5个model的时候，就发生了overfitting。 为什么会有overfitting呢？这个日后再解释。其实可以想到很多很直观的例子，比如考驾照，在驾校学习的时候会学到很多很奇怪的技能，比如当后视镜看到一块小石头，就往左打半圈方向盘。当真正上路的时候就做不好了。 所以呢，overfitting是很有可能会发生的。所以model不是越复杂越好，我们必须选一个刚刚好，合适的model。比如这里选model 3，可以给我们一个比较好的结果。
------------------------------------------------------------------------------------------------------------------------------- 这样就结束了么？其实还没有。刚才只收集了10只宝可梦，太少了。当我们收集到60只的时候，会发现刚才都是百忙一场。把这60只宝可梦画到图上： 我们发现并不是一次、二次、三次...的关系。这中间有另外的力量，不只是CP值影响着进化后的数值。到底是什么呢？直觉告诉我们是宝可梦的物种。 我们把不同的物种用不同的颜色来表示，如上图所示。蓝色是波波，绿色是绿毛虫，黄色是独角虫，红色是伊布。 所以只考虑进化前的CP值显然是不对的，因为进化后的CP值收到物种的影响还是很大的。所以刚才设计的model都不好。 刚才在model里面找最好的function就好像是大海捞针，但是针根本就不在海里。前面的model统统都不好。
------------------------------------------------------------------------------------------------------------------------------- 回到第一步，我们重新设计function set。设计的model如下： 当物种不同的时候，我们就带入不同的linear function。然后得到y作为输出。 这里有一个问题，把if放到整个function里面，这样还是一个linear的model么？搞的定么？可以用微分来做么？可以用Gredient descent 来算微分么？ 其实是可以的。这个式子可以改写成一个linear function，如下： 其中， 而这个function就是linear function，怎么说呢？前面的b1,w1,b2,w2,b3,w3,b4,w4就相当于下面的wi，而蓝色框框中的部分就相当于xi，就是特征。
------------------------------------------------------------------------------------------------------------------------------- 对于上面的model，我们做出来是什么样的呢？ 上方的图为在training data 上的结果。不同物种的宝可梦的先是不一样的。当分物种考虑的时候，model在training data上面可以得到更低的error，这几条线把training data fit地更好，解释地更好。 下方的图是在testing data上的结果。发现也fit得很好。average error 是14.3。
但是在观察图的时候，感觉应该还有一些东西是没有做好的。我们仔细想想，伊布（红色）这边感觉就这样了，我认为伊布有很不一样的CP值是因为它能进化成不同种类的精灵，如果没有考虑到这个feature的话，基本就这样了。 但是其他的线，觉得还有没有fit得很好的地方，有一些值还是略高或略低于直线，这个地方不好还是有办法解释的。当然还有一种可能就是，这些略高或略低于直线的difference其实来自于random的数值。每次程序产生一个CP值的时候，会加一个random的参数。也有可能不是random的参数，还有其他的东西会影响进化后的CP值。
------------------------------------------------------------------------------------------------------------------------------- 还可能有什么样的参数呢？会不会跟weight有关系，会不会跟height有关系，会不会跟HP有关系？ 我们也没有domin knowledge，怎么办呢？ 有一招，就是把所有想到的统统塞进来。我们来弄一个最复杂的function，看看会怎么样。model如下： 一共有18个参数，与作业里面几百个参数比起来也不是特别复杂。这个式子可以根据前面的方法写成线性的，就不解释了。 这么复杂的model，在training data上的error为1.9。在testing data 上面的结果为102.3,过拟合了！
------------------------------------------------------------------------------------------------------------------------------- 怎么办呢？如果我们是大木博士，我们就可以删掉一些觉得没有用的input，就可以得到一个比较简答的model，就可以避免overfitting了。但是我们不是大木博士，我们用别的方式来解决这个问题，这招叫做Regularization(正则化)。 Regularization要做的事情就是，我们重新定义了一个function是好还是坏，即重新定义了Loss function。我们在原来的Loss function的基础上加上了一些knowledge，让我们可以得到比较好的参数。 具体做法就是，假如我们的model如下： 我们原来的Loss function 只考虑了error这件事，如下： 而正则化就是，在原来的Loss function 的基础上，加上了额外的一项，变成以下的形式： 其中，λ为一个常数，这个等一下我们要手调一下是多少。
对于Loss function的前半部分，我们已经知道，表示error越小越好。而加上了红色的部分，就表示wi越小越好。 我们为什么要期待一个参数的值接近0的function呢？
首先，参数值接近0的function是比较平滑的function。所谓比较平滑的意思就是，当输入有变化的时候，output对输入是比较不敏感的。为什么参数小，就比较不敏感，就比较平滑呢？ 可以想想看，假设
其次，我们为什么要期待一个比较平滑的function呢？可以这样想，如果我们有一个比较平滑的function的话，平滑的function对输入比较不敏感。那如果我们的输入被一个噪声干扰的话，一个比较平滑的function会受到较少的影响而给我们一个比较好的结果。
------------------------------------------------------------------------------------------------------------------------------- 那接下来看一下，加入了正则项之后，会给我们带来什么影响。
这是实验的结果，λ从0，到1，一直到10万。λ越大代表考虑平滑的那一项的影响越大。λ越大，说明找到的function越平滑。
我们看一下training data上的error，发现越平滑，error越大。这件事是非常合理的，因为当λ越大时，我们就偏向于考虑wi本身的值，减少考虑error。所以当λ越大，考虑error越少。所以在training data 上得到的error越大。 但是有趣的是，虽然training data上得到的error越大，但是在testing data上得到的error可能会比较小。比如当λ=100时，error为11.1。 这个结果也是合理的，因为我们喜欢比较平滑的function，比较平滑的function对噪声比较不敏感，所以当增加λ时，performance越来越好。但是我们又不喜欢太平滑的function，因为最平滑的function就是一条水平线，如果是水平线，那什么也干不成了。所以如果function太平滑的话，反而会得到很糟糕的结果。所以，现在的问题是看我们的model多平滑，这件事就必须通过调λ来解决。比如这里λ为100时，得到比较好的model。
还有一个问题就是，正则项里面是没有把b这一项加进去。这是因为b对于平滑没有什么影响，b负责function的上下移动，对Δy没有影响。 总之，我们今天搞了半天，最后可以做到testing data 上的error是11.1。
------------------------------------------------------------------------------------------------------------------------------- 最后，来做一个总结。 1. 宝可梦的研究进展。 2. Gradient descent的原理和技巧，后面讲。 3. 问题：今天我们得到的testing data 上的error为11.1。如果把这个系统开源到线上的话，请问得到的error是大于11.1还是小于11.1还是等于11.1？ 答，会大于11.1，这个需要用validation的知识来解释，以后讲解。
|
表示这只宝可梦进化前的CP值，图中为14。 //我们用下标表示一个完整的东西里面的某一部分。csdn没法写下标，所以截图了。
表示物种。图中这只宝可梦是妙蛙种子。
表示生命值。图中这只宝可梦生命值为10。
表示重量。
表示高度。
(1)
代表x的不同的属性，叫做feature。
来表示它。 //我们上标来表示一个完整的个体的编号。
来表示。 //用y来表示function的output，上标代表完整的个体，^表示这个一 个正确的值，是我们实际观察到的function该有的output。
的含义为：如果使用这一组b和w当做我们的function，来预测xn，预测进化后的CP值为
。
的含义为：真正的进化后的CP值减预测的CP值，再取平方，也就是估测误差。
：最后将10只宝可梦的估测误差加起来，得到Loss function。
表示：要找到一个f，使得L(f)最小。
这个式子，即找到一个w，使L(w)最小。怎么做呢？
这一项。我们重新设计了一个model，如下标蓝的式子。
是我们的model，当input的xi有一个变化 Δxi 时，y的变化是
