- 实训目的
数据结构实训是计算机科学与技术专业集中实践环节之一。数据结构是本专业一门重要的专业基础课程,是一门关键性核心课程。该课程较系统地介绍了软件设计中常用的数据结构以及相应的存储结构和实现算法,介绍了常用的多种查找和排序技术。该课程将为整个专业的学习以及软件设计水平的提高打下良好的基础。
数据结构是一门实践性较强的课程,为了学好这门课程,必须在掌握理论知识的同时,加强上机实践,设置数据结构实训环节十分重要。
- 实训项目要求
本次实训我选择的题目是二叉树的遍历与应用算法设计与实现
二叉树是树形结构的一个重要类型,许多实际问题抽象出来的数据结构往往是二叉树类型,应用极为广泛。本次课程设计使用二叉链表来建立二叉树的存储结构,利用栈和队列来实现二叉树的中序非递归遍历和层序遍历,并利用递归来实现二叉树的先序、中序、后序遍历。本次设计还实现了计算二叉树中的叶子结点个数、求二叉树的深度、将二叉树中所有结点的左右孩子互换以及判断二叉树是否为完全二叉树等二叉树的应用算法。
本次设计使用的编程语言是C语言,使用的Microsoft Visual Studio2010编译实现。
- 实训项目实现
- 功能分析:

图1 系统模块结构图
(1)建立二叉树:利用二叉链表建立二叉树的存储结构。利用链式存储结构来存储一颗二叉树,即用链来指示元素的逻辑关系,二叉树中的每个结点用链表中的一个链结点来存储。
(2)实现二叉树的层序遍历:利用队列实现二叉树的层序遍历。队列是一种先进先出的存储结构,仅允许在表的前端进行删除操作而在表的后端进行插入操作,利用队列实现二叉树的层序遍历更加简洁和方便。
(3)实现二叉树递归遍历:利用递归的算法来实现二叉树的先序、中序和后序遍历。
(4)实现二叉树的中序非递归遍历:利用栈实现二叉树的中序非递归遍历。栈是一种后进先出的存储结构,仅限定在栈顶进行插入和删除操作,可以用栈来实现二叉树的中序非递归遍历。
(5)实现二叉树的应用:二叉树在一些搜索引擎和路由器中应用广泛,这些应用都要用到二叉树的最基本的应用算法:计算二叉树的叶子结点个数、求二叉树的深度、将二叉树中所有结点的左右孩子互换以及判断二叉树是否为完全二叉树。
(6)菜单功能:对二叉树的各种遍历和应用进行选择。
(7)显示功能:将二叉树的遍历和应用结果显示出来。
(8)退出功能:退出整个程序,结束运行。
2、数据结构分析
(1)顺序表是一种静态存储结构,需要预先知道数据大小来申请连续的存储空间,而且进行扩充时需要进行数据的搬迁。相对于顺序表,链表结构可以充分利用计算机的内存空间,实现灵活的内存动态管理且进行数据扩充是不需要数据的搬迁。在实际应用中,虽然顺序表的存取速度更高效,但是在一些搜素引擎中的大部分数据都是需要经常进行更新的,因此对于开发人员来说使用链表的删除和插入操作更有利于对引擎中的数据进行更新,动态分配存储空间,避免进行数据的搬迁。
通过上述分析,我选择二叉链表存储结构,存储结构如下:
typedef int Status;
typedef char TElemType; //二叉树结点的值的类型
typedef struct BiTNode {
TElemType data;//二叉树的结点值
struct BiTNode *lchild, *rchild; //左右孩子指针
}BiTNode, *BiTree; //定义二叉树的存储类型
(2)在进行二叉树的层序遍历时,利用了队列的存储结构。
(3)在二叉树的中序非递归遍历中利用了栈的顺序存储结构。
(4)在二叉树的遍历与应用算法设计与实现中,所有的递归遍历、非递归遍历以及二叉树的应用算法都使用的是同一颗二叉树,即整个程序中只创建了一次二叉树的存储结构,为了方便用户对二叉树的各种算法进行选择,加入了菜单功能,主要算法如下:
printf("请输入数字1-9或者0结束程序:\n");
scanf("%d",&n);
switch(n){
case 1:
……
case 0: exit(0);
break;
}
(5)显示功能,将程序的运行结果输出。
//输出遍历的结点的存储数据值
void PrintElement(TElemType e) {
printf("%c", e);
}
3、关键算法
二叉树的遍历:首先利用二叉链表先序建立二叉树的存储结构,输入一颗二叉树,利用菜单功能依次选择调用PreOrder函数、InOrder函数、PostOrder函数实现二叉树的先序、中序、后序递归遍历,调用LevelOrderTraversal函数利用队列实现二叉树的层序遍历,调用InOrderTraverse函数利用栈实现二叉树的中序非递归遍历。
二叉树的应用算法:构造函数实现二叉树的各种应用算法,再通过调用函数的方式计算一颗二叉树的叶子结点的个数、求二叉树的深度、将二叉树的左右孩子互换、判断二叉树是否为完全二叉树。
(1)利用二叉链表先序建立二叉树的存储结构。算法流程图如图2所示。
(2)二叉树的先序、中序、后序递归遍历。算法流程图如下图3所示。
(3)二叉树的层序遍历。算法流程图如下图4所示。
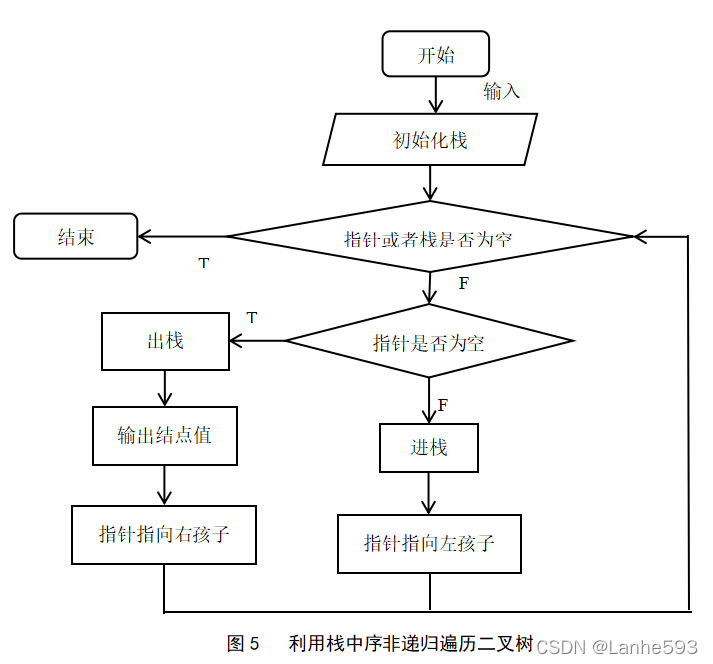
(4)二叉树的中序非递归遍历。算法流程如图5所示。
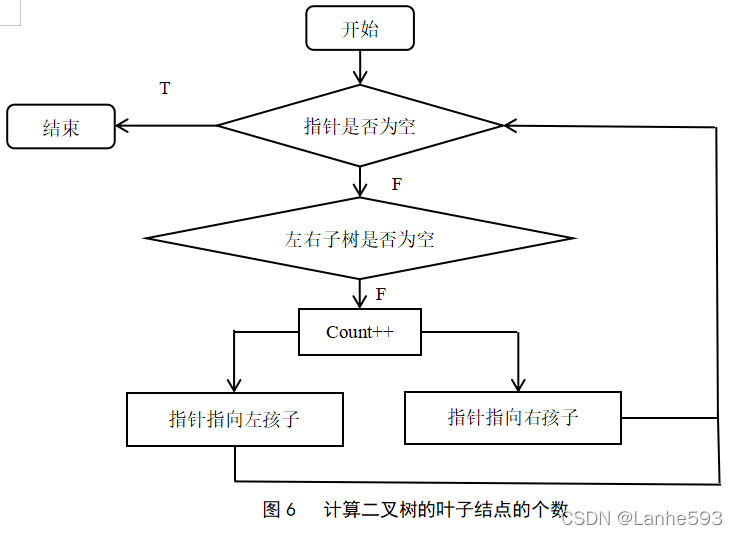
(5)二叉树的应用算法—计算叶子结点的个数。算法流程图如图6所示。
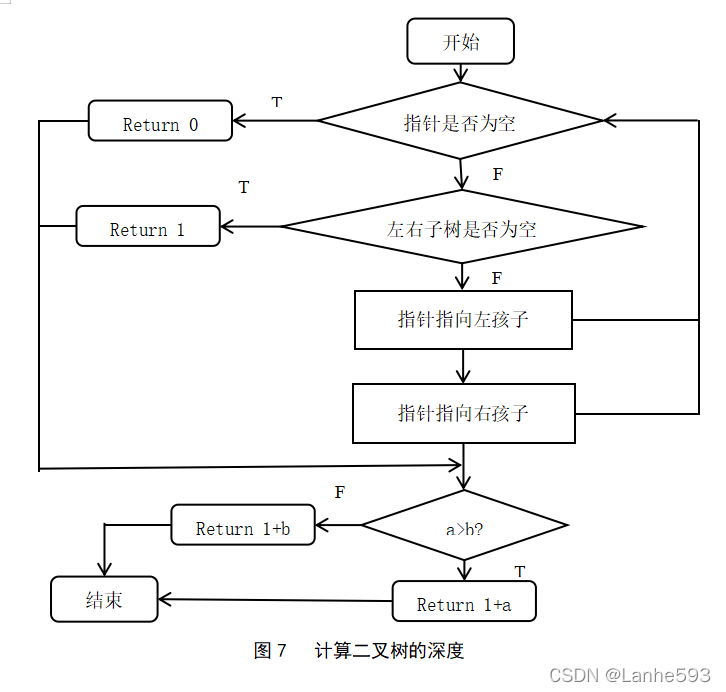
(6)二叉树的应用算法—求二叉树的深度。算法流程如图7所示。
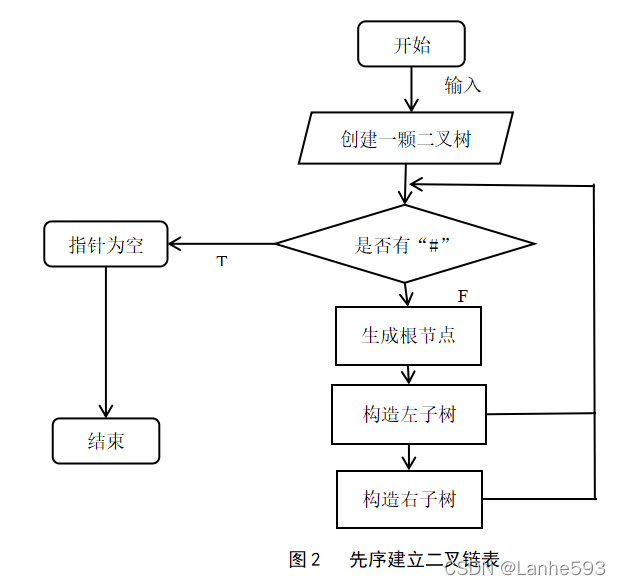
算法描述:
输入一颗二叉树,如果有#则二叉树的结点为空,如果没有#则建立根节点,再依次递归调用当前函数构造左子树和右子树。
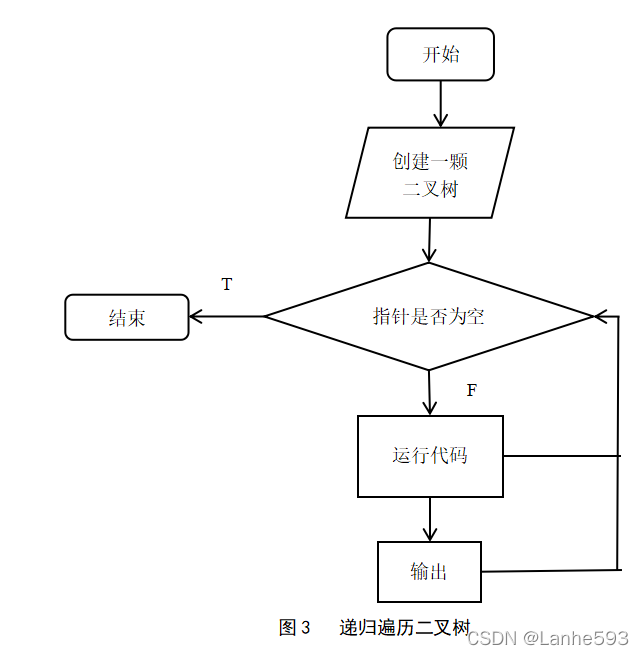
算法描述:
利用队列层序遍历二叉树,首先初始化队列让根节点进队,判断队列是否为空,若不为空则让根节点出队并输出根结点值,依次让左右孩子进队再次进入循环并依次输出结点值。
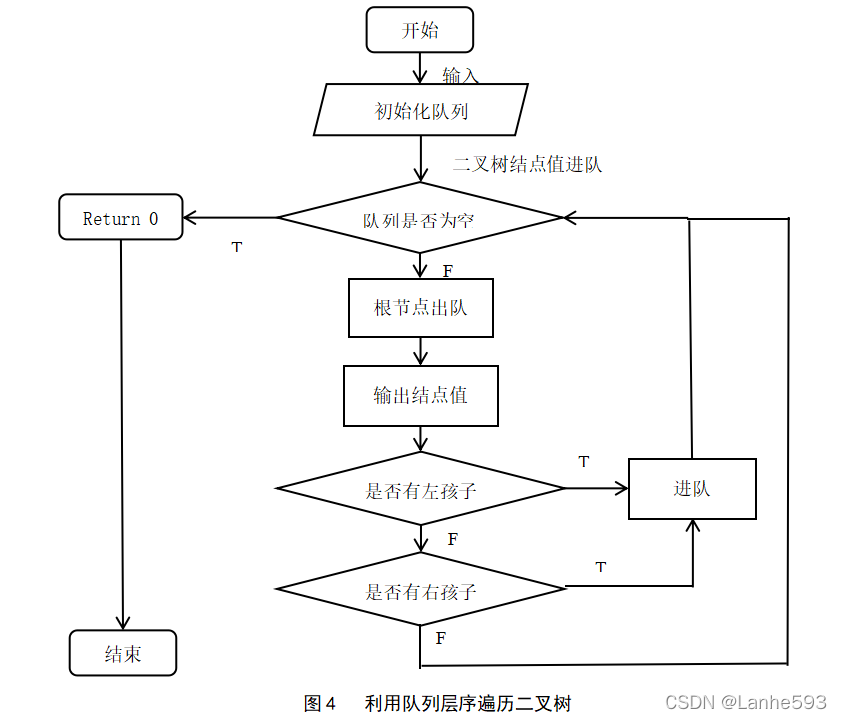
算法描述:
初始化栈,构建一个新的指针P,栈不为空,判断指针不为空则进栈,指针指向左孩子,所有的左孩子进栈。如果指针为空则栈内所有元素出站栈,指针再指向根节点的右孩子,重复上述过程,中序非递归遍历二叉树。
算法描述:
判断指针是否为空,若为空则程序结束,若不为空,如果左右孩子都不为空,执行count++,指针指向左孩子递归调用本函数,指针指向右孩子递归调用本函数。返回count的值。
算法描述:
定义int类型a、b两个元素,如果指针为空则返回0,如果左右孩子指针都为空则返回1,指针指向左孩子递归调用本函数,指针指向右孩子递归调用本函数。如果a>b输出1+a,如果a<b输出1+b,结束。
4、运行测试
- 运行程序,先序输入一颗二叉树:ABC####。注意在先序输入二叉树时一定要把左右孩子为空的情况考虑到,用“#”来代表空。
出现的问题1:若直接输入ABC,则程序运行过程中发生错误导致程序中断。

解决方法:输入ABC####。
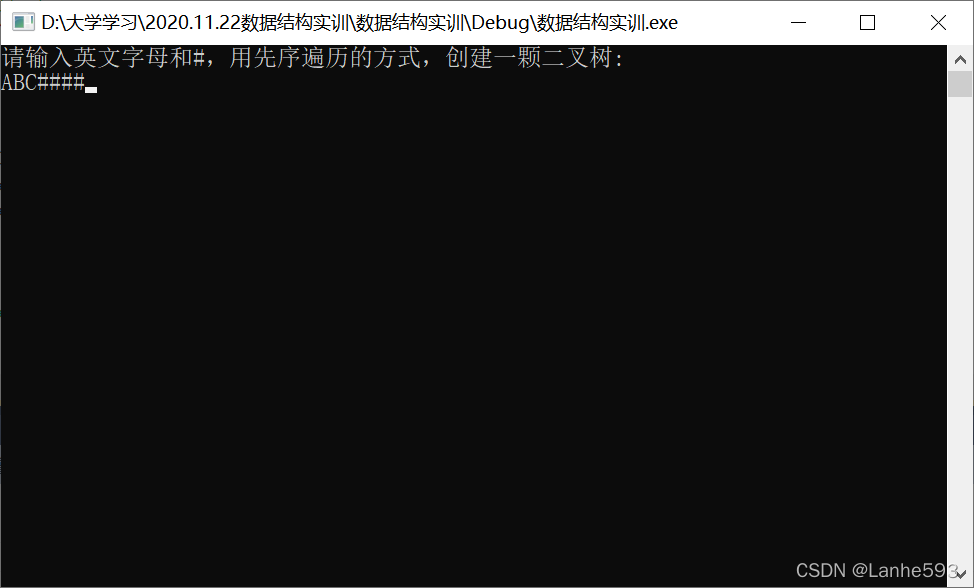
出现的问题2:字符#和字母ABC不能分开写,否则程序中断,将会一直处于输入状态,无法正常运行。
解决方法:连续且正确的输入ABC####

- 进入菜单模式,选择输入1—9或者数字0。注意在菜单中加入新的代码时要记得吧菜单的数字编号也改了。避免数字对应的算法不一,导致错误的发生。
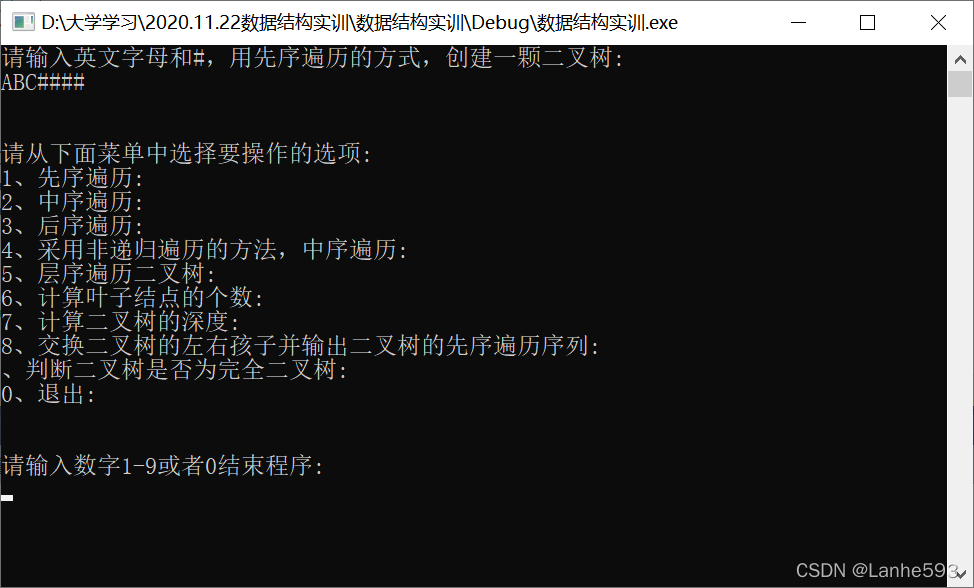
- 输入数字1,先序遍历二叉树。
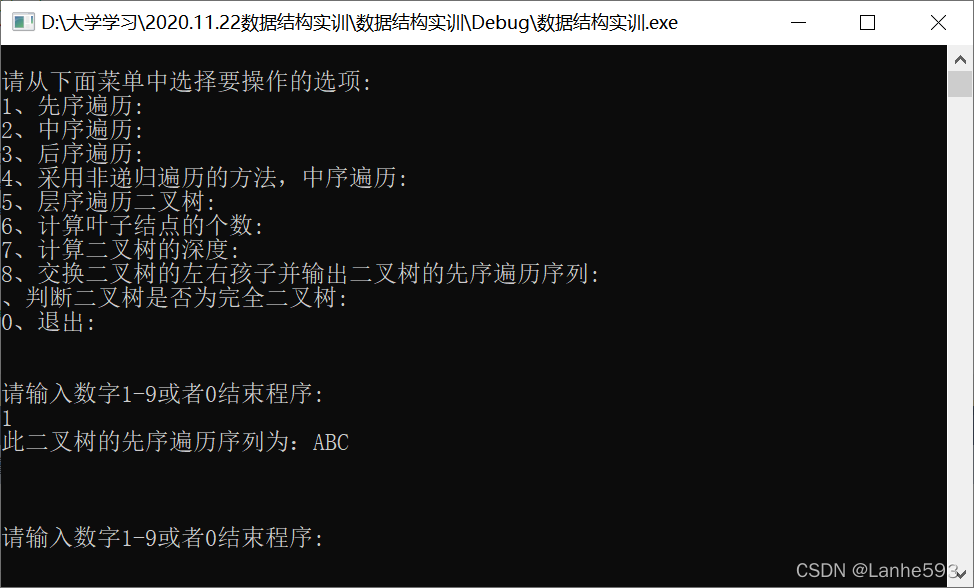
- 输入数字2,中序遍历二叉树。
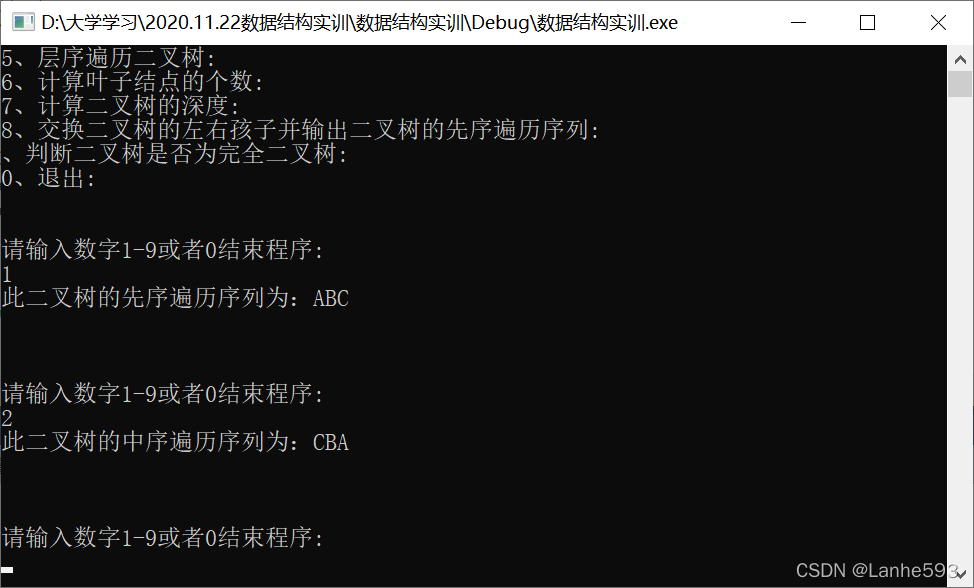
- 输入数字3,后序遍历二叉树。
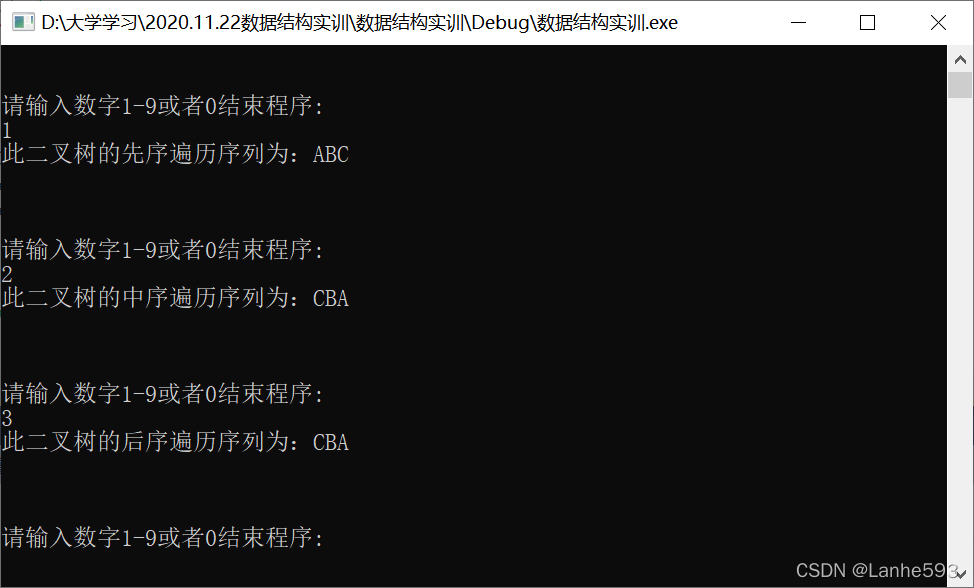
- 输入数字4,非递归中序遍历二叉树。
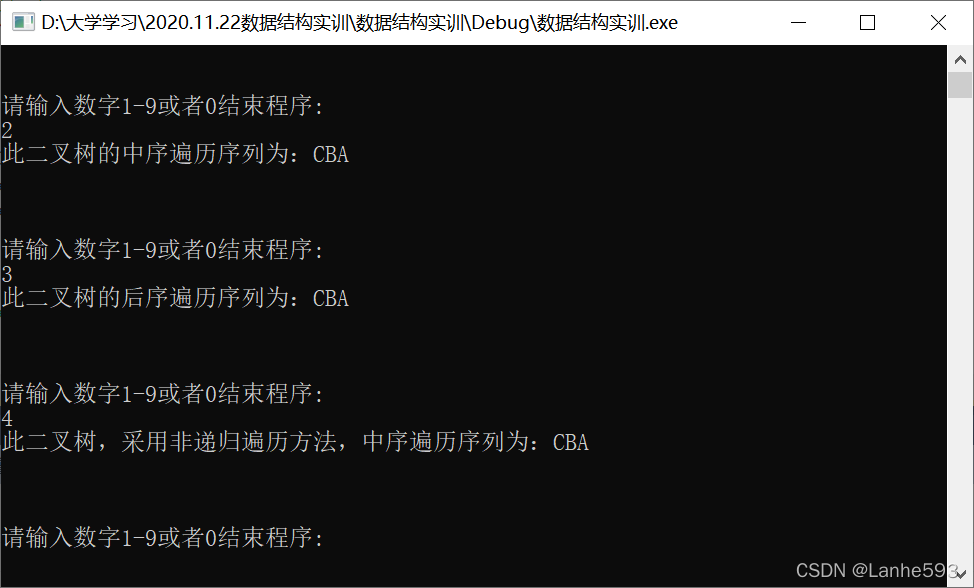
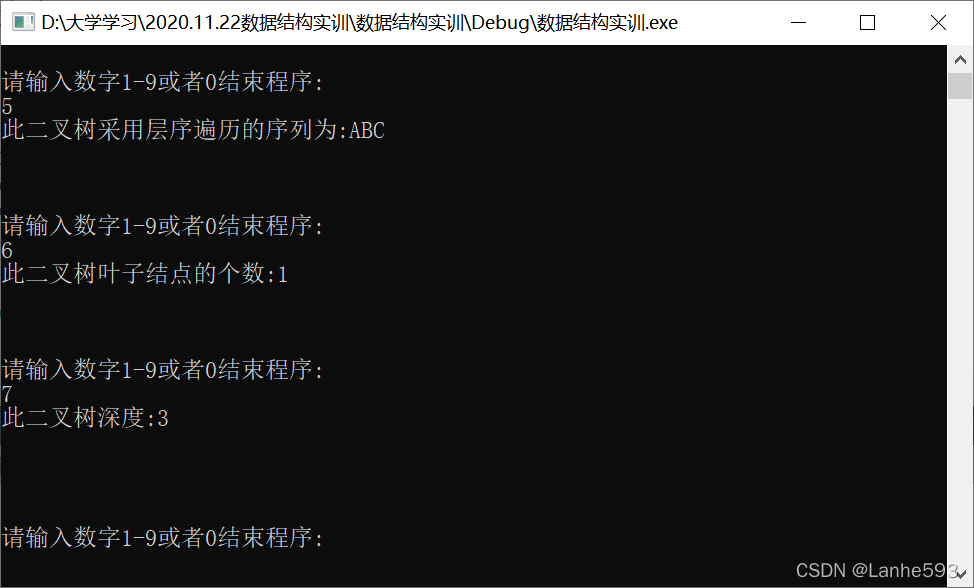
- 输入数字5,层序遍历二叉树。
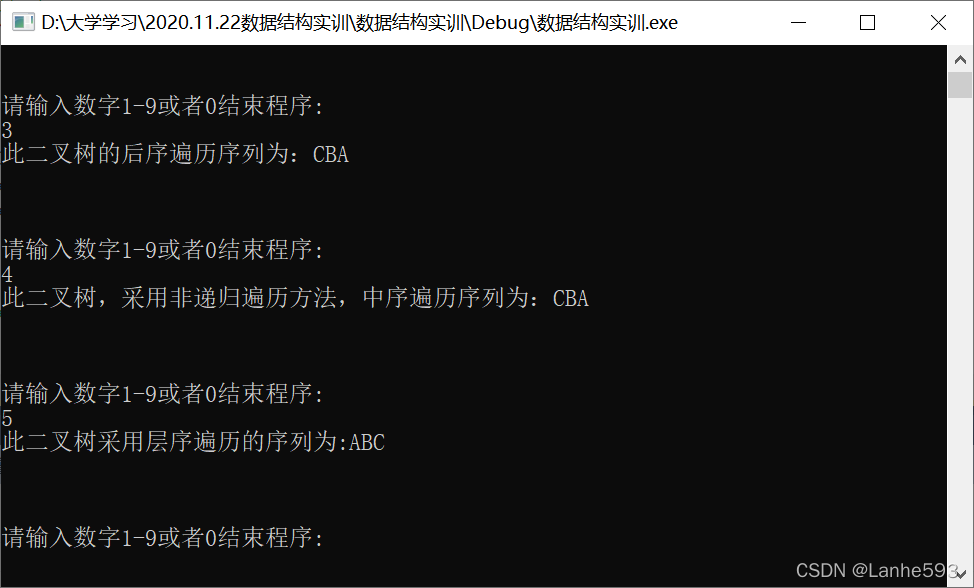
- 输入数字6,计算叶子结点的个数。
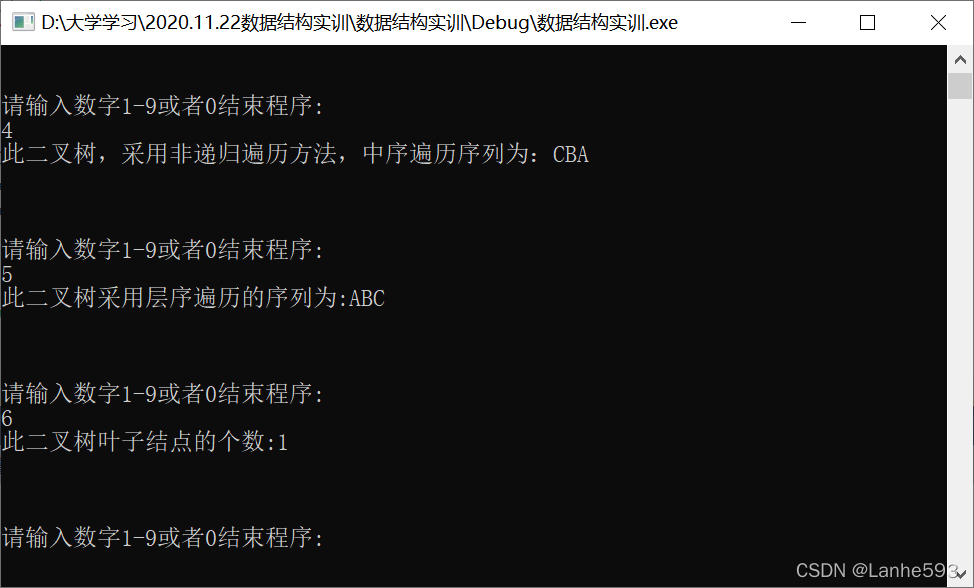
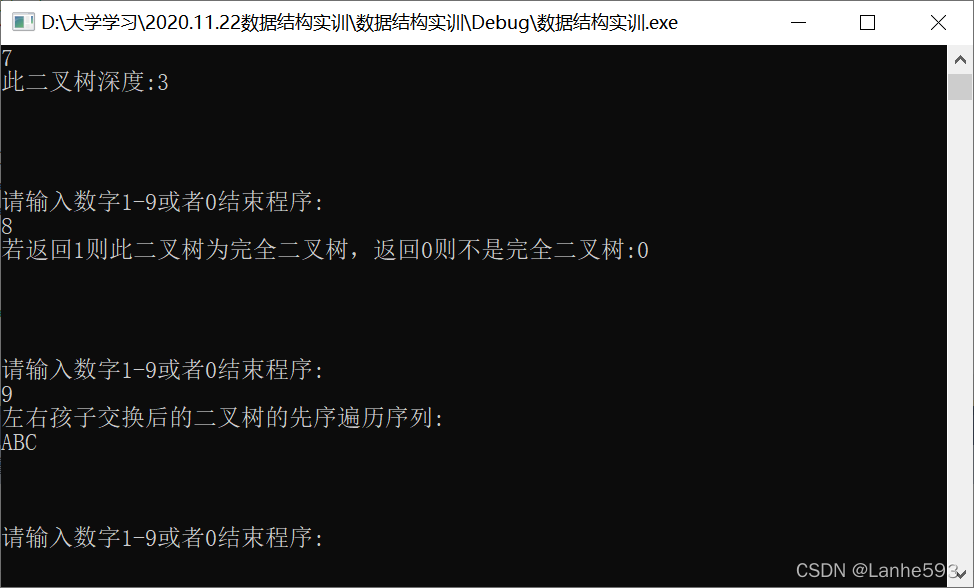
- 输入数字7,计算二叉树的深度。
- 输入数字8,交换二叉树的左右孩子并输出先序遍历序列。
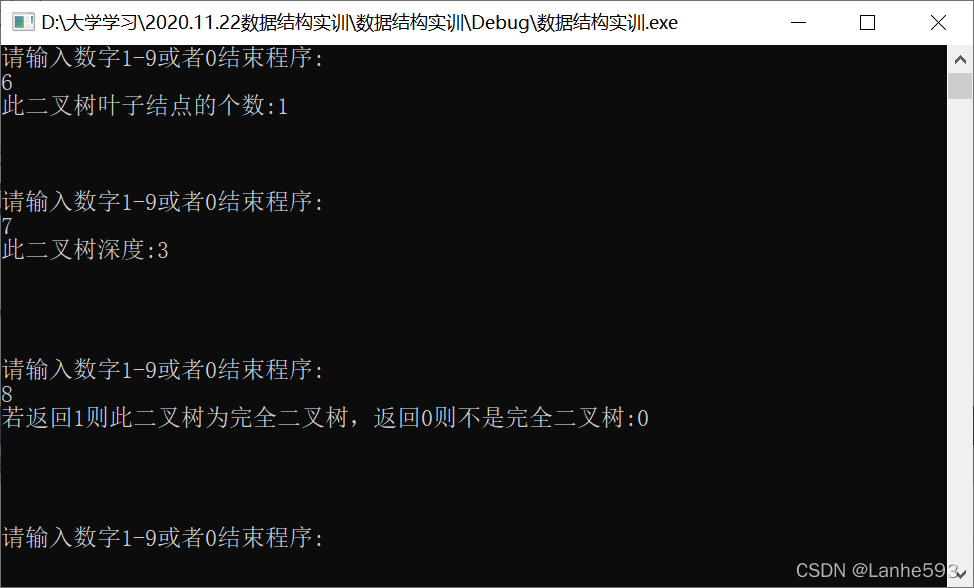
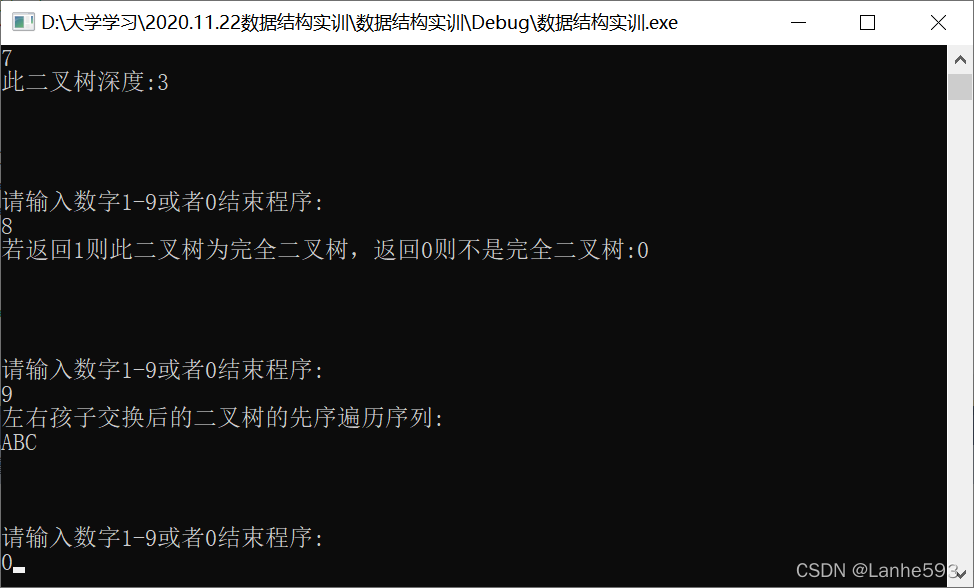
- 输入数字9,判断二叉树是否为完全二叉树,若为完全二叉树则输出1,否则输出0。
- 输入数字0,退出程序,结束运行。
四、实训总结
经过本次实训,对于上机操作有了更加深入的了解和认识。实践和理论知识相比还是有很大的难度的,实训考察的不仅仅是我们的理论知识,更多的是考察我们处理问题的能力和对理论知识的应用能力。丰富的理论知识并不能保证我们能顺利的应用到实践中去,当然,如果我们没有理论知识依然无法实践。实训过程中,我遇到的问题更多的是一些硬件问题,对计算机没有熟悉的认识,不能在电脑出问题时冷静的处理问题。对于实训报告,最大的问题就是我不能熟悉的在电脑上画出流程图。这些问题都充分的说明了无论我们的专业是什么,我们都要全方位的发展,不断充实和完善自己。
此次实训让我认识到了我的很多不足知识之处,也让我对于我的职业生涯规划有了更加清晰的认识。对于计算机这个专业,我有足够的热爱,无论将来会遇到多大的困难,我都要坚持自己的初心,保持良好的心态。今后,我会更加认真的学习理论知识,多进行上机操作,保持一颗向上的心,不断充实自己。
数据结构是一门相当有意思的学科,只要用心就能领悟其中的精华,这是我大学期间的数据结构实训报告,很开心能拿下90+班级第一的好成绩,当然它也耗费了我许多的心血,熬夜掉头发对于现在依然热爱IT行业的我来说仍是家常便饭,但是我不会忘记的初心。大家一起加油吧,哦耶!!!
仅供参考,千万不要抄袭哦哦哦!