公钥加密算法
RSA算法的理论基础:
大素数乘积的因子分解问题,即将两个大素数相乘十分容易,但对其乘积进行因式分解却极其困难,因此可以将乘积作为加密密钥公开(由素数、模运算、费马小定理、欧拉定理、扩展欧几里得算法可进行推导)。
RSA算法流程:
密钥生成方法
1、随机生成两个大的质数p和q,p不等于q,计算N=pq。
2、根据欧拉函数,不大于N且与N互质的整数个数为(p-1)(q-1)。
3、任意选定一个整数e(e不是必须为质数),要求e与(p-1)(q-1)互质,且e小于(p-1)(q-1)。
4、通过公式d×e ≡ 1 (mod (p-1)(q-1))来计算d。
5、将p和q销毁。
6、此时,(N,e)作为公钥使用,(N,d)作为私钥使用。
密钥使用方法
1、接收方在本地生成一对公钥(N,e)和私钥(N,d)。
2、接收方将公钥(N,e)发布到公共空间中,自己留存私钥(N,d)。
3、想要给接收方发送数据的人通过公钥加密数据。
4、接收方收到加密数据后通过私钥解密。
加密方法
1、将消息分组,每组分别加密(即分组加密)。
2、每组消息用以下公式计算:
其中:n为明文,e和N为公钥,余数c为密文。
3、将多组密文组织到一起即形成加密的消息。
解密方法
1、接收方收到加密消息后,将密文分组。
2、每组用以下公式来解码:
其中:c为密文,d和N为私钥,余数n为明文。
3、将每一组明文拼合,得到最终的消息。
例:
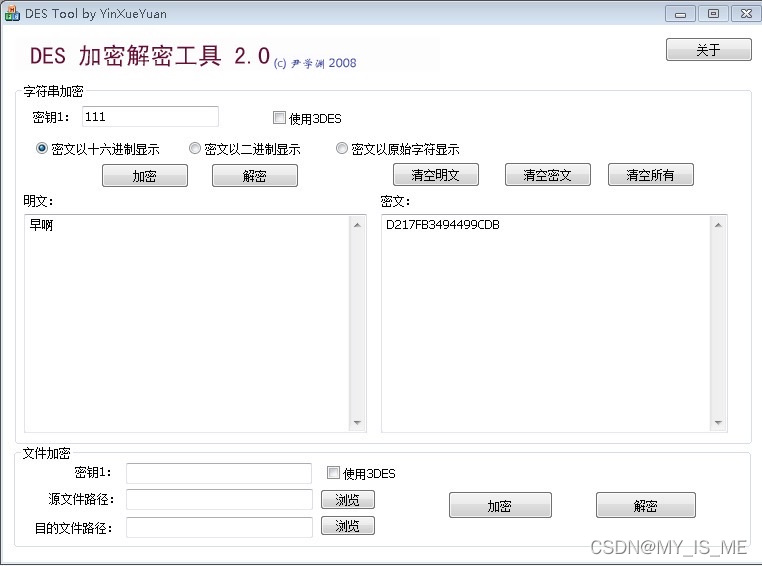
1. 小A同学准备一些文字,选择一
个
密钥利用DES-Too对文字进行加密得到密文1。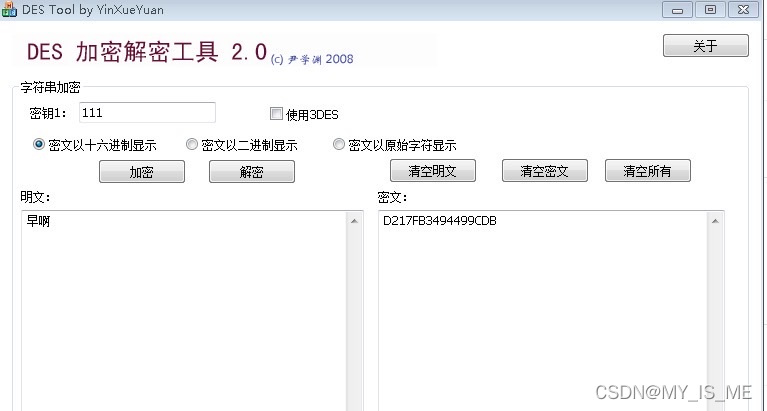
2. 小B同学运行RSA-Tool,生成公钥和私钥,将公钥发送给小A同学,私钥自己留存。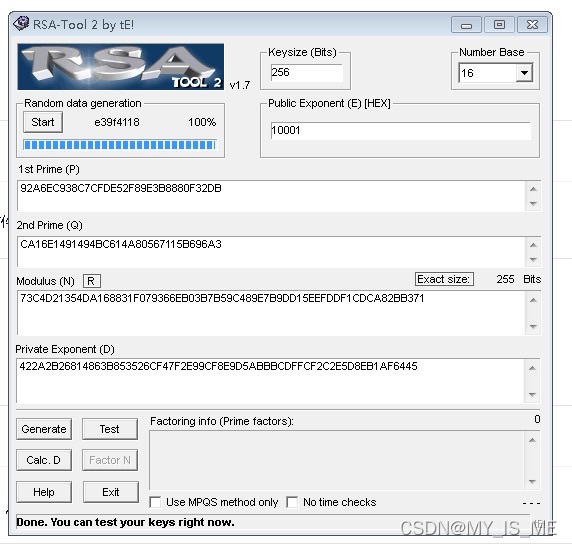
3. 小A同学利用小B同学的公钥对加密信件时使用的对称密钥进行加密,得到密文2。将密文1和密文2一同发送给小B同学
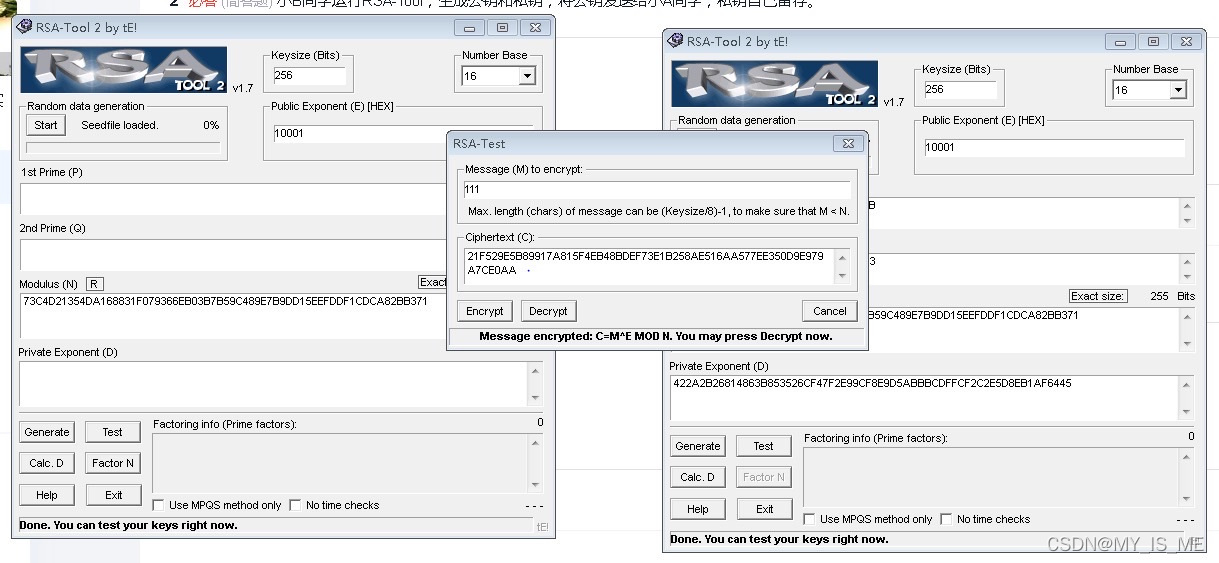
4.小B同学首先用自己的私钥解密密文2,接着利用解密密文2得到的对称密钥在DES-Tool中解密密文1,得到原始文字内容。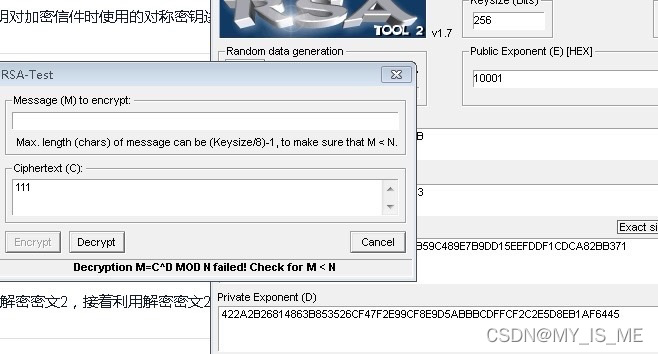
利用RSA算法生成数字签名
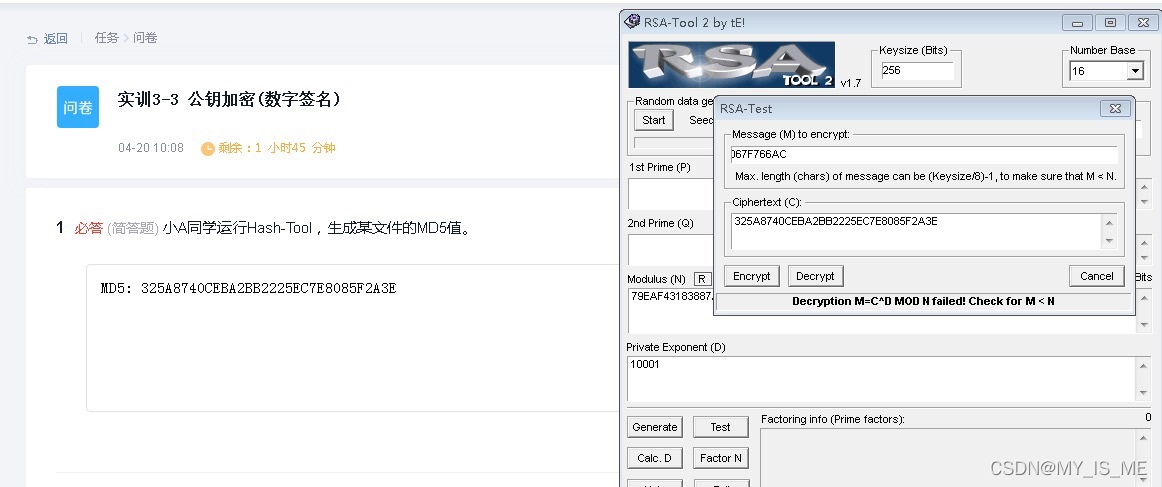
1. 小A同学运行Hash-Tool,生成某文件的MD5值。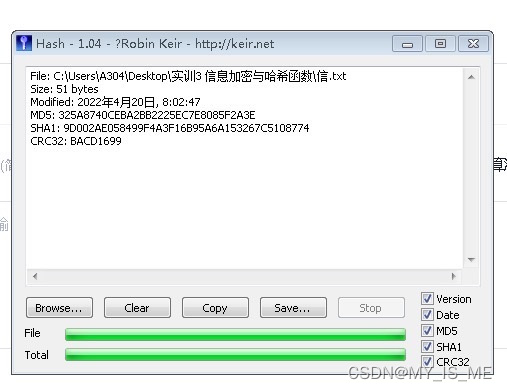
2. 小A同学利用RSA Tool对生成的MD5值进行私钥加密(反向使用RSA算法,Generate生成密钥后将D和E交换位置,再用test进行加密)。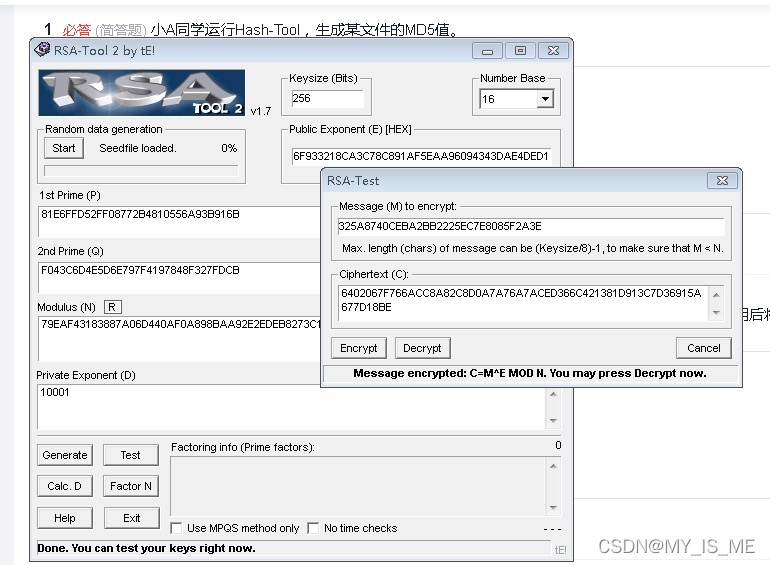
3. 小A同学将公钥、文件和加密后的MD5一起发送给小B同学,由小B同学验证数字签名的正确性(软件中先激活test按钮,再填写公钥进行解密)。