python 余弦相似性_数据挖掘：度量数据的相似性和相异性

本文亮点：使用python实现了书中涉及的标称属性,二元属性,数值属性,序数属性和混合属性的距离计算。talk is cheap, this is my code ，请在我们公众号"数据臭皮匠"后台回复"第二章3"获取本文涉及的代码、思维导图、数据集等资料

在诸如聚类、离群点分析和最近邻分类等数据挖掘应用中,我们需要评估对象之间的相似程度或不相似程度。典型的,相似性值介于0到1之间,如果两个对象i，j完全相同,相似性为1；完全不同,相似性为0,相异性则反之。

由于书中使用的名词相对拗口, 本文使用的名词会与书中有所不同, 比如使用相似性代替临近性, 距离代替相异性等。

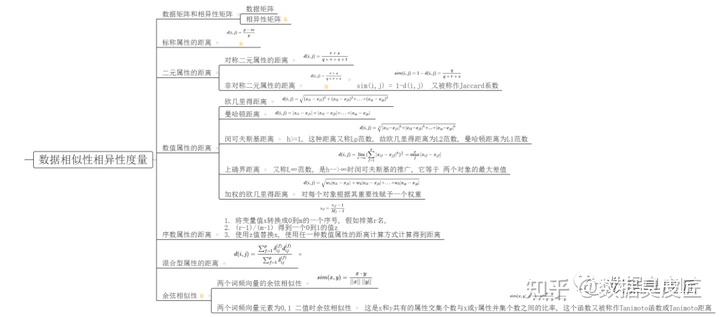
1.数据矩阵和相异性矩阵

假设我们有n个对象,被p个属性(又称维或特征，如年龄、身高、体重或性别）刻画。这些对象是

，

等等，其中

是对象i的第j个属性的值。下文我们称

为对象i。

数据矩阵

具有n个对象p个属性的数据矩阵

相异性矩阵

其中d(i,j) 是对象i和对象j之间的距离(distance) 或称为相异性度量, 一般而言, d(i,j) 是一个非负值, 对象i,j 高度相似时, d(i,j) 接近于0 , 即距离接近于0 且d(i,j) = d(j,i) , 所以下面相异性矩阵只显示对角线左下部分。

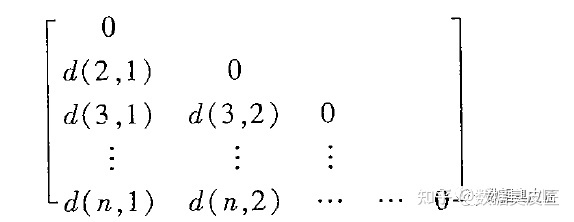
对象i,j的相似性度量sim(i,j)可以表示成相异性度量d(i,j)的函数， 即：

sim(i,j) = 1- d(i,j)

2. 标称属性的相似性度量

在之前的文章（见文末链接第二章2）中，我们讲到了标称属性的定义, 简单讲, 标称属性是枚举型类别变量, 类别间无先后顺序, 如颜色: 红橙黄绿青蓝紫

如何计算标称属性所刻画的对象之间的相异性?

距离：

其中m为对象i,j相同的属性数, p为对象的属性总数(即对象i有p个属性)
计算标称属性距离举例

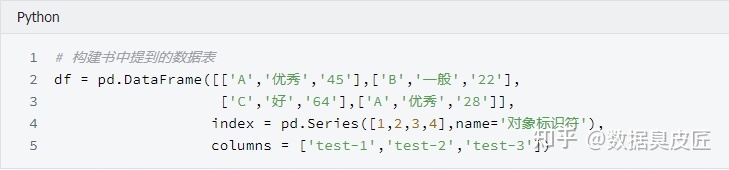
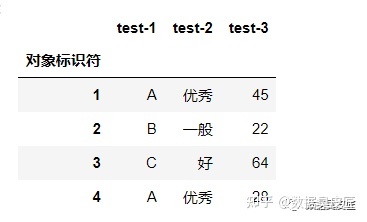
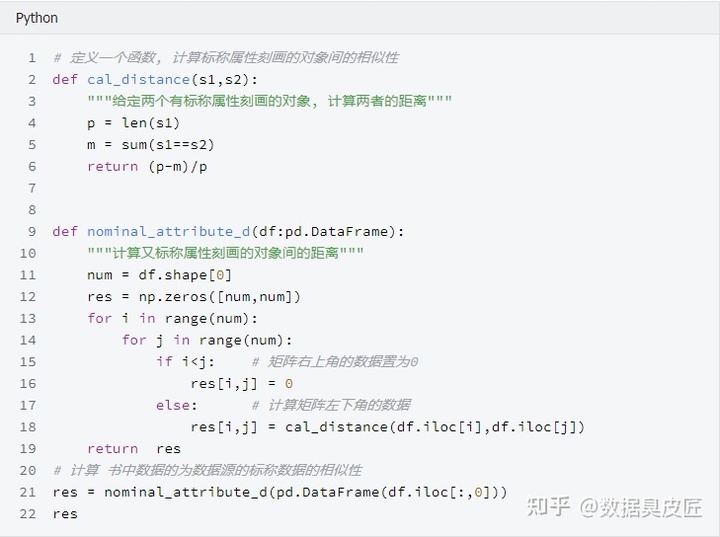
上述计算出的为样本间的距离, 如果需要计算相似性, 则可以用下式计算

sim(i,j) = 1-d(i,j)=m/p

3.二元属性的距离计算

当该属性的值只有0,1 两个值时,称为二元属性, 其实0值和1值有相同的重要性时称为对称二元属性,如性别中的男女, 当0和1有不一样的重要性时, 为非对称二元属性,如是否得癌症, 对二元属性的详细介绍, 请参考我们的上一篇文章 (见文末链接 第二章2）

对称二元属性的距离计算：

非对称二元属性的距离计算：

非对称二元属性的相似性即Jaccard系数计算：

二元属性距离计算举例

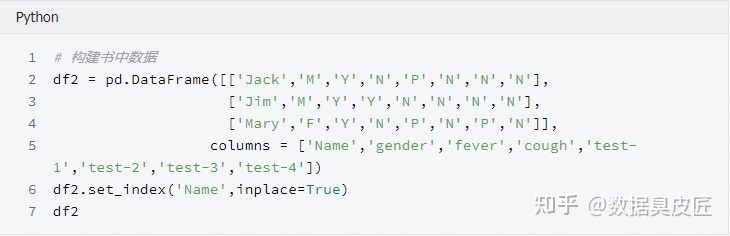
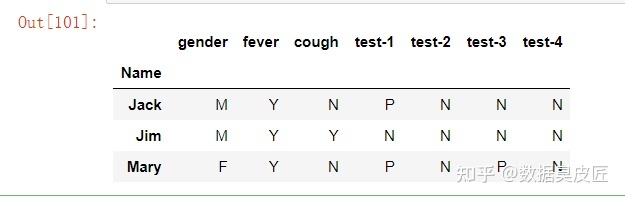
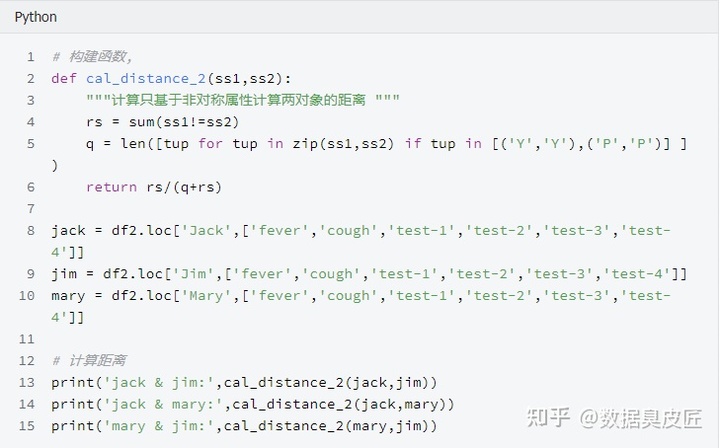
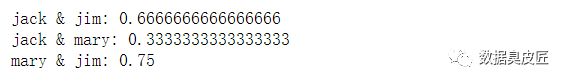
4.数值属性的相异性

欧几里得距离：

曼哈顿距离:

闵可夫斯基距离:

当h=1时, d(i,j) 为L1范数, 即曼哈顿距离 ;当h=2时, d(i,j)为L2范数, 即欧几里得距离

上确界距离:

上确界距离为两对象属性差值最大值的绝对值即:

5.序数属性的距离计算

计算步骤

①: 第i个对象的f值为

,属性有

个有序状态, 表示排位1,2,...Mf, 用对应的

取代

②: 将每个属性的值域映射到[0,1] 上 ，映射公式:

③: 选取4中介绍的任一种数值属性距离计算公式计算距离

序数属性距离计算举例

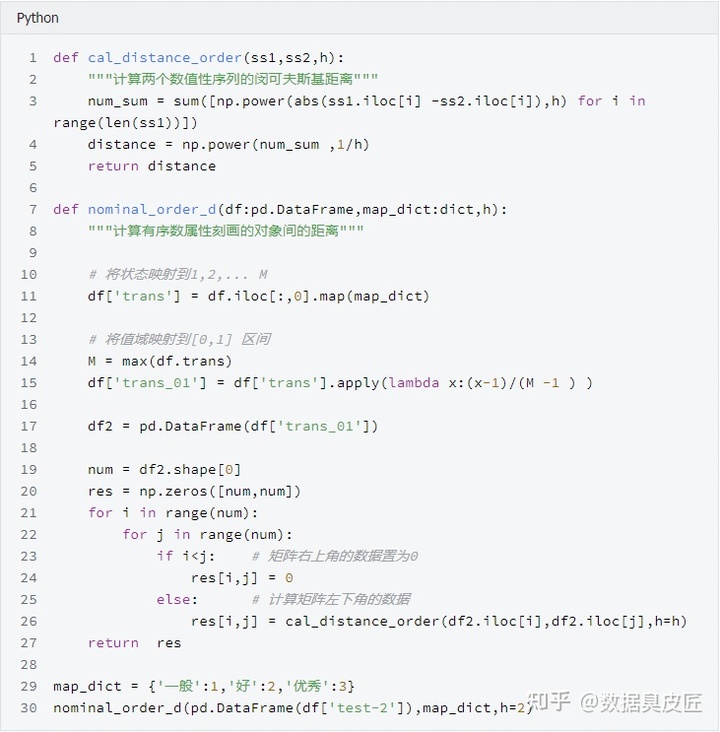
从结果看, 仅使用test-2属性计算距离时,样本1,2 和2,4 的距离为1 , 最不相似, 样本1,4 的距离为0 , 完全相同

6.混合属性的距离

混合属性距离计算的原理和步骤：

其中

或

缺失（即对象i或对象j没有属性f的度量值），或者

且f属性为非对称的二元属性时,

，否则

根据属性的数据类型, 分为三种情况计算距离, 然后求和得到两个样本的距离

① f属性是数值型时:

② f属性为标称或二元元素时,如果

则

,否则

③ f属性为序数时, 先映射为[0,1] 区间的数值, 再按照数值属性对待

混合属性距离计算举例：

7.余弦相似性

余弦相似性一般用来比较两个文档的的相似性, 首先将文档转换为词向量,然后求两个词向量的余弦距离,即为余弦相似性,衡量两个向量有多相似,公式为：

余弦相似性计算举例:

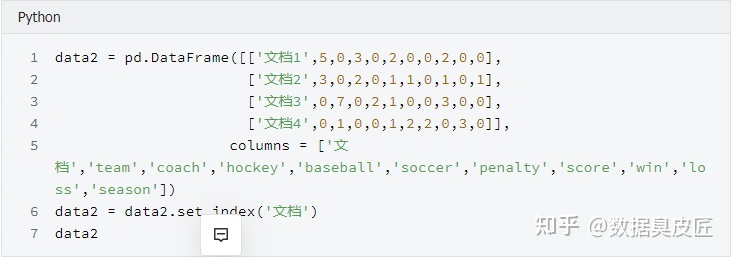
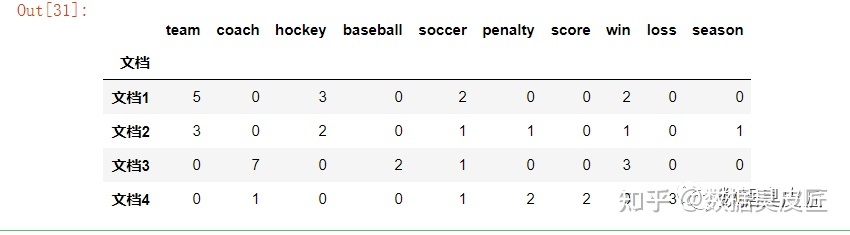
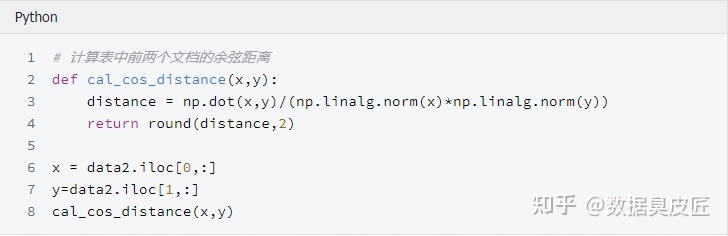
结果为0.94 , 跟书中结果一致,从结果来看, 两个文档是高度相似的 ,

当需要求余弦距离时, d(i,j) = 1-sim(1,j) = 0.06

当词向量值都为二值属性时, 得到余弦相似性的一个简单变种

也被称作Tanimoto系数或Tanimoto距离

数据挖掘概念与技术 第二章 系列文章：

数据挖掘概念与技术 第二章 1

数据挖掘概念与技术 第二章 2

长按公众号关注我们哦(数据臭皮匠)

作者：范小匠

审核：灰灰匠

编辑：森匠