目录
一、机器数
1、计算机采用的数值的表达方式就是机器数;
(1)理解
- 在生活中我们是按十进制计数的,例如10;但是在计算机中是用二进制,这个用于表示十进制数10的二进制的0、1序列,就是机器数。
2、计算机对机器数的约定
- 计算机中约定固定长度的二进制位来表示一个数;
可能是8位,可能是32位,也可能是其他;这个与不同的环境有关,考试的时候需要注意;
- 机器数中约定,用最高为来表示一个数的正负;
0表示正数(+);1表示负数(-);
- 计算机中约定,小数点的位置是固定的;所以机器数中,不需要一位专门的二进制位来表示这个数是小数;
如果是整数,小数点位在最低有效数位之后;
如果是小数的话,小数点在符号位之后,最高有效数位之前;
3、举例说明
(1)8个二进制位表示一个固定的数,那么最高位用来表示正负,剩余7位用来表示数值;
- 1对应的机器数是:0(符号位)0000001;
- -1对应的机器数是:1(符号位)0000001;
- 整数时的小数点位置:0(符号位)0000000.0;
- 小数时的小数点位置:0(符号位).0000000;
二、码制
1、原码
(1)定义
- 原码(true form)是计算机中一种对数字的二进制定点表示方法。
- 可理解为直接由十进制数转换得到的二进制数,就是原码;
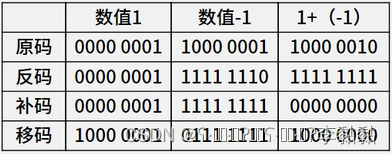
(2)运算
- 由图可知,使用原码来进行二进制数的加减法运算,所得到的结果是错误的;原因是,计算时对原码中的符号位也进行了运算;

(3)正确运算过程
- 将原码中的符号位剔除出来;
- 然后确认减数和被减数的大小,依此来判断计算结果是整数还是负数;
- 然后再进行运算。
2、反码
(1)反码的出现原因
- 按照原码的逻辑进行运算,就复杂了,不利于计算机的实现,所以对于机器数的运算又想出了其他编码方式-反码。
(2)原码和反码的转换
- 正数的原码转反码:不变;
- 负数的原码转反码: 符号位不变;数值位按位取反;
按位取反就是原来是0的位变成1,原来是1的地方变成0;
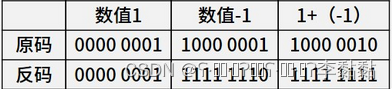
(3)运算
- 由图可知,使用反码来进行二进制数的加减法运算,所得到的结果是错误的;原因也是,计算时对原码中的符号位也进行了运算;
3、补码
(1)补码的出现原因
- 按照反码的逻辑进行运算,就复杂了,不利于计算机的实现,所以对于机器数的运算又想出了其他编码方式-补码。
(2)原码和补码的转换
- 正数的原码转补码:不变;
- 负数的原码转补码: 符号位不变;数值位按位取反后+1;
按位取反就是原来是0的位变成1,原来是1的地方变成0;
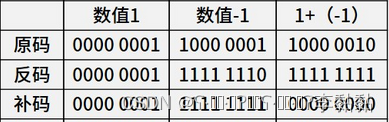
(3)反码和补码的转换
- 整数的补码=反码;
- 负数的补码= 反码+1;
(4)运算
- 由图可知,使用补码来进行二进制数的加减法运算,所得到的结果是正确的;
(5)补码的引用场景
- 用于二进制的加减运算;
4、移码
(1)移码的出现原因
- 通过补码表示浮点数时,可能会出现问题;例如
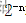 当n无限趋于0的时候,
当n无限趋于0的时候,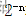 就等于
就等于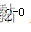 ,就是不正确的;所以用移码来表示浮点数;
,就是不正确的;所以用移码来表示浮点数;
(2)补码和移码的转换
- 正数的移码=补码的符号位取反,其他位不变;
- 负数的移码=补码的符号位取反,其他位不变;
(3)移码的引用场景
- 移码常用于表示浮点数中的阶码。而浮点数的阶码主要决定了浮点数能表示的数值范围。
三、数表示的范围

1、原码
- n位二进制对应的表示编码的个数的计算公式:
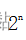 ;
; - n-1:最高位是符号位,只表示数值的正负,不表示数值的大小;表示数值位的二进制位数少了一位,所以需要减去1;
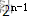 :n位二进制数值,表示的编码个数;
:n位二进制数值,表示的编码个数;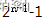 :编码时从0开始编,0~3是四个编码;
:编码时从0开始编,0~3是四个编码;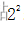 是四个编码,分别是00、01、10、11,其中最大值是3;所以
是四个编码,分别是00、01、10、11,其中最大值是3;所以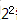 需要再减去1才是最大编码值;所以2n-1-1才能得到最大编码值,才能得到数表示的最大范围;
需要再减去1才是最大编码值;所以2n-1-1才能得到最大编码值,才能得到数表示的最大范围;- 又因为原码的最高位是符号位,说明原码可正可负,所以原码表示的范围有负区间;
2、反码
- 与原码表示的范围一致;
3、补码
- 补码表示的范围的正区间,与原码和反码一致;
- 补码的负区间没有减一,原因是
(1)已知0有两种表示方式:+0=0 0000000;-0=1 00000000;
(2)我们把-0(10000000)用来表示极端的情况,也就是负数的最小的端值,所以负数这一区间内就多出来一个,所以就不用减一了;
4、移码
- 与补码表示的范围一致;
四、考法:数的表示范围


五、各种码制的特点、应用场景

版权声明:本文为qq_46071165原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。