文章目录
析取范式与合取范式
定义
命题变项及其否定的总称
简单析取式
有限个文字构成的析取式
如 p, ¬ \neg¬q, p∨ \vee∨¬ \neg¬q, p∨ \vee∨q∨ \vee∨r, …
析取式
设 p,q为二命题,复合命题“p或q”称作p与q 的析取式,记作p∨ \vee∨q. ∨ \vee∨称作析取联结词,并规定p∨ \vee∨q为假当且仅当p与q同时为假.
简单合取式
有限个文字构成的合取式
如p,¬ \neg¬q,p∧ \wedge∧¬ \neg¬q,p∧ \wedge∧q∧ \wedge∧r,…
合取式
设p,q为二命题,复合命题“p并且q”(或“p与q”)称为p与q的合取式,记作p∧ \wedge∧q. ∧ \wedge∧称作合取联结词,并规定 p∧ \wedge∧q为真当且仅当p与q同时为真。
析取范式
由有限个简单合取式组成的析取式A1∨ \vee∨A2∨ \vee∨…∨ \vee∨Ar,其中,A1,A2,…Ar是简单合取式
合取范式
由有限个简单析取范式组成的合取式A1
∧ \wedge∧A2∧ \wedge∧…∧ \wedge∧Ar,其中A1,A2,Ar是简单析取式
范式
析取范式与合取范式的总称
公式A的析取范式
与A等值的析取范式
公式A的合取范式
与A等值的合取范式
说明:单个文字既是简单析取式,又是简单合取式
命题公式的范式
定理:任何命题公式都存在着与之等值的析取范式与合取范式。
求公式A的范式的步骤
- 消去A中的->,<->(若存在)
- 否定连接词¬ \neg¬的内移或消去
- 使用分配律
∧ \wedge∧对∨ \vee∨分配(析取范式)
∨ \vee∨对∧ \wedge∧分配(合取范式)
公式的范式存在,但不唯一。
求公式的范式举例
求下列公式的析取范式与合取范式
(1) A=(p->¬ \neg¬q)∨ \vee∨¬ \neg¬r
解:
(p->¬ \neg¬q)∨ \vee∨¬ \neg¬r
<=>(¬ \neg¬p∨ \vee∨¬ \neg¬q)∨ \vee∨¬ \neg¬r (消去->)
<=>¬ \neg¬p∨ \vee∨¬ \neg¬q∨ \vee∨¬ \neg¬r(结合律)
这既是A的析取范式(由三个简单的合取式组成的析取式),又是A的合取范式(由一个简单析取式组成的合取式)
(2) B=(p->¬ \neg¬q)->r
解 (p->¬ \neg¬q)->r
<=>(¬ \neg¬p∨ \vee∨¬ \neg¬q)->r (消去第一个->)
<=>¬ \neg¬(¬ \neg¬p∨ \vee∨¬ \neg¬q)∨ \vee∨r (消去第二个->)
<=>(p∧ \wedge∧q)∨ \vee∨r (否定号内移–德·摩根律)
这一步已为析取范式(两个简单合取式构成)
继续:
(p∧ \wedge∧q)∨ \vee∨r
<=>(p∨ \vee∨r)∧ \wedge∧(q∨ \vee∨r) (∨ \vee∨对∧ \wedge∧分配律)
这一步得到合取范式(由两个简单析取式构成)
极大项与极小项
定义
在含有n个命题变项的简单合取式(简单析取式)中,若每个命题变项均以文字的形式出现且仅出现一次,称这样的简单合取式(简单析取式)为极小项(极大项)
说明
- n个命题变项产生2n个极小项和2n个极大项
- 2^n个极小项(极大项)均互不等值
- 在极小项和极大项中文字均按下标或字母顺序排序
- 用mⅰ表示第ⅰ个极小项,其中i是该极小项成真赋值的十进制表示。用Mⅰ表示第ⅰ个极大项,其中ⅰ是该极大项成假赋值的十进制表示,mⅰ(Mⅰ)称为极小项(极大项)的名称
- mⅰ与Mⅰ的关系:¬ \neg¬mⅰ<=>Mⅰ,¬ \neg¬Mⅰ<=>mⅰ
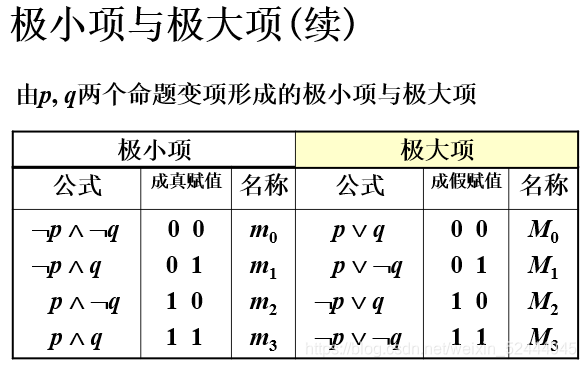
由p,q两个命题变项形成的极小项与极大项
| 极小项 | 极大项 | ||
|---|---|---|---|
| 公式 | 成真赋值 | 名称 | 公式 |
| ¬ \neg¬p∧ \wedge∧¬ \neg¬q | 0 0 | m0 | p∨ \vee∨q |
| ¬ \neg¬p∧ \wedge∧q | 0 1 | m1 | p∨ \vee∨¬ \neg¬q |
| p∧ \wedge∧¬ \neg¬q | 1 0 | m2 | ¬ \neg¬p∨ \vee∨q |
| p∧ \wedge∧q | 1 1 | m3 | ¬ \neg¬p∨ \vee∨¬ \neg¬q |
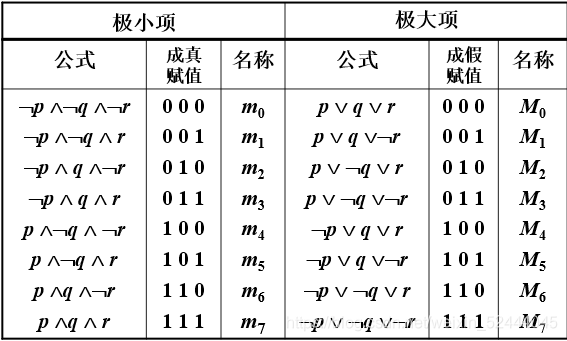
由p, q, r三个命题变项形成的极小项与极大项
主析取范式与主合取范式
主析取范式
由极小项构成的析取范式
主合取范式
由极大项构成的合取范式
举个例子
当n=3,命题变项为p,q,r时,
(¬ \neg¬p∧ \wedge∧¬ \neg¬q∧ \wedge∧r)∨ \vee∨<=>m1∨ \vee∨m3是主析取范式
(p∨ \vee∨q∨ \vee∨¬ \neg¬r)KaTeX parse error: Undefined control sequence: \dewge at position 1: \̲d̲e̲w̲g̲e̲(¬ \neg¬p∨ \vee∨q∨ \vee∨¬ \neg¬r)<=>M1KaTeX parse error: Undefined control sequence: \dewge at position 1: \̲d̲e̲w̲g̲e̲M5是主合取范式
A的主析取范式
与A等值的主析取范式
A的主合取范式
与A等值的主合取范式
定理
任何命题公式都存在着与之等值的主析取范式和主合取范式,并且是唯一的。
求公式的主范式
用等值演算法求公式的主范式的步骤
- 先求析取范式(合取范式)
- 将不是极小项(极大项)的简单合取式(简单析取式)化为与之等值的若干个极小项的析取(极大项的合取),需要利用同一律(零律)、排中律(矛盾律)、分配律、幂等律等。
- 极小项(极大项)用名称mi(Mi)表示,并按角标 从小到大顺序排序。
例题
例1 求公式A=(p->¬ \neg¬q)->r的主析取范式与主合取范式
(1)求主析取范式
(p->¬ \neg¬q)->r
<=>(p∧ \wedge∧q)∨ \vee∨r (析取范式) ①
(p∧ \wedge∧q)
<=>(p∧ \wedge∧q)∧ \wedge∧(¬ \neg¬r∨ \vee∨r)
<=>(p∧ \wedge∧q∧ \wedge∧¬ \neg¬r)∨ \vee∨(p∧ \wedge∧q∧ \wedge∧r)
<=>m6∨ \vee∨m7 ②
r
<=>(¬ \neg¬p∨ \vee∨p)∧ \wedge∧(¬ \neg¬q∨ \vee∨q)∧ \wedge∧r
<=>(¬ \neg¬p∧ \wedge∧¬ \neg¬q∧ \wedge∧r)∨ \vee∨(¬ \neg¬p∧ \wedge∧q∧ \wedge∧r)∨ \vee∨(p∧ \wedge∧¬ \neg¬q∧ \wedge∧r)∨ \vee∨(p∧ \wedge∧q∧ \wedge∧r)
<=>m1∨ \vee∨m3∨ \vee∨m5∨ \vee∨m7 ③
②,③代入①并排序,得
(p->¬ \neg¬q)->r<=>m1∨ \vee∨m3∨ \vee∨m5∨ \vee∨m6∨ \vee∨m7 (主析取范式)
(2)求A的主合取范式
(p->¬ \neg¬q)->r
<=>(p∨ \vee∨r)∧ \wedge∧(q∨ \vee∨r) (合取范式) ①
p∨ \vee∨r
<=>p∨ \vee∨(q∧ \wedge∧¬ \neg¬q)∨ \vee∨r
<=>M0∧ \wedge∧M2 ②
q∨ \vee∨r
<=>(p∧ \wedge∧¬ \neg¬p)∨ \vee∨q∨ \vee∨r
<=>(p∨ \vee∨q∨ \vee∨r)∧ \wedge∧(¬ \neg¬p∨ \vee∨q∨ \vee∨r)
<=>M0∧ \wedge∧M4 ③
②,③代入①并排序,得
(p->¬ \neg¬q)->r<=>M0∧ \wedge∧M2∧ \wedge∧M4 (主合取范式)
主范式的用途–与真值表相同
(1)求公式的成真赋值和成假赋值

(2)判断公式的类型

(3)判断两个公式是否等值

(4)

解此类问题的步骤为:
- 将简单命题符号化
- 写出各复合命题
- 写出由2.中复合命题组成的合取式
- 求3.中所得公式的主析取范式


