15分钟学会ARIMA-基于R语言

ARIMA，AR是指auto regressive，MA，是指Moving Average，中间的I是指差分。
下面介绍如何用很少的代码对序列实现预测，以《时间序列分析-基于R》第五章习题5.1为例，下面五句代码实现了建模，画图，预测的所有ARIMA功能。

library(forecast)#载入forecast包
exer5.1 <- ts(a,start = 1949)#a是铁路货运量数据，生成时间序列
plot(exer5.1)#画出折线图
fit5.1<-auto.arima(exer5.1)#执行自动ARIMA，建立模型
forecast(fit5.1,h=5)#用预测函数预测后五年的铁路货运量

自此题目已经做完。让我们进一步分析下每句语句。

1.生成时间序列

exer5.1 <- ts(a,start = 1949)#a是铁路货运量数据，生成时间序列
#生成时间序列，如下
Time Series:
Start = 1949 
End = 2008 
Frequency = 1 
 [1]   5589   9983  11083  13217  16131  19288  19376  24605  27421  38109
[11]  54410  67219  44988  35261  36418  41786  49100  54951  43089  42095
[21]  53120  68132  76471  80873  83111  78772  88955  84066  95309 110119
[31] 111893 111279 107673 113495 118784 124074 130709 135635 140653 144948
[41] 151489 150681 152893 157627 162794 163216 165982 171024 172149 164309
[51] 167554 178581 193189 204956 224248 249017 269296 288224 314237 330354

2.自动生成ARIMA模型

fit5.1<-auto.arima(exer5.1)#执行自动ARIMA，建立模型
fit5.1
#以下是生成的结果
Series: exer5.1 
ARIMA(0,2,2) 

Coefficients:
          ma1      ma2
      -0.4427  -0.3315
s.e.   0.1190   0.1212

sigma^2 estimated as 55215220:  log likelihood=-598.66
AIC=1203.32   AICc=1203.77   BIC=1209.5

3.对生成ARIMA模型进行预测

fore5<-forecast(fit5.1,h=5);fore5
plot(fore5)
#运行结果

Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
2009       344539.9 335017.1 354062.7 329976.0 359103.8
2010       359930.8 342306.4 377555.1 332976.7 386884.9
2011       375321.7 350848.2 399795.2 337892.7 412750.7
2012       390712.6 359649.2 421776.1 343205.1 438220.1
2013       406103.5 368449.6 443757.5 348516.7 463690.3

预测给出了，预测值，已经上下80%置信区间，和95%置信区间，并且我们直接用plot函数，画出示意图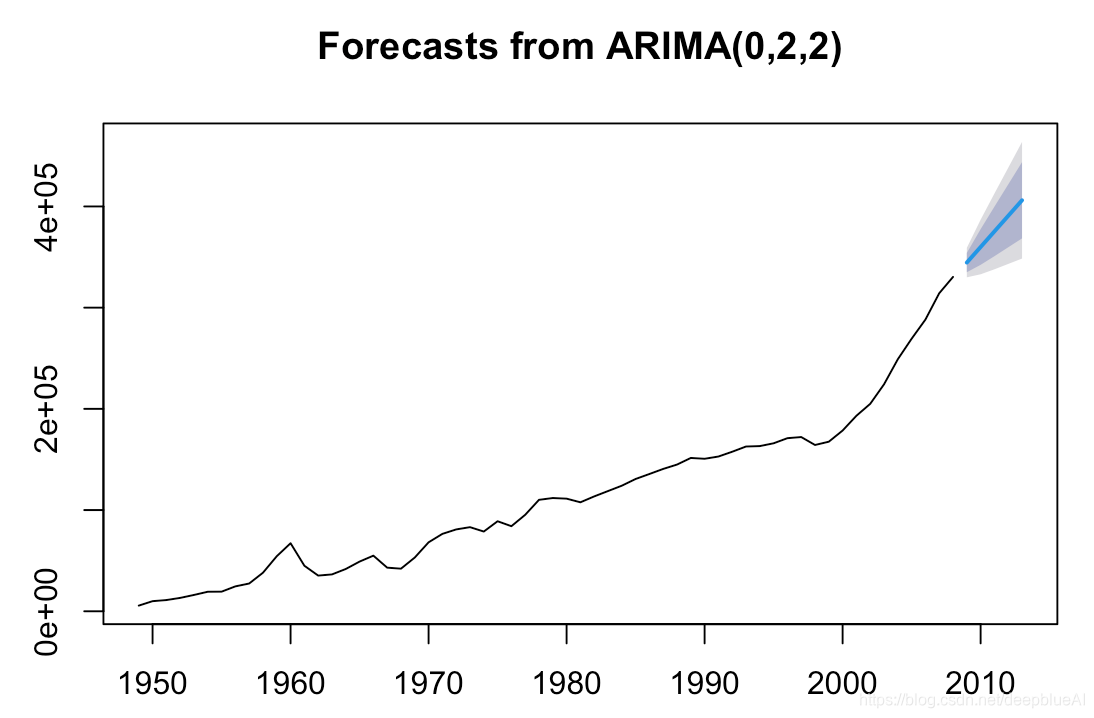

自此，解题完成。这样做可以吗？正确但不严谨，也不符合我们一般做法。如果只是想完成简单的预测问题不想深究，那也可以满足需求了。下面我们就来说下传统的做法。

主要做两件事情：
1.判断序列是否平稳，是否非白噪声
2.通过观测ACF图与PACF图确定ARIMA模型的参数

1.看时序图
如上图，去除最后预测部分，就是时序图，图呈现明显的上升趋势，所以序列显著非平稳，需要做一次差分

exer5.1d<-  diff(exer5.1)#做一次差分
plot(exer5.1d)#画出差分后图形
adf.test(exer5.1d)#测试是否为平稳序列，p值>0.05，不拒绝非平稳，它还是一个非平稳序列
Box.test(exer5.1d,lag = 6,type = 'Ljung-Box')#测试是否非白噪声，测试通过，不是白噪声
##一阶差分后，序列满足非白噪声，但不满足平稳性

##注意序列需要满足平稳，以及非白噪声（即不是随机序列）
##二阶差分后，序列满足平稳性，但是不满足非白噪声
#所以现在没法继续做下去了，白噪声序列不具有研究意义，现在只有两个选择，要么睁一只闭一只眼，继续拟合ARIMA模型，寻找AIC最小的模型，并且判断残差是否为白噪声，要么用其他模型来拟合
#例如holtwinters（）
#或者取log后进行lm（）拟合

解题完毕，你是否会选择一开始五行代码作为你的解题方法吗？