卷积

若输入含有多个通道，则对于某个卷积核，分别对每个通道求feature map后将对应位置相加得到最终的feature map，如下图所示：
若有多个卷积核，则对应多个feature map，也就是下一个输入层有多个通道。如下图所示：

图像上采样的三种方法：上采样指的是任何可以让图像变成更高分辨率的技术

方法一 ：反卷积

（1）正常卷积
在介绍反卷积之前，我们需要深入了解一下卷积，一个简单的卷积层运算，卷积参数为$i=4,k=3,s=1,p=0$,如下图所示。

对于上述卷积运算，我们把上图所示的3×3卷积核展成一个如下所示的[4,16]的稀疏矩阵C，如下：
我们再把4×4的输入特征展成[16,1]的矩阵 X

那么 Y=CX则是一个[4,1]的输出特征矩阵，把它重新排列2×2（reshape成 2∗2）的矩阵

从上述分析可以看出卷积层的计算其实是可以转化成矩阵相乘的。值得注意的是，在一些深度学习网络的开源框架中并不是通过这种这个转换方法来计算卷积的，因为这个转换会存在很多无用的0乘操作。

通过上述的分析，我们已经知道卷积层的前向操作可以表示为和矩阵C相乘，很容易得到卷积层的反向传播就是和C的转置相乘。

（2）反卷积

我们已经说过反卷积又被称为Transposed(转置) Convolution，
我们可以看出其实卷积层的前向传播过程就是反卷积层的反向传播过程，卷积层的反向传播过程就是反卷积层的前向传播过程。
因为卷积层的前向反向计算分别为乘$C$和 $C^T$
(前向传播Y=CX) ------------- 反向传播Y=$C^T$X）

而反卷积层的前向反向计算分别为乘 $C^T$和 $(C^T{)}^T$
（前向传播Y=$C^T$X）—（反向传播Y=$(C^T{)}^T$X）

所以它们的前向传播和反向传播刚好交换过来。

下图表示一个和上图卷积计算对应的反卷积操作，其中他们的输入输出关系正好相反。如果不考虑通道以卷积运算的反向运算来计算反卷积运算的话，还可以通过离散卷积的方法来求反卷积。

如下图所示，不同大小的特征图反卷积的结果，如图b、d、f、h、j 红色框出来的。

图c、e、g、i是不同featrue map大小的UnPooling结果。

可以直观的感受一下，不同上采样让图像变成更高分辨率的效果。

方法二：反池化（上池化Unpooling）

池化操作中最常见的最大池化和平均池化，因此最常见的反池化操作有反最大池化和反平均池化，其示意图如下：

反最大池化需要记录池化时最大值的位置，反平均池化不需要此过程。

方法三：插值

插值就是在不生成像素的情况下增加图像像素大小的一种方法，在周围像素色彩的基础上用数学公式计算丢失像素的色彩（也有的有些相机使用插值，人为地增加图像的分辨率）。所以在放大图像时，图像看上去会比较平滑、干净。但必须注意的是插值并不能增加图像信息。

1. 插值 - 线性 (linear)

根据图中的假设：已知点(x0,y0)、(x1,y1)，试问在x处插值，y的值是多少？用我们初中学过的知识，已知两个点的坐标可以得到一条线，又已知线上一点的一个坐标可以求得这个点的另一个坐标值。这就是线性插值的原理。x只是表示的相对的位置，y才是我们想要的结果：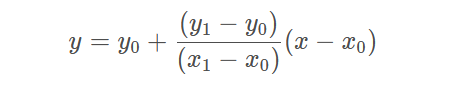

说白了就是线性函数 比如1 和 3之间线性插值 肯定就是2 了

2. 插值 - 双线性 (bilinear)

我们的目标是得到未知函数f在绿色点P(x,y)的像素值，已知Q11(x1,y1)、Q12(x1,y2)、Q21(x2,y1)、Q22(x2,y2)的坐标以及对应的像素值。首先在x方向进行插值，得到R1和R2，然后在y方向进行插值，得到P，这就是整个的数学计算思路。

3. 插值 - 最邻近元法（Nearest Neighbour Interpolation）

这是最简单的一种插值方法，不需要计算，在待求像素的四邻像素中，将距离待求像素最近的邻像素灰度赋给待求像素。更简单了，连计算都不计算了，直接填。