Fisher线性判别分析(LDA)
参考文献:【python3 Fisher线性判别分析(LDA)(含详细推导和代码)】
1. 前言
两类的线性判别问题可以看作是把所有样本都投影到一个方向上,然后在这个一维空间中确定一个分类的阈值。过这个阈值点且与投影方向垂直的超平面就是两类的分类面。
Fisher线性判别分析(LDA)的思想是:
选择投影方向,使投影后两类相隔尽可能远,而且同时每一类内部的样本又尽可能聚集。
2. 基本概念
训练样本集是X = { x 1 , . . . , x N } X=\{x_1,...,x_N\}X={x1,...,xN},每个样本是一个d dd维向量,其中w 1 w_1w1类的样本X 1 = { x 1 1 , . . . , x N 1 1 } X_1=\{x_1^1,...,x_{N_1}^1\}X1={x11,...,xN11},w 2 w_2w2类的样本是X 2 = { x 1 2 , . . . , x N 2 2 } X_2=\{x_1^2,...,x_{N_2}^2\}X2={x12,...,xN22}。目的是寻找一个投影方向w ww,投影以后的样本变成:
y i = w T x i , i = 1 , 2 , . . . , N (1) y_i=w^T x_i,i=1,2,...,N \tag 1yi=wTxi,i=1,2,...,N(1)
2.1 原样本空间
类的均值向量:
m i = 1 N ∑ x j ∈ X i x j , i = 1 , 2 (2) m_i=\frac{1}{N} \sum_{x_j \in X_i} x_j,i=1,2 \tag 2mi=N1xj∈Xi∑xj,i=1,2(2)
各类的类内离散度矩阵:
S i = ∑ x j ∈ X i ( x j − m i ) ( x j − m i ) T , i = 1 , 2 (3) S_i=\sum_{x_j \in X_i} (x_j-m_i)(x_j-m_i)^T,i=1,2 \tag 3Si=xj∈Xi∑(xj−mi)(xj−mi)T,i=1,2(3)
总类内离散度矩阵:
S w = S 1 + S 2 (4) S_w=S_1+S_2 \tag 4Sw=S1+S2(4)
类间离散度矩阵:
S b = ( m 1 − m 2 ) ( m 1 − m 2 ) T (5) S_b=(m_1-m_2)(m_1-m_2)^T \tag 5Sb=(m1−m2)(m1−m2)T(5)
2.2 投影以后的一维空间
两类的均值:
m i ~ = 1 N i ∑ y j ∈ Y i y i = 1 N i ∑ x j ∈ X i w T x j = w T m i , i = 1 , 2 (6) \widetilde{m_i}=\frac{1}{N_i} \sum_{y_j \in Y_i} y_i=\frac{1}{N_i} \sum_{x_j \in X_i} w^Tx_j=w^T m_i,i=1,2 \tag 6mi=Ni1yj∈Yi∑yi=Ni1xj∈Xi∑wTxj=wTmi,i=1,2(6)
类内离散度:
S i ~ 2 = ∑ y j ∈ Y i ( y j − m i ~ ) 2 (7) \widetilde{S_i}^2=\sum_{y_j \in Y_i} (y_j- \widetilde{m_i})^2 \tag 7Si2=yj∈Yi∑(yj−mi)2(7)
总类内离散度:
S w ~ = S 1 ~ 2 + S 2 ~ 2 (8) \widetilde{S_w}=\widetilde{S_1}^2+\widetilde{S_2}^2 \tag 8Sw=S12+S22(8)
类间离散度:
S b ~ 2 = ( m 1 ~ − m 2 ~ ) 2 (9) \widetilde{S_b}^2=(\widetilde{m_1}-\widetilde{m_2})^2 \tag 9Sb2=(m1−m2)2(9)
根据LDA的目的,可以将这一目标表示成如下的准则:
max J F ( w ) = S b ~ S w ~ = ( m 1 ~ − m 2 ~ ) 2 S 1 ~ 2 + S 2 ~ 2 (10) \max \ J_F(w)=\frac{\widetilde{S_b}}{\widetilde{S_w}}=\frac{(\widetilde{m_1}-\widetilde{m_2})^2}{\widetilde{S_1}^2+\widetilde{S_2}^2} \tag {10}max JF(w)=SwSb=S12+S22(m1−m2)2(10)
Fisher准则函数(Fisher‘s Criterion)
根据上述式子对S b ~ \widetilde{S_b}Sb和S w ~ \widetilde{S_w}Sw化简有:
S b ~ = w T S b w , S w ~ = w T S w w (11) \widetilde{S_b}=w^TS_bw,\widetilde{S_w}=w^TS_ww \tag {11}Sb=wTSbw,Sw=wTSww(11)
此时( 11 ) (11)(11)式转化为:
max w J F ( w ) = w T S b w w T S w w (12) \max_{w} \ J_F(w)=\frac{w^TS_bw}{w^TS_ww} \tag {12}wmax JF(w)=wTSwwwTSbw(12)
该式在数学物理中被称作广义Rayleigh商。
3. 最大投影方向的求解
既然目的是为了求解最大的投影方向w ww。由于对w ww幅值的条件不会影响w ww的方向,即不会影响J F ( w ) J_F(w)JF(w)的值。因此设定式( 12 ) (12)(12)的分母为非零常数而最大化分子部分,即把式( 12 ) (12)(12)的优化问题转化为:
max w T S b w s . t . w T S w w = c ≠ 0 (13) \max \ w^TS_bw \\ s.t. \ w^TS_ww=c\not=0 \tag {13}max wTSbws.t. wTSww=c=0(13)
这是一个等式约束下的极值问题。可以通过引入拉格朗日乘子转化成以下拉格朗日函数的无约束极值问题:
L ( w , λ ) = w T S b w − λ ( w T S w w − c ) (14) L(w,\lambda)=w^TS_bw-\lambda(w^TS_ww-c) \tag {14}L(w,λ)=wTSbw−λ(wTSww−c)(14)
对w ww求偏导,在极值处应该满足:
∂ ( w , λ ) ∂ w = 0 (15) \frac{\partial(w,\lambda)}{\partial w}=0 \tag {15}∂w∂(w,λ)=0(15)
由此可得,极值解w ∗ w^{*}w∗应满足:
S b w ∗ − λ S w w ∗ = 0 (16) S_bw^{*}-\lambda S_ww^{*}=0 \tag {16}Sbw∗−λSww∗=0(16)
假定S w S_wSw是非奇异的(样本数大于维数时),可以得到:
S w − 1 S b w ∗ = λ w ∗ (17) S_w^{-1}S_bw^{*}=\lambda w^{*} \tag {17}Sw−1Sbw∗=λw∗(17)
其中,w ∗ w^{*}w∗是矩阵S w − 1 S b S_w^{-1}S_bSw−1Sb的特征向量,把S b S_bSb代入变成:
λ w ∗ = S w − 1 ( m 1 − m 2 ) ( m 1 − m 2 ) T w ∗ (18) \lambda w^{*}=S_w^{-1}(m_1-m_2)(m_1-m_2)^Tw^{*} \tag {18}λw∗=Sw−1(m1−m2)(m1−m2)Tw∗(18)
主要到,( m 1 − m 2 ) T w ∗ (m_1-m_2)^T w^{*}(m1−m2)Tw∗是标量,不影响w ∗ w^{*}w∗的方向,因此得到w ∗ w^{*}w∗的方向是S w − 1 ( m 1 − m 2 ) S_w^{-1}(m_1-m_2)Sw−1(m1−m2)决定的。
由于我们只关心w ∗ w^{*}w∗的方向,因此可以取:
w ∗ = S w − 1 ( m 1 − m 2 ) (19) w^{*}=S_w^{-1}(m_1-m_2) \tag {19}w∗=Sw−1(m1−m2)(19)
该式即为Fisher准则下的最优投影方向。
图示: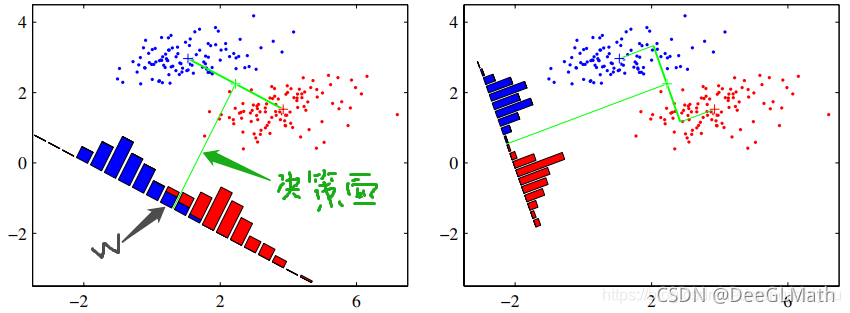
4. 基于鸢尾花卉数据集的LDA代码分析
4.1 属性特征分析
from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np
import math
# 数据准备
iris = datasets.load_iris()
X = iris.data
y = iris.target
names = iris.feature_names # 属性名称
labels = iris.target_names # 类别名称
y_c = np.unique(y) # 离散化数据,去除重复数据
# 用一维直方图来可视化四个属性的特征分布
fig, axes = plt.subplots(2, 2, figsize=(12, 6))
for ax, column in zip(axes.ravel(), range(X.shape[1])):
# 设置图窗大小
min_b = math.floor(np.min(X[:, column]))
max_b = math.ceil(np.max(X[:, column]))
bins = np.linspace(min_b, max_b, 25)
# 绘制直方图
for i, color in zip(y_c, ('blue', 'red', 'green')):
ax.hist(X[y == i, column], color=color, label='%s' % labels[i],
bins=bins, alpha=0.5, )
ylims = ax.get_ylim()
# 绘制注释
l = ax.legend(loc='upper right', fancybox=True, fontsize=8)
l.get_frame().set_alpha(0.5)
ax.set_ylim([0, max(ylims) + 2])
ax.set_xlabel(names[column])
ax.set_title('Iris histogram feature %s' % str(column + 1))
# 隐藏坐标轴
ax.tick_params(axis='both', which='both', bottom=False, top=False, left=False, right=False,
labelbottom=True, labelleft=True)
# 移除其他选项
ax.spines['top'].set_visible(False)
ax.spines["right"].set_visible(False)
ax.spines["bottom"].set_visible(False)
ax.spines["left"].set_visible(False)
axes[0][0].set_ylabel('count')
axes[1][0].set_ylabel('count')
fig.tight_layout()
plt.show()
图示: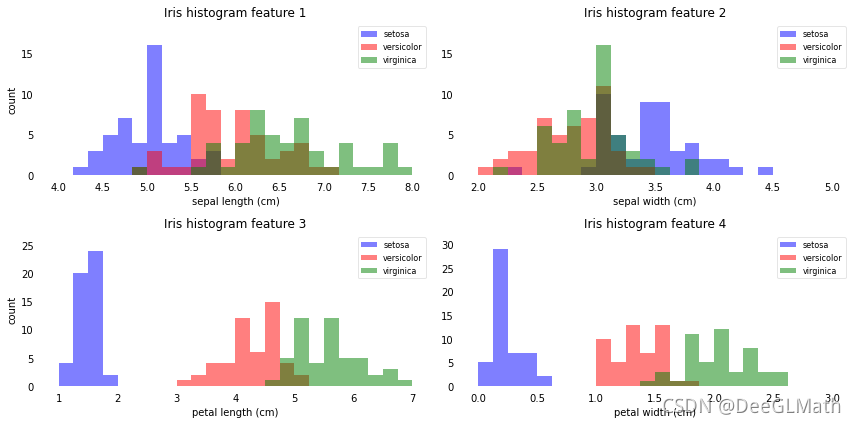
结论:
上述特征图形表示,花瓣的长度和宽度可能更适合分类。
4.2 分步求解相关量
1. 求取d维向量特征值
np.set_printoptions(precision=4)
mean_vector = [] # 类别的平均值
for i in y_c:
mean_vector.append(np.mean(X[y == i], axis=0))
print('均值向量 %s:%s\n' % (i, mean_vector[i]))
结果:
均值向量 0:[5.006 3.428 1.462 0.246]
均值向量 1:[5.936 2.77 4.26 1.326]
均值向量 2:[6.588 2.974 5.552 2.026]
2. 计算类内离散度矩阵
S_W = np.zeros((X.shape[1], X.shape[1]))
for i in y_c:
Xi = X[y == i] - mean_vector[i]
S_W += np.mat(Xi).T * np.mat(Xi)
print('类内离散度矩阵:\n', S_W)
结果:
类内离散度矩阵:
[[38.9562 13.63 24.6246 5.645 ]
[13.63 16.962 8.1208 4.8084]
[24.6246 8.1208 27.2226 6.2718]
[ 5.645 4.8084 6.2718 6.1566]]
3. 计算类间离散度矩阵
S_B = np.zeros((X.shape[1], X.shape[1]))
mu = np.mean(X, axis=0) # 所有样本平均值
for i in y_c:
Ni = len(X[y == i])
S_B += Ni * np.mat(mean_vector[i] - mu).T * np.mat(mean_vector[i] - mu)
print('类间离散度矩阵:\n', S_B)
结果:
类间离散度矩阵:
[[ 63.2121 -19.9527 165.2484 71.2793]
[-19.9527 11.3449 -57.2396 -22.9327]
[165.2484 -57.2396 437.1028 186.774 ]
[ 71.2793 -22.9327 186.774 80.4133]]
4. 计算矩阵S w − 1 S b S_w^{-1}S_bSw−1Sb的特征值与特征向量
eigvals, eigvecs = np.linalg.eig(np.linalg.inv(S_W) * S_B) # 求特征值,特征向量
np.testing.assert_array_almost_equal(np.mat(np.linalg.inv(S_W) * S_B) * np.mat(eigvecs[:, 0].reshape(4, 1)),
eigvals[0] * np.mat(eigvecs[:, 0].reshape(4, 1)), decimal=6, err_msg='',
verbose=True)
5. 为新特征子空间选择线性判别式
eig_pairs = [(np.abs(eigvals[i]), eigvecs[:, i]) for i in range(len(eigvals))]
eig_pairs = sorted(eig_pairs, key=lambda k: k[0], reverse=True)
W = np.hstack((eig_pairs[0][1].reshape(4, 1), eig_pairs[1][1].reshape(4, 1)))
6. 把样本转换到新的子空间
X_trans = X.dot(W)
assert X_trans.shape == (150, 2)
7. 对比sklearn
plt.figure(figsize=(8, 4))
plt.subplot(121)
plt.scatter(X_trans[y == 0, 0], X_trans[y == 0, 1], c='r')
plt.scatter(X_trans[y == 1, 0], X_trans[y == 1, 1], c='g')
plt.scatter(X_trans[y == 2, 0], X_trans[y == 2, 1], c='b')
plt.title('DIY LDA')
plt.xlabel('$LD_1$')
plt.ylabel('$LD_2$')
plt.legend(labels, loc='best', fancybox=True)
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
X_trans2 = LinearDiscriminantAnalysis(n_components=2).fit_transform(X, y)
plt.subplot(122)
plt.scatter(X_trans2[y == 0, 0], X_trans2[y == 0, 1], c='r')
plt.scatter(X_trans2[y == 1, 0], X_trans2[y == 1, 1], c='g')
plt.scatter(X_trans2[y == 2, 0], X_trans2[y == 2, 1], c='b')
plt.title('sklearn LDA')
plt.xlabel('$LD_1$')
plt.ylabel('$LD_2$')
plt.legend(labels, loc='best', fancybox=True)
图示: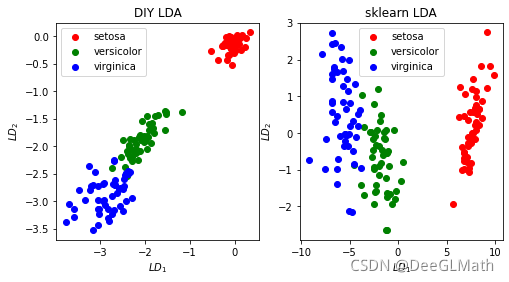
8. 完整代码
from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np
import math
# 数据准备
iris = datasets.load_iris()
X = iris.data
y = iris.target
names = iris.feature_names # 属性名称
labels = iris.target_names # 类别名称
y_c = np.unique(y) # 离散化数据,去除重复数据
# 用一维直方图来可视化四个属性的特征分布
fig, axes = plt.subplots(2, 2, figsize=(12, 6))
for ax, column in zip(axes.ravel(), range(X.shape[1])):
# 设置图窗大小
min_b = math.floor(np.min(X[:, column]))
max_b = math.ceil(np.max(X[:, column]))
bins = np.linspace(min_b, max_b, 25)
# 绘制直方图
for i, color in zip(y_c, ('blue', 'red', 'green')):
ax.hist(X[y == i, column], color=color, label='%s' % labels[i],
bins=bins, alpha=0.5, )
ylims = ax.get_ylim()
# 绘制注释
l = ax.legend(loc='upper right', fancybox=True, fontsize=8)
l.get_frame().set_alpha(0.5)
ax.set_ylim([0, max(ylims) + 2])
ax.set_xlabel(names[column])
ax.set_title('Iris histogram feature %s' % str(column + 1))
# 隐藏坐标轴
ax.tick_params(axis='both', which='both', bottom=False, top=False, left=False, right=False,
labelbottom=True, labelleft=True)
# 移除其他选项
ax.spines['top'].set_visible(False)
ax.spines["right"].set_visible(False)
ax.spines["bottom"].set_visible(False)
ax.spines["left"].set_visible(False)
axes[0][0].set_ylabel('count')
axes[1][0].set_ylabel('count')
fig.tight_layout()
plt.show()
# 求取d维向量特征值
np.set_printoptions(precision=4)
mean_vector = [] # 类别的平均值
for i in y_c:
mean_vector.append(np.mean(X[y == i], axis=0))
print('均值向量 %s:%s\n' % (i, mean_vector[i]))
# 计算类内离散度矩阵
S_W = np.zeros((X.shape[1], X.shape[1]))
for i in y_c:
Xi = X[y == i] - mean_vector[i]
S_W += np.mat(Xi).T * np.mat(Xi)
print('类内离散度矩阵:\n', S_W)
# 计算类间离散度矩阵
S_B = np.zeros((X.shape[1], X.shape[1]))
mu = np.mean(X, axis=0) # 所有样本平均值
for i in y_c:
Ni = len(X[y == i])
S_B += Ni * np.mat(mean_vector[i] - mu).T * np.mat(mean_vector[i] - mu)
print('类间离散度矩阵:\n', S_B)
# 计算矩阵的特征值与特征向量
eigvals, eigvecs = np.linalg.eig(np.linalg.inv(S_W) * S_B) # 求特征值,特征向量
np.testing.assert_array_almost_equal(np.mat(np.linalg.inv(S_W) * S_B) * np.mat(eigvecs[:, 0].reshape(4, 1)),
eigvals[0] * np.mat(eigvecs[:, 0].reshape(4, 1)), decimal=6, err_msg='',
verbose=True)
# 为新特征子空间选择线性判别式
eig_pairs = [(np.abs(eigvals[i]), eigvecs[:, i]) for i in range(len(eigvals))]
eig_pairs = sorted(eig_pairs, key=lambda k: k[0], reverse=True)
W = np.hstack((eig_pairs[0][1].reshape(4, 1), eig_pairs[1][1].reshape(4, 1)))
# 把样本转换到新的子空间
X_trans = X.dot(W)
assert X_trans.shape == (150, 2)
# 对比sklearn
plt.figure(figsize=(8, 4))
plt.subplot(121)
plt.scatter(X_trans[y == 0, 0], X_trans[y == 0, 1], c='r')
plt.scatter(X_trans[y == 1, 0], X_trans[y == 1, 1], c='g')
plt.scatter(X_trans[y == 2, 0], X_trans[y == 2, 1], c='b')
plt.title('DIY LDA')
plt.xlabel('$LD_1$')
plt.ylabel('$LD_2$')
plt.legend(labels, loc='best', fancybox=True)
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
X_trans2 = LinearDiscriminantAnalysis(n_components=2).fit_transform(X, y)
plt.subplot(122)
plt.scatter(X_trans2[y == 0, 0], X_trans2[y == 0, 1], c='r')
plt.scatter(X_trans2[y == 1, 0], X_trans2[y == 1, 1], c='g')
plt.scatter(X_trans2[y == 2, 0], X_trans2[y == 2, 1], c='b')
plt.title('sklearn LDA')
plt.xlabel('$LD_1$')
plt.ylabel('$LD_2$')
plt.legend(labels, loc='best', fancybox=True)