1.二维数组查找问题
思路:矩阵是有序的,从左下角来看,向上数字递减,向右数字递增,因此从左下角(倒数第一个子数组头部开始)开始查找,当要查找数字比左下角数字大时右移,要查找数字比左下角数字小时,上移
在一个二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。
请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
var array = [[0,1,2],[3,4,5],[6,7,8]]
function Find (target,array) {
var i = 0,
j = 0;
var row = array.length
var col = array[0].length
for (i = row-1; i >= 0&& j < col;) {
if (target > array[i][j]) { //从左下角数字开始查询 大于则列+1
j++;
}else if (target < array[i][j]) { // 小于则行-1
i--;
}else{ //等于返回true
return true
}
}
return false // 循环结束,即没有找到,返回false
}
var i = Find(9,array);
console.log(i)2.替换空格
思路:字符串方法拆分,数组方法合成,也可使用正则表达式
请实现一个函数,将一个字符串中的空格替换成“%20”。
例如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy
function replaceScape (str){
return str.split(' ').join('%20');
}
请实现一个函数,将一个字符串中的空格替换成“%20”。
例如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy
function replaceScape (str){
var reg = new RegExp(' ', 'g')
return str.replace(reg, '%20')
}
3.从尾到头打印链表
思路:JS中实现该题目优先考虑数组翻转,将链表值先顺序存入数组,然后将数组逆序即可实现题目要求
输入一个链表,从尾到头打印链表每个节点的值
/*function ListNode(x){
this.val = x;
this.next = null;
}*/
function printListFromTailToHead(head) {
var arr = [];
var temp = head;
while (temp) {
arr.push(temp.val)
temp = temp.next
}
return arr.reverse();
}4.重建二叉树
题目:
给定某二叉树的前序遍历和中序遍历,请重建出该二叉树并返回它的头结点。
例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建出如下图所示。
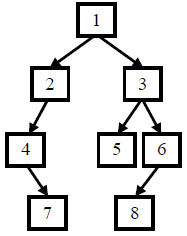
思路:前序遍历时根节点是第一个元素,因此此题中根节点为pre[0]。对于中序遍历,根节点左边的节点位于二叉树的左边,根节点右边的节点位于二叉树的右边,所以找出中序里的根节点进行判断,把数组分为左和右,然后递归出结果
/* function TreeNode(x) {
this.val = x;
this.left = null;
this.right = null;
} */
function reConstructBinaryTree(pre, vin)
{
// write code here
if(!pre.length || !vin.length) {
return null
}
var rootNode = pre[0]
var newTree = new TreeNode(rootNode)
for(var i =0; i < pre.length; i++) {
if (vin[i] === pre[0]) {
newTree.left = reConstructBinaryTree(pre.slice(1,i+1), vin.slice(0,i))
newTree.right = reConstructBinaryTree(pre.slice(i+1), vin.slice(i+1))
}
}
return newTree
}补充知识点:
JavaScript中slice方法可从已有的数组中返回选定的元素,它返回的是一个新的数组,包含从 start 到 end(不包括该元素)的 arrayObject中的元素。请注意,该方法并不会修改数组,而是返回一个子数组。如果想删除数组中的一段元素,应该使用方法 Array.splice(),slice(0,0)和slice(1,1)返回结果都为空。
DLR--前序遍历(根在前,从左往右,一棵树的根永远在左子树前面,左子树又永远在右子树前面 )
LDR--中序遍历(根在中,从左往右,一棵树的左子树永远在根前面,根永远在右子树前面)
LRD--后序遍历(根在后,从左往右,一棵树的左子树永远在右子树前面,右子树永远在根前面)

5.用两个栈实现队列
题目:
用两个栈来实现一个队列,分别完成在队列尾部插入整数(push)和在队列头部删除整数(pop)的功能。 队列中的元素为int类型
思路:首先拿栈1作为入队列,栈2作为出队列
进行删除操作时,当栈2中为空时,就将栈1放入栈2,如栈2不为空,则输出栈2中的数据
!!! 注意:将for循环的条件控制变量直接写成stack1.length,会导致程序运行错误,因为栈1出栈后length会变化,导致栈2中数据存放顺序错误,应先声明 var stack1Len = stack1.length;
var stack1 = [],
stack2 = []
function push(node)
{
// write code here
stack1.push(node)
}
function pop()
{
if(stack2.length === 0) {
if(stack1.length ===0) {
return false
} else {
var stackLth = stack1.length
for (var i = 0; i < stackLth; i++) {
stack2.push(stack1.pop())
}
return stack2.pop()
}
}else {
return stack2.pop()
}
}6.旋转最小数字
题目:
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。
NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
思路:输入一个非递减排序的数组的旋转,说明原始数组的值递增或者有重复,如{1,2,3,6,7} 或者{1,1, 2,2,2,3,6,7}等。那么旋转之后原始数组的最小值必然与某一个元素相邻且不满足递增条件。
function minNumberInRotateArray(rotateArray)
{
// write code here
if (rotateArray.length === 0) {
return 0
}
for(var i = 0; i < rotateArray.length ; i++) {
if (rotateArray[i] > rotateArray[i+1]) {
return rotateArray[i+1]
}
}
return rotateArray[0]
}7.斐波那契数列
题目:
大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0,第1项是1)
n≤39
思路:由于斐波纳挈数列是以兔子的繁殖引入的,因此也叫“兔子数列”。它指的是这样一个数列:0,1,1,2,3,5,8,13……从这组数可以很明显看出这样一个规律:从第三个数开始,后边一个数一定是在其之前两个数的和。在数学上,斐波纳挈数列可以以这样的公式表示:F(0) = 0;F(1) = 1 ;F(n) = F(n-1) + F(n-2),(n>=2)。本题目在求解的时候尽可能避免使用递归,因为递归空间复杂度呈指数级增长。
function Fibonacci(n)
{
// write code here
if(n <=1) {
return n
}else {
let first = 0 ,second = 1, third = 1
for (var i = 2; i <= n; i++) {
third = first + second
first = second
second = third
}
return third
}
}8.跳台阶
题目:
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)
思路:
比较倾向于找规律的解法,f(1) = 1, f(2) = 2, f(3) = 3, f(4) = 5, 可以总结出f(n) = f(n-1) + f(n-2)的规律,但是为什么会出现这样的规律呢?假设现在6个台阶,我们可以从第5跳一步到6,这样的话有多少种方案跳到5就有多少种方案跳到6,另外我们也可以从4跳两步跳到6,跳到4有多少种方案的话,就有多少种方案跳到6,其他的不能从3跳到6什么的啦,所以最后就是f(6) = f(5) + f(4);这样子也很好理解变态跳台阶的问题了
function jumpFloor(number)
{
// write code here
if(number == 1) {
return 1
}else if (number == 2) {
return 2
} else {
var first = 1
var second = 2
var third = 0
for (var i = 3; i <= number; i++) {
third = first + second
first = second
second = third
}
return third
}
}9.变态跳台阶
题目:
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶(n为正整数)总共有多少种跳法。
思路:
因为n级台阶,第一步有n种跳法:跳1级、跳2级、到跳n级
跳1级,剩下n-1级,则剩下跳法是f(n-1)
跳2级,剩下n-2级,则剩下跳法是f(n-2)
所以f(n)=f(n-1)+f(n-2)+…+f(1)
因为f(n-1)=f(n-2)+f(n-3)+…+f(1)
所以f(n)=2*f(n-1)
function jumpFloorII(number)
{
// write code here
if(number <= 1) {
return number
} else {
return 2 * jumpFloorII(number-1)
}
}10.矩形覆盖
题目:
我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形,从同一个方向看总共有多少种不同的方法?

思路:
那就对n 从小到大,一步步分析:

n=1时,显然只有一种方法

n=2时,如图有2种方法

n=3,如图有3中方法

n=4,如图有4种方法。
如果到这里,还没有发现规律怎么办呢?
那我们就再分析以下,从n=3到n=4,怎么来的呢?
这里有2种情况:
- 直接在n=3的情况下,再后面中添加一个竖着的。这个很显然成立,有3种情况
- 然后横着的显然能添加到n-2的情况上,也就是在n=2后面,添加2个横着的。有2种情况
通过以上分析,发现刚好和图中的个数一样。
所以总结:f [n]表示2*n大矩阵 的方法数。
可以得出:f[n] = f[n-1] + f[n-2],初始条件f[1] = 1, f[2] =2
递推方法代码实现:
function rectCover(number)
{
// write code here
if (number==0 || number==1 || number==2) {
return number
}else {
var a = 1, b = 2,c = 0
for (var i = 3; i <= number; i++) {
c = a + b
a = b
b = c
}
return c
}
}