在封闭的多边形中,需要判断一个点在不在图形中
先在点处画一条竖直的线穿过图形
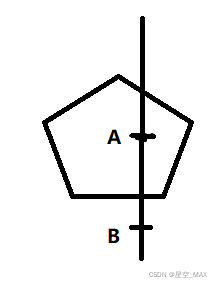
这时候记下A上下两边焦点的个数分别为1,为单数
但是B上下两边焦点的个数分别为0和2,为双数
那么找一个有凹面的多边形呢
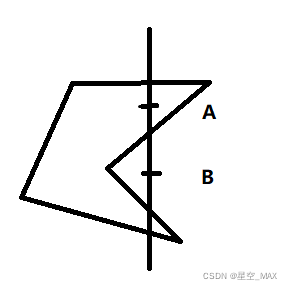
发现也一样
那么就用这个方法来实现,点是否在封闭图形中的判定(cocos2d实现方式)
bool PointInRegion(cocos2d::CCPoint pt,vector<cocos2d>::plist)
{
int Cross=0;
//依次判定每一条边的情况
for(int i=0;i<plist.size(),i++)
{
cocos2d:CCPoint p1;
cocos2d:CCPoint p2;
p1=plist[i];
p2=plist[(i+1)%plist.size()];
//看点的x坐标是不是在两点的x坐标之中
if(pt.x=p2.x)
contine;
if(pt.x<min(p1.x,p2.x))
contine;
if(pt.x>min(p1.x,p2.x))
contine;
//一条垂直线穿过图形,看交点的y坐标
double y = (double)(pt.x - p1.x) * (double)(p2.y - p1.y) / (double)(p2.x - p1.x) + p1.y;
//统计在一边的交点的数量
if(y>pt.y)
nCross++;
}
//当一边的数量为偶数时候点在图形外
if(nCross%2==0)
return false;
//当一边的数量为奇数时候点在图形内
else
return true;
}原理图如下:
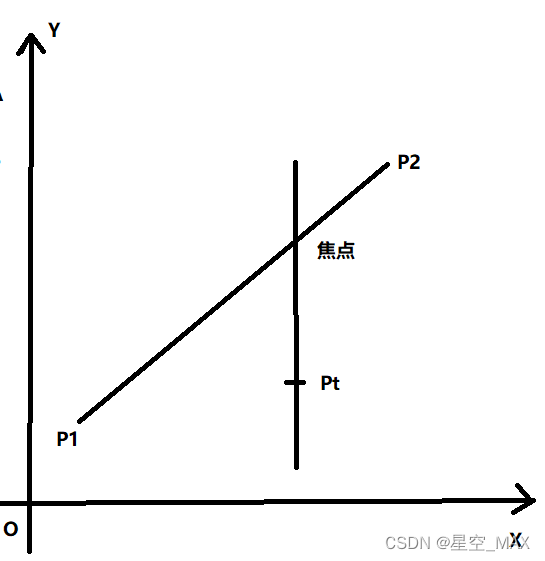
版权声明:本文为qq_36653924原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。