基本问题：
给出n值，求其对应的三次方根
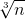的值(该问题可以扩展到多次方根
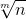的值)
解决思路：
该问题的解决思路可以有两个：
1)类比于在一堆数列里找某一个符合条件的值x，条件为：
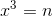，可想而知，最常用的搜索方法为二分法。
其基本思路为：假设n=7
step1: 7/2=3.5;
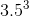=42.875>7;
step2: 3.5/2= 1.75;
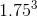=5.359<7;
step3: (1.75+3.5)/2=2.625;
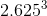=18.088>7;
step4: (1.75+2.625)/2=2.1875;
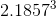=10.47>7
.....
stepn: 通过二分法，不断逼近
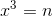，达到最终解。
通过low,high,middle 三个变量进行控制。python代码如下：
# 通过二分法求n的三次方根的值
def cube_root(n):
if(n<0):
temp=-n
else: temp=n
precision=0.0000001
low=0
high= temp/2
while(abs(high*high*high-temp)>precision):
if(high*high*high>temp):
high=high-(high-low)/2
elif(high*high*high
运行结果为：
....... (未完还有)
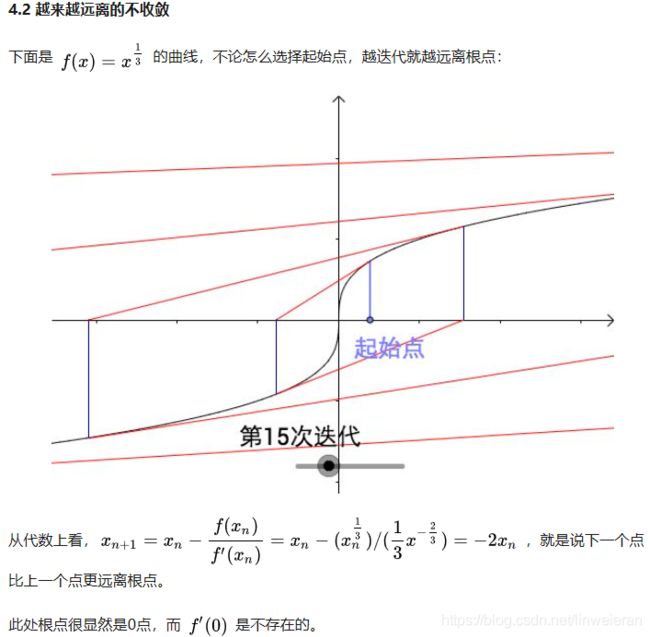
2)使用牛顿迭代进行推导。
牛顿迭代求解这些问题是非常快的，牛顿迭代法顾名思义当然是迭代法的一种，所谓迭代法顾名思义就是重复地进行某种运算。进行到何时为止全凭个人好恶，但是理想情况下应该是计算的次数越多离真正的解就越近 [1]。
但最近看一篇知乎文章里面说，文章链接在参考文献 [2] 中。ps.该文章对牛顿迭代讲解非常清楚，并且有图解释。
特注明：在此引用的知乎内容，无恶意，若作者不希望被引用，联系我则删
参考文献：
[1] 如何通俗易懂地讲解牛顿迭代法求开方？数值分析？ - 鍵山小鞠的回答 - 知乎
https://www.zhihu.com/question/20690553/answer/564405611
[2] 如何通俗易懂地讲解牛顿迭代法求开方？数值分析？ - 马同学的回答 - 知乎
https://www.zhihu.com/question/20690553/answer/146104283