参考资料

高翔slam14讲

1. 李群李代数基础

上一讲,我们介绍了旋转矩阵和变换矩阵的定义。当时,我们说三维旋转矩阵构成了特殊正交群$SO(3)$,而变换矩阵构成了特殊欧氏群$SE(3)$: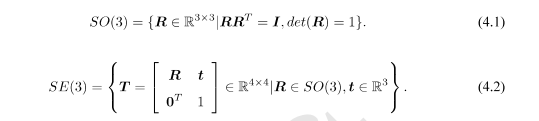

旋转矩阵也好,变换矩阵也好,它们对加法是不封闭的。换句话说,对于任意两个旋转矩阵$R_1,R_2$，它们按照矩阵加法的定义，和不再是一个旋转矩阵：
对于变换矩阵亦是如此。我们发现,这两种矩阵并没有良好定义的加法,相对的,它们只有一种较好的运算:乘法。$SO(3)$和$SE(3)$关于乘法是封闭的:

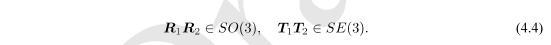
我们知道乘法对应着旋转或变换的复合 一两个旋转矩阵相乘表示做了两次旋转。对于这种只有一个运算的集合,我们把它叫做群。

1.1 群

群(Group)是一种集合加上一种运算的代数结构。我们把集合记作A，运算记作$\cdot$，那么群可以记作$G=(A，\cdot )$。群要求这个运算满足以下几个条件：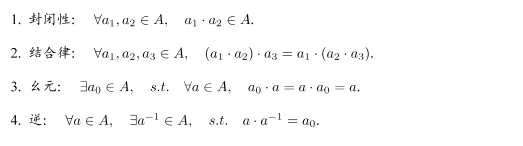

可以记作“封结幺逆”。我们可以验证,旋转矩阵集合和矩阵乘法构成群,同样变换矩阵和矩阵乘法也构成群(因此才能称它们为旋转矩阵群和变换矩阵群)。其他常见的群包括整数的加法$(\mathbb{Z},+)$,去掉0后的有理数的乘法(幺元为1)$(\mathbb{Q}-0,\cdot )$等等。矩阵中常见的群有:

特殊欧氏群SE(n) 也就是前面提到的n维欧氏变换,如SE(2)和SE(3)。群结构保证了在群上的运算具有良好的性质,而群论则是研究群的各种结构和性质的理论。

1.1.1 李群

李群是指具有连续(光滑)性质的群。像整数群$\mathbb{Z}$那样离散的群没有连续性质,所以不是李群。而$SO(n)$和$SE(n)$,它们在实数空间上是连续的。我们能够直观地想象一个刚体能够连续地在空间中运动,所以它们都是李群。

每个李群都有对应的李代数。

1.2 李代数

考虑任意旋转矩阵R,我们知道它满足: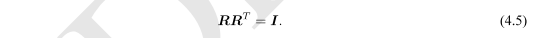

现在,我们说,R是某个相机的旋转,它会随时间连续地变化,即为时间的函数: R(t)。由于它仍是旋转矩阵,有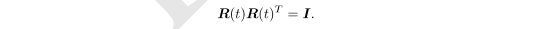

在等式两边对时间求导,得到: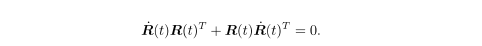


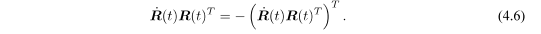
可以看出$\dot{R}(t)R(t{)}^T$是一个反对称矩阵。

叉积中引入了KaTeX parse error: Expected group after '^' at position 1: ^̲符号,将一个向量变成了反对称矩阵。同理,对于任意反对称矩阵,我们亦能找到一个与之对应的向量。把这个运算用符号v表示: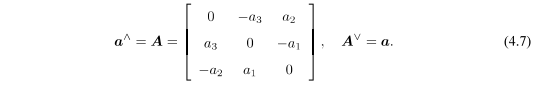

于是,由于$\dot{R}(t)R(t{)}^T$是一个反对称矩阵,我们可以找到一个三维向量$\varphi (t)\in {\mathbb{R}}^3$与之对应。于是有: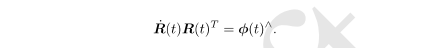

等式两边右乘$R(t)$,由于R为正交阵,有:

1.2.1 李代数的定义

每个李群都有与之对应的李代数。李代数描述了李群的局部性质。通用的李代数的定义如下:

其中二元运算被称为李括号。从表面上来看,李代数所需要的性质还是挺多的。相比于群中的较为简单的二元运算,李括号表达了两个元素的差异。它不要求结合律,而要求元素和自己做李括号之后为零的性质。作为例子,三维向量${\mathbb{R}}^3$上定义的叉积$\times$是一种李括号,因此$g=({\mathbb{R}}^3,\mathbb{R},\times )$构成了一个李代数。

1.2.2 李代数so(3)

1.2.3 李代数se(3)

未完待续···