又到了“最简单”的数论了，
好开心啊~(｡◕ˇ∀ˇ◕)

简单数论

数论函数/算术函数

定义

指在正整数集上的实值或复值函数。
一般地，也可以把其看做是某一整数集上定义的函数，如：$$d(n)=\sum _{d|n}1$$以正整数为定义域的函数 $f(n)$ ，例如 数列 $\{\alpha n\}$ 、 $n!$ 、幂 $n\lambda$ 等都是数论函数。

内容

将 $n$ 质因子分解为 $n=p_1^{l_1}\dots p_s^{l_s}$ 。

① 莫比乌斯函数 $\mu (n)$$$\mu (n)=\{\begin{array}{ll}1& (n=1)\\ (-1{)}^s& (l_1=\cdots =l_s=1)\\ 0& (有某个l_j>1,1⩽j⩽s)\end{array}$$易知，$$\sum _{d|n}\mu (d)=\Delta (n)=\{\begin{array}{ll}1& (若n=1)\\ 0& (若n>1)\end{array}$$
② 欧拉函数 $\phi (n)$ ，易证：$$\phi (mn)=\frac{d\phi (m)\phi (n)}{\phi (d)}$$其中 $(m,n)=d$

③ 除数函数

当 $u!=0$ 时，有$$\mathcal{L}\{f(t)\}=F(s)={\int }_0^{\infty }f(t)e^{-st}\mathrm{d}t$$当 $u=0$ 时，$$f(t)={\mathcal{L}}^{-1}\{F(s)\}=\frac{1}{2\pi j}{\int }_{{\sigma }_0-j\infty }^{{\sigma }_0+j\infty }F(s)e^{st}\mathrm{d}s$$$\sigma 1(n)=\sigma (n)$ ，正整数 $n$ 满足 $\sigma (n)=2n$ 时， $n$ 就叫做完全数。

积性函数

定义

1、积性函数：对于任意互质的整数 $a$ 和 $b$ 有性质 $f(ab)=f(a)f(b)$ 的数论函数。
2、完全积性函数：对于任意整数 $a$ 和 $b$ 有性质 $f(ab)=f(a)f(b)$ 的数论函数。

举例

积性函数：

• $\phi (n)$ — 欧拉函数
• $\mu (n)$ — 莫比乌斯函数，关于非平方数的质因子数目
• $gcd(n,k)$ — 最大公因子，当 $k$ 固定的情况
• $d(n)$ — $n$ 的正因子数目
• $\sigma (n)$ — $n$ 的所有正因子之和
• $\sigma k(n)$ — 因子函数， $n$ 的所有正因子的 $k$ 次幂之和，当中 $k$ 可为任何复数
• $1(n)$ — 不变的函数，定义为 $1(n)=1$（完全积性）
• $ld(n)$ — 单位函数，定义为 $ld(n)=n$（完全积性）
• $ldk(n)$ — 幂函数，对于任何复数、实数 $k$ ，定义为 $ldk(n)=n^k$（完全积性）
• $\epsilon (n)$ — 定义为：若 $n=1,ϵ(n)=1$ ；若 $n>1,\epsilon (n)=0$ 。因此又被称为 “对于狄利克雷卷积的乘法单位” （完全积性）
• $\lambda (n)$ — 刘维尔函数，关于能整除 $n$ 的质因子数目
• $\gamma (n)$ — 定义为 $\gamma (n)=(-1{)}^{\omega (n)}$
• $\omega (n)$ — 加性函数，是不同的能整除 $n$ 的质数的数目
  另外，所有 狄利克雷特征 均是完全积性的
  $\mathcal{T}ips:$有些看不懂没有关系，就当了解一下了。

非积性函数

• $\Lambda (n)$ — 冯·曼戈尔特函数，定义为：当 $n$ 是质数 $p$ 的整数幂， $\Lambda (n)=\ln (p)$ ，否则 $\Lambda (n)=0$
• $\pi (n)$ — 定义为不大于正整数 $n$ 的质数的数目
• $P(n)$ — 一个整数能表示成正整数之和的方法的数目

性质

性质一

根据算数基本定理，若将 $n$ 表示成质因子分解式$$n=p_1^{a_1}{p}_2^{a_2}\cdot \cdot \cdot p_n^{a_n}$$则有$$f(n)=f(p_1^{a_1})f(p_2^{a_2})\cdot \cdot \cdot f(p_n^{a_n})$$

性质二

若 $f$ 为积性函数且有$$f(p^n)=f^n(p)$$则 $f$ 为完全积性函数

狄利克雷卷积

定义

设 $f(n)$ 、 $g(n)$ 是两个数论函数，它们的 $Dirichlet(狄利克雷)$ 卷积也是一个数论函数，其定义为：$$h(n)=\sum _{d|n,d>0}f(d)g\left(\frac{n}{d}\right)$$一般简记为 $h(n)=f(n)\ast g(n)$ 。

函数 $f(n)$ 与 $g(n)$ 的狄利克雷卷积也可以表示为$$h(n)=\sum _{ab=n,a,b>0}f(a)g(b)$$

性质

1、满足结合律。设 $f,g,h$ 为任意三个数论函数，则 $(f\ast g)\ast h=f\ast (g\ast h)$ 。
2、满足交换律。设 $f,g$ 为任意二个数论函数，则 $f\ast g=g\ast f$ 。
3、对于所有数论函数 $f(n)$ ，均有 $f(n)\ast l(n)=l(n)\ast f(n)=f(n)$ ，故 $l(n)$ 在狄利克雷卷积中有单位元的作用，简称 $l(n)$ 为单位数论函数 ,或称 $l(n)$ 为卷积单位元。
4、若 $f(n),g(n)$ 均为积性函数，则 $f\ast g$ 亦为积性函数；反之，若 $g(n)$ 与 $(f\ast g)(n)$ 都是积性函数，则 $f(n)$ 亦为积性函数。特别地，当 $F=f\ast \mu$ 为积性函数时， $f(n)$ 亦为积性函数。
5、若 $g(n)$ 是完全积性函数，且 $h=f\ast g$ ，那么 $f=h\ast \mu g$ ，即若$$h(n)=\sum _{d|n}f(d)g\left(\frac{n}{d}\right)$$则$$f(n)=\sum _{d|n}h(d)\mu \left(\frac{n}{d}\right)g\left(\frac{n}{d}\right)$$

常用的狄利克雷乘积

1、 $\mu \ast U=I$ ，即$$\sum _{d|n}\mu (d)=\{\begin{array}{ll}1& (n=1)\\ 0& (n>1)\end{array}$$2、 $\varphi \ast U=N$ ，其中 $N(n)=n$ ，即$$\sum _{d|n}\varphi (d)=n$$3、 $\mu \ast N=\varphi$ ，其中 $N(n)=n$ ，即$$\sum _{d|n}\mu (d)\frac{n}{d}=\sum _{d|n}d\mu \left(\frac{n}{d}\right)=\varphi (n)$$4、$$\Lambda (n)\ast U=Inn$$5、$$(Inn)\ast \mu (n)=\Lambda (n)$$$\mathcal{T}ips:$ $4、5$ 看不懂没有关系，权当了解一下啦~

莫比乌斯函数

定义

$M\ddot{o}bius$ 函数是指以下函数：$$\mu (n)={\delta }_{\omega (n)\Omega (n)}\lambda (n)$$其中 $\lambda (n)$ 是刘维尔函数。不懂不要紧，反正我也没懂

莫比乌斯函数不仅仅是数论函数，还是积性函数（即 $\mu (a\cdot b)=\mu (a)\cdot \mu (b)$ ，其中 $gcd(a,b)=1$ ）。

当 $n!=1$ 时， $n$ 的所有因子的莫比乌斯函数值之和为 $0$ 。
特别地，当 $n=1$ 时，上述结果为 $1$ 。
即：$$\sum _{d|n}\mu (d)=\{\begin{array}{ll}1& \text{if n=1}\\ 0& \text{if n!=1}\end{array}$$如果你很懵逼，不要怕，接下来我们来一起看一下莫比乌斯函数完整定义的通俗表达：
1、莫比乌斯函数 $\mu (n)$ 的定义域是 $N^{\ast }$ 。( 即：$n\in N^{\ast }$ )
2、 $\mu (1)=1$
3、当 $n$ 存在平方因子时， $\mu (n)=1$
4、当 $n$ 是质数或奇数个不同质数之积时， $\mu (n)=-1$
5、当 $n$ 是偶数个不同质数之积时， $\mu (n)=1$
$\mathcal{T}ips:$上述不同质数之积的质数的指数都是一次的！

总结起来就是：$$\mu (n)=\{\begin{array}{ll}1& n=1\\ (-1{)}^k& n={\prod }_{i=1}^k{p}_i(p为不同质数，且次数都为1)\\ 0& 其余情况\end{array}$$这样，我们就可以绘制出前 $50$ 个莫比乌斯函数值的图像：盗个图

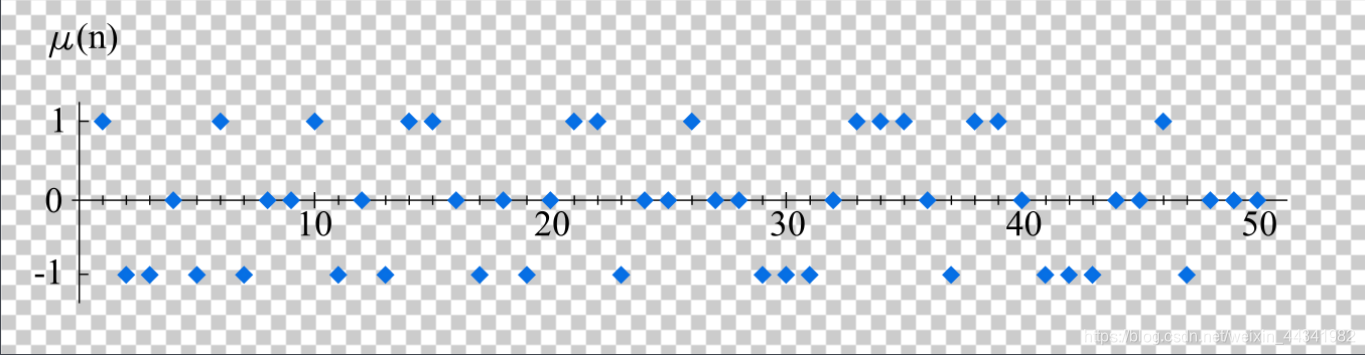
拓展

梅滕斯函数

就是莫比乌斯的求和函数，即$$M(n)=\sum _{i=1}^n\mu (i)$$

莫比乌斯反演

例题导入

先来看一个求和函数：$$F(n)=\sum _{d|n}f(d)$$我们需要找到 $f(n)$ 和 $F(n)$ 之间的关系。按照和函数的定义，我们可以列举前几个看看：$$\begin{array}{rl}& F(1)=f(1)\\ & F(2)=f(1)+f(2)\\ & F(3)=f(1)+f(3)\\ & F(4)=f(1)+f(2)+f(4)\\ & F(5)=f(1)+f(5)\\ & F(6)=f(1)+f(2)+f(3)+f(6)\\ & F(7)=f(1)+f(7)\\ & F(8)=f(1)+f(2)+f(4)+f(8)\end{array}$$所以，$$\begin{array}{rl}& f(1)=F(1)\\ & f(2)=F(2)-f(1)=F(2)-F(1)\\ & f(3)=F(3)-F(1)\\ & f(4)=F(4)-f(2)-f(1)=F(4)-F(2)\\ & f(5)=F(5)-F(1)\\ & f(6)=F(6)-F(3)-F(2)+F(1)\\ & f(7)=F(7)-F(1)\\ & f(8)=F(8)-F(4)\end{array}$$通过对上面这么多式子的 “观察” 可以发现，若 $n=p^2$ ( $p$ 为质数)，那么$$\{\begin{array}{llccccccccc}F(p)=f(1)+f(p)& \cdot \cdot \cdot \cdot \cdot \cdot \cdot ①& & & & & & & & & \\ F(n)=f(1)+f(p)+f(p^2)& \cdot \cdot \cdot \cdot \cdot \cdot \cdot ②& & & & & & & & & \end{array}$$由①②两式可以得到$$f(n)=F(p^2)-F(p)$$如果我们要让函数满足上式，首先我们可以知道 $\mu (p^2)=0$ (因为 $p^2$ 分解质因数必然会有至少两个相同的质数)，于是我们做出如下猜测：$$f(n)=\sum _{d|n}\mu (d)F(\frac{n}{d})$$

定理

设 $f(n)$ 和 $g(n)$ 是定义在正整数集合上的两个函数，定义如下。
若函数 $f(n)$ 满足：$$f(n)=\sum _{d|n}g(d)=\sum _{d|n}g\left(\frac{n}{d}\right)$$则有，$$g(n)=\sum _{d|n}\mu (d)f\left(\frac{n}{d}\right)=\sum _{d|n}\mu \left(\frac{n}{d}\right)f(d)$$

证明

先证充分性：$$\begin{array}{rl}& f(n)=\sum _{d|n}g(d)=\sum _{d|n}g\left(\frac{n}{d}\right)\cdot \cdot \cdot \cdot \cdot \cdot \cdot ①\\ & 由①可得，\\ & \sum _{d|n}\mu (d)f\left(\frac{n}{d}\right)=\sum _{d|n}\mu (d)\sum _{d_1|\frac{n}{d}}g(d_1)=\sum _{d|n}\sum _{d_1|\frac{n}{d}}\mu (d)g(d_1)\\ & \sum _{d|n}\sum _{d_1|\frac{n}{d}}\mu (d)g(d_1)=\sum _{d_1|n}\sum _{d|\frac{n}{d_1}}\mu (d)g(d_1)\end{array}$$上面这一步其实很好理解， $d$ 是 $n$ 的约数，那么 $\frac{n}{d}$ 自然也是 $n$ 的约数 $\iff n$ ，而 $d_1$ 又是 $\frac{n}{d}$ 的约数，所以 $d_1$ 也是 $n$ 的约数并且 $d_1\iff d$ ，得到了上式。

继续将上式化简，$$\sum _{d_1|n}\sum _{d|\frac{n}{d_1}}\mu (d)g(d_1)=\sum _{d_1|n}g(d_1)\sum _{d|\frac{n}{d_1}}\mu (d)$$考虑到，$$\sum _{d|\frac{n}{d_1}}\mu (d)=\{\begin{array}{ll}1& d_1=n\\ 0& d_1<n\end{array}$$这个公式是由莫比乌斯函数定义中第一个大括号扩起来的公式转化而来，所以我们可以推出：$$\sum _{d_1|n}g(d_1)\sum _{d|\frac{n}{d_1}}\mu (d)=g(n)$$因此，$$g(n)=\sum _{d|n}\mu (d)f\left(\frac{n}{d}\right)=\sum _{d|n}\mu \left(\frac{n}{d}\right)f(d)$$

再来证明必要性：$$\begin{array}{rl}& g(n)=\sum _{d|n}\mu (d)f\left(\frac{n}{d}\right)=\sum _{d|n}\mu \left(\frac{n}{d}\right)f(d)\cdot \cdot \cdot \cdot \cdot \cdot \cdot ①\\ & 由①可得,\end{array}$$$$\begin{array}{rl}\sum _{d|n}g(d)& =\sum _{d|n}g\left(\frac{n}{d}\right)\\ & =\sum _{d|n}\sum _{d_1|\frac{n}{d}}\mu \left(\frac{n}{d{d}_1}\right)f(d_1)\\ & =\sum _{d_1|n}\sum _{d|\frac{n}{d_1}}\mu \left(\frac{n}{d{d}_1}\right)f(d_1)\\ & =\sum _{d_1|n}f(d_1)\sum _{d|\frac{n}{d_1}}\mu \left(\frac{n}{d{d}_1}\right)\end{array}$$考虑到，$$\sum _{d|\frac{n}{d_1}}\mu \left(\frac{n}{d{d}_1}\right)=\sum _{d|\frac{n}{d_1}}\mu (d)=\{\begin{array}{ll}1& d_1=n\\ 0& d_1<n\end{array}$$于是我们可以推出，$$\sum _{d_1|n}f(d_1)\sum _{d|\frac{n}{d_1}}\mu \left(\frac{n}{d{d}_1}\right)=f(n)$$因此，$$f(n)=\sum _{d|n}g(d)=\sum _{d|n}g\left(\frac{n}{d}\right)$$

综上可知，$$\begin{array}{rl}& f(n)=\sum _{d|n}g(d)=\sum _{d|n}g\left(\frac{n}{d}\right)\\ & g(n)=\sum _{d|n}\mu (d)f\left(\frac{n}{d}\right)=\sum _{d|n}\mu \left(\frac{n}{d}\right)f(d)\end{array}$$

性质

1、公式： $f(n)={\sum }_{d|n}\mu (d)F\left(\frac{n}{d}\right)$
2、 $\mu (n)$ 是积性函数
3、设 $f$ 是算术函数，它的和函数 $F(n)={\sum }_{d|n}f(d)$ 是积性函数，那么 $f$ 也是积性函数