写在前面的话：
线性代数之所以让人十分头疼，关键点在于线性代数的概念之多，定理之多，前后联系十分紧密。我们很容易学着忘着。为此，小季开始写有关线代复习的文章。将知识点总结起来串联起来，帮助大家更好的复习！
如果帮助到了你，点个赞点个关注哦！感谢支持！
前期回顾：
小季不是咸鱼：一起复习线代！线性代数期末复习之线性方程组~zhuanlan.zhihu.com
1.矩阵A与B相等是指两个矩阵的对应位置上的元素都一一相等
2.矩阵的加法和数乘运算统称为矩阵的线性运算
3.矩阵的加法和数乘满足交换律，结合律和分配律
4.只有矩阵A的列数等于矩阵B的行数，A与B的乘积AB才有意义
5.A与B的乘积AB继承了左边矩阵A的行数，右边矩阵B的列数
6.如果A=0或者B=0，那么AB=0,反之不一定成立
7.如果 A的第i行为零行，那么AB的第i行为零行，如果B的第j列为零列，那么AB的第j列为零列。
8.AB的非零行个数小于等于A的非零行个数，AB的非零列个数小于等于B的非零列个数
9.矩阵的乘法满足结合律和分配律，不满足交换律.A与B可以相乘，B与A不一定可以相乘.
10.矩阵乘法也不满足消去律，即AB=AC，且
11.对于任意的m×n矩阵A，都有
12.关于矩阵乘方的性质
- 如果A为方阵，s,t为非负整数，那么
- 如果A,B为同阶方阵，m为正整数。如果AB可以交换，即AB=BA,那么前提很重要）
（一定注意这个
13.设
14.矩阵转置的性质
- 如果
15.矩阵A的初等列变换
- 互换A的第i列与第j列
- A的第i列乘以非零常数h
- A的第i列的k倍加到第j列上
16.矩阵的初等行变换和初等列变换统称为矩阵的初等变换
17.如果矩阵A可以经过有限次初等变换化为矩阵B，那么称A与B是等价的，记为
18.对n阶单位矩阵
19.关于初等矩阵的转置
20.设A为m×n矩阵.如果对A作一次初等行变换得到的矩阵为B，相同的初等行变换作用到m阶单位矩阵上得到的初等矩阵为P，那么
21.由20可以推出来一下结论
- 矩阵A与B是行等价的当且仅当存在m阶初等矩阵
- 矩阵A与B是列等价的当且仅当存在n阶初等矩阵
- 矩阵A与B是等价的当且仅当存在n阶初等矩阵
22.如果P为初等矩阵，那么存在同阶初等矩阵Q，使得
23.设P是n阶初等矩阵，那么
24.如果矩阵A与B是行等价的，那么B与A也是行等价的
25.设A,B,C是三个矩阵，如果A与B行等价，那么AC与BC也行等价
证明如下：A与B行等价，则由21可知，存在初等矩阵
两边右乘矩阵C可得
26.如果矩阵A与B是行等价的，那么A与B的非零列个数相等，如果矩阵A与C是列等价的，那么A与B的非零行个数相等
注意行列关系
27.矩阵A的秩不大于A的非零行的个数，也不大于A的非零列的个数
28.如果矩阵A与B是等价的，那么
29.矩阵A的秩与A的转置矩阵
30.
31.设A是n阶矩阵，如果r(A)=n,那么A可以表示为有限个初等矩阵的乘积
32.如果A是可逆矩阵，那么A的逆矩阵是唯一的.
33.可逆矩阵的一些性质，将可逆矩阵
34.初等矩阵是可逆的，并且初等矩阵的逆矩阵仍然是初等矩阵
35.设A是n阶矩阵，那么下列论断彼此等价
- A是可逆矩阵
- A可以表示为有限个n阶初等矩阵的乘积
36.设A,B都是n阶矩阵，如果乘积AB是可逆的，那么A与B都是可逆的
37.如果A是n阶初等矩阵，那么线性方程组
38.设A是m×n矩阵，如果P是m阶可逆矩阵，Q是n阶可逆矩阵，那么
39.一些特殊矩阵
- 分块矩阵，如
- 对称矩阵:
- 对角矩阵：简记为
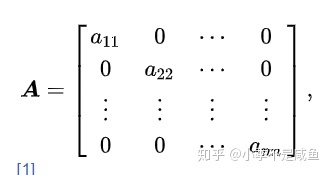
- 准对角矩阵：是一种特殊的分块矩阵
- 上三角矩阵：若A为上三角矩阵，当A可逆时，A的逆矩阵仍然是上三角矩阵
- 下三角矩阵：若A为下三角矩阵，当A可逆时，A的逆矩阵仍然是下三角矩阵
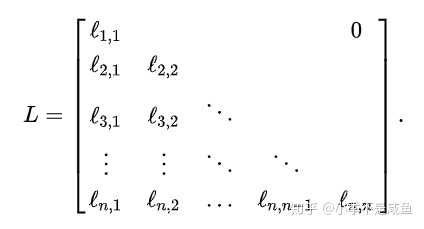
基础题型
1.根据矩阵的运算法则求矩阵（熟练掌握矩阵的乘法）
2.证明某一矩阵为可逆矩阵
3.求可逆矩阵的逆矩阵
4.利用可逆矩阵求方程组的解
5.上述题型与某些特殊矩阵联系
【1】已知矩阵
【2】已知
【3】求平方等于零矩阵的所有 2 阶矩阵
由于该方程组不是线性方程组，故需要分类讨论求解
【4】设
解：计算可得
多加注意这个求乘方的方法
【5】已知矩阵
解：B是 A经过 3 次初等行变换得到的：首先将 A的第 1 行加到第 3 行上， 然后互换矩阵第 1 行与第 2 行，最后互换矩阵的第 2 列和第 3 列，因此令
于是
【6】求下列矩阵的逆矩阵
求一个矩阵的逆矩阵的方法：若A为n阶可逆矩阵
（1）构造n×（2n）矩阵
（2）用初等行变换将
（3）写出
【7】设方阵
一般情况下，在不好进行因式分解时，可以采用待定系数法
【8】求满足以下等式的矩阵
解：
遇到这类题的时候，切记不要用待定系数法设矩阵
【9】设
与逆矩阵相关的证明题中，一定要想办法凑逆矩阵与可逆矩阵的乘积，一般都是在等式两边同时左乘或者又乘
【10】已知
一定要注意在进行矩阵分块的时候，要让分块的小矩阵乘积有意义，即
【11】利用分块矩阵求下列矩阵的逆矩阵
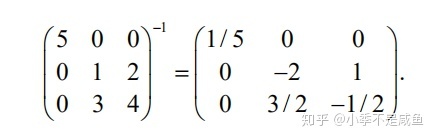
在利用分块矩阵求逆矩阵的时候，注意下面两个公式
尽量凑成这两种形式
【12】证明: 如果 与 都是 n阶对称矩阵, 那么
写在后面的话：
因为篇幅和时间问题，目前更新的线代复习系列依旧以基础知识基础题型为主，感谢大家的谅解
之后 线性代数期末复习系列还会持续更新！！ 希望大家持续关注啦 想要不迷路的话，快快关注小季！
码字不易，能力有限，如有错误，敬请指出
往期回顾
小季不是咸鱼：不定积分大集合——方法篇
小季不是咸鱼：你真的会求导吗？盘点那些复杂、易错、奇怪的求导问题！
小季不是咸鱼：干货驾到，一篇文章带你彻底学会无求小求极限！
小季不是咸鱼：又是干货？用定义证明极限的高阶用法！！
小季不是咸鱼：干货拉满，用定义证明极限的方法汇总
小季不是咸鱼：面对阶乘不会放缩？用泰勒就完事了！