目录
- 传统互信息
- Estimating Mutual Information中的的两种基于最近邻的互信息
- Mutual Information between Discrete and Continuous Data Sets论文中提到的互信息
1. 传统互信息
- 已知变量( X , Y ) (X,Y)(X,Y)的联合概率密度
对于一个N NN维的双变量点对( x i , y i ) , i = 1 , . . . N (x_i, y_i), i = 1, . . . N(xi,yi),i=1,...N,假设其是由联合概率密度为μ ( x , y ) \mu(x,y)μ(x,y)的变量( X , Y ) (X,Y)(X,Y)生成的一组独立同分布的数据,由此我们可以计算得到x , y x,yx,y各自的边缘概率密度,即,μ ( x ) = ∫ μ ( x , y ) d ( x ) \mu(x)=\int\mu(x,y)d(x)μ(x)=∫μ(x,y)d(x),μ ( y ) = ∫ μ ( x , y ) d ( y ) \mu(y)=\int\mu(x,y)d(y)μ(y)=∫μ(x,y)d(y)。由此,我们可以根据下述公式计算得到变量( X , Y ) (X,Y)(X,Y)的互信息I ( X , Y ) I(X,Y)I(X,Y)。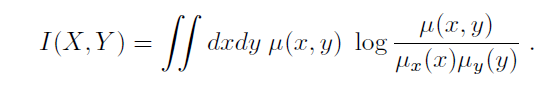
在解决实际问题的时候,我们通常是不知道变量( X , Y ) (X,Y)(X,Y)的联合概率密度的,而且,变量X XX与变量Y YY一般来说是离散的,由此,我们采用分箱(binning)的方法,来计算变量( X , Y ) (X,Y)(X,Y)的互信息。
- 分箱法求解离散变量( X , Y ) (X,Y)(X,Y)的互信息
分箱这个词是我在读论文的时候看到的,我认为可以理解为区间划分,就是将变量X XX与变量Y YY分别进行区间划分。(数学这东西,区间划分就区间划分呗,非要整个什么分箱?)
话不多说,我们直接上公式: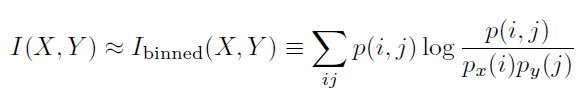
这个算法呢,首先就是将变量X XX与变量Y YY的取值区间进行分箱,统计落入变量X XX的各个箱子内点的数量,同理,统计落入变量Y YY的各个箱子内点的数量,最后对这两组箱子,两两组合,形成二维的箱子,再统计落入这些箱子内点的数量,然后都除以N NN,就得到了对应的概率。
这里我说一下,在机器学习中,我们通常假设样例总共为M MM个,有N NN维特征,我们统计的是每一维度的特征向量与我们的输出Y YY之间的互信息值,互信息越大,说明这个特征与输出结果越相关,简单来说,谁大选谁。因此,数量点(样例)应该是M MM个,这个不要和特征维数混了,这里我用N NN来表示样例点,是遵从论文中的设定……(不想打公式就直说)
好了,回到正文,下面用数学方式来具体描述下如何计算,我们记n x ( i ) n_x(i)nx(i)为落入到变量X XX的第i ii个箱子内点的数量,记n y ( j ) n_y(j)ny(j)为落入到变量Y YY的第j jj个箱子内点的数量,记n ( i , j ) n(i,j)n(i,j)为同时落入到这两个箱子内点的数量,于是,我们有p x ( i ) ≈ p_x(i)\thickapproxpx(i)≈n x ( i ) / N n_x(i)/Nnx(i)/N,p y ( j ) ≈ p_y(j)\thickapproxpy(j)≈n y ( j ) / N n_y(j)/Nny(j)/N,p ( i , j ) ≈ p(i,j)\thickapproxp(i,j)≈n ( i , j ) / N n(i,j)/Nn(i,j)/N。
看到这里,大家也会想到,如何分箱呢?
不同的特征向量对应的量纲不同,所以先对归一化后再对变量X XX分箱我认为是一个好的选择,对于变量Y YY而言,如果是分类问题的话,每个Y YY的取值对应一个箱子即可,而对于回归问题,分箱的方法也可以做,但是在论文:Mutual Information between Discrete and Continuous Data Sets中给出了一种基于K近邻的方法对离散的X XX与连续的Y YY进行计算互信息。
2. Estimating Mutual Information中的两种基于最近邻的互信息
回顾:在分类算法中,最近邻是个非参数方法,每次给予一个需要预测的样本点,我们需要重新计算下距离此点最近的k kk(通常为奇数,投票方便)个已知点,然后取出现频率最高的点对应的标签作为预测样本点的标签。
- 算法一
在k kk最近邻算法中,我们度量距离采用的是的欧式距离,作用于每个特征。
在此论文的第一个算法上,度量距离的方法如下,其选择在X XX方向与Y YY方向的欧式距离最大值作为选择最近邻的标准。这里将( X , Y ) (X,Y)(X,Y)组成的点对记为Z ZZ。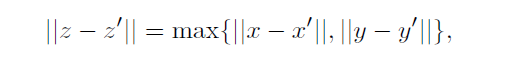
将z i z_izi到它的第k kk个邻居的距离记为ε ( i ) / 2 \varepsilon(i)/2ε(i)/2,这个距离投影到X XX子平面与Y YY子平面的距离分别记为ε x ( i ) / 2 \varepsilon_x(i)/2εx(i)/2,ε y ( i ) / 2 \varepsilon_y(i)/2εy(i)/2,所以根据上面定义的规则,很显然ε ( i ) = m a x { ε x ( i ) , ε y ( i ) } \varepsilon(i)=max\left\{ \varepsilon_x(i), \varepsilon_y(i)\right \}ε(i)=max{εx(i),εy(i)}。
随后,我们对到点x i x_ixi的距离小于ε ( i ) \varepsilon(i)ε(i)的点进行计数,这个数量记为n x ( i ) n_x(i)nx(i);同时,对到点y i y_iyi的距离小于ε ( i ) \varepsilon(i)ε(i)的点进行计数,数量记为n y ( i ) n_y(i)ny(i)。
如下面的图所示,这个是取k kk等于1的情形,可以看到n x ( i ) = 5 n_x(i)=5nx(i)=5 (水平方向小于ε ( i ) \varepsilon(i)ε(i)),n x ( i ) = 3 n_x(i)=3nx(i)=3
随后,根据下面的公式进行计算,可以得到变量X XX与变量Y YY之间的互信息值,这里的⟨ . . . ⟩ \left \langle ...\right \rangle⟨...⟩是指均值的意思,上面的过程只是对N NN个点对中的某个点对z i z_izi进行的统计,我们需要统计所有点对的n x n_xnx与n y n_yny。
符号ψ \psiψ表示的是伽玛函数,其满足迭代规则:ψ ( x + 1 ) = ψ ( x ) + 1 / x \psi(x+1)=\psi(x)+1/xψ(x+1)=ψ(x)+1/x,ψ ( 1 ) = − C \psi(1)=-Cψ(1)=−C,C = 0.5772156... C=0.5772156...C=0.5772156...。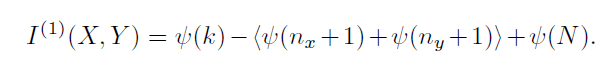
公式定义地非常严谨哈