1、泰勒公式
(1)一元泰勒展开
函数在一个点的邻域内的值可以用函数在该点的值及各阶导数值组成的级数表示出来,设它在x0点存在直到n阶导数,由这些导数构造一个n次多项式如下:
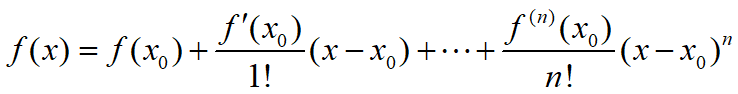
(2)多元泰勒展开
设 y=f(x1, x2, …, xn),则其在(x*1, x*2, x*3, …, x*n )处的泰勒展开式为:

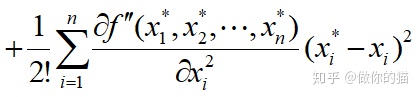

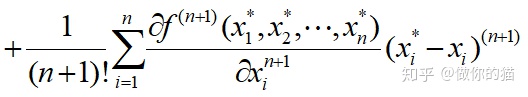
2、一元函数的情况
计算y=f(x)的值,设给定的值x*是近似值,由此计算得到的y也是近似值y*=f(x*),现在研究y*的绝对误差与相对误差。
将x*在x处按照一阶泰勒展开,则会得如下结果:
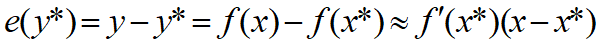
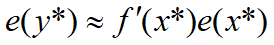
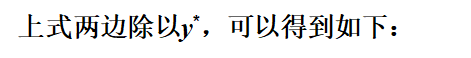
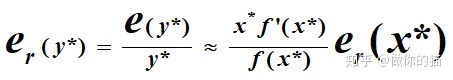
3、多元函数的情况
设x*1, x*2, x*3, …, x*n ,依次是x1, x2, x3, …, xn的近似值,计算 的绝对误差和相对误差。
将 在 x*1, x*2, x*3, …, x*n处进行泰勒展开,最终可以得到y*的一阶绝对误差和相对误差如下:
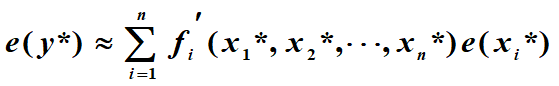
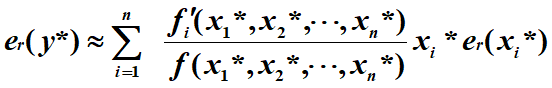
4、加、减、乘、除误差限的计算
两个近似数x*1,x*2,其误差分别为e(x*1)和e(x*2),对它们进行加、减、乘、除运算得到的误差分别为:
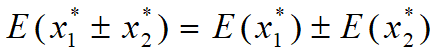
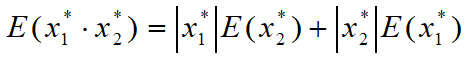
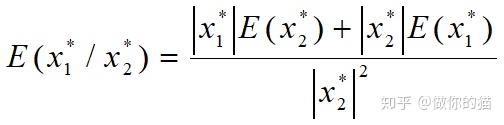
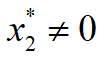
5.误差传播规律
一、尽量避免两个相近的数相减
1、数值计算中,两相近数相减会严重损失有效数字。
如x=532.65,y=532.32都具有5位有效数字,但x-y=0.13有两位有效数字
2、如何避免这种运算发生(改变算法)
(1)当x很大时
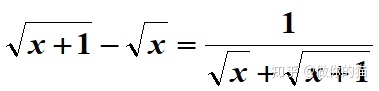
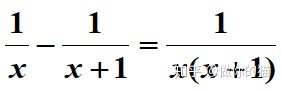
(2)当x1与x2很接近时
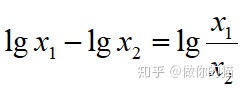
(3)当x接近于0时
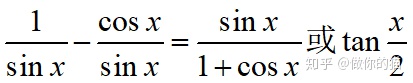
(4)一般情况下,当x*位于x附近时,可以用泰勒级数展开
二、避免大数吃小数的现象
1、若参加运算的数量级相差很大而计算机的位数有限,如不注意运算次序,可能出现大数“吃”小数现象,影响计算结果。
如:当|a|>>|b|时,尽量避免a+b。
三、避免使用绝对值较小的数做除数

四、注意简化计算步骤,减少运算次数
如果能够减少运算次数,即能节省计算机的运行时间,又能减少舍入误差。
五、选择数值稳定性好的算法 (重要,下面例子做实验)
把运算过程中舍入误差不增长的计算公式称为数值稳定的,否则称为不稳定的。