时域分析法
这里写目录标题
引
时域分析法是一种关注于时间域内系统响应的分析方法。根据响应表达式来分析系统的动态性能与稳定性能。
比如,求解知一系统的单位阶跃响应函数h ( t ) = 1 − e − 1 T t h(t)=1-e^{-\frac{1}{T}t}h(t)=1−e−T1t,那么根据该响应函数,可以出判断该系统稳态误差为0,无超调量等。
为了比较系统性能的优劣,我们需要一些比较的基础与标准。比如,我们在什么样的起始条件下,加什么样的输入信号,等等,这些是基础;我们如何根据基础一定的系统输出来比较性能,比如波动大的与波动小的哪个好,这些是标准。
时域分析基础
时域分析的初始条件基础为零初始条件。在零初始条件下,输入典型信号。零初始条件指,系统的输入量在0 + 0^+0+时刻施加,在此之前全为0。这些典型输入信号包括以下几个:
| 信号 | 拉普拉斯变换 | 图像 | 响应函数的拉普拉斯变换 |
|---|---|---|---|
| 单位脉冲信号δ ( t ) \delta(t)δ(t) | 1 11 | 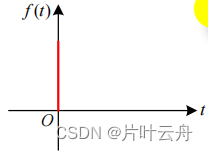 | Φ ( s ) \Phi(s)Φ(s) |
| 单位阶跃信号1 ( t ) 1(t)1(t) | 1 s \frac{1}{s}s1 | 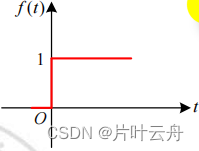 | Φ ( s ) 1 s \Phi(s)\frac{1}{s}Φ(s)s1 |
| 单位斜坡信号t*1(t) | 1 s 2 \frac{1}{s^2}s21 | 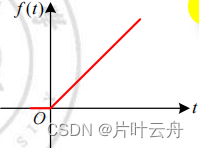 | Φ ( s ) 1 s 2 \Phi(s)\frac{1}{s^2}Φ(s)s21 |
| 单位加速度信号 | 1 s 3 \frac{1}{s^3}s31 | Φ ( s ) 1 s 3 \Phi(s)\frac{1}{s^3}Φ(s)s31 | |
| 正弦信号A s i n ( w t ) ∗ 1 ( t ) Asin(wt)*1(t)Asin(wt)∗1(t) | A w s 2 + w 2 \frac{Aw}{s^2+w^2}s2+w2Aw | 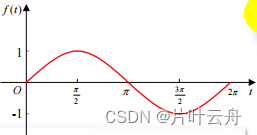 | Φ ( s ) A w s 2 + w 2 \Phi(s)\frac{Aw}{s^2+w^2}Φ(s)s2+w2Aw |
对于上述除正弦信号之外的四种信号,它们之间存在着积分、微分的关系。我们知道s为微分算子,1 s \frac{1}{s}s1为积分算子。所以单位加速度函数求导即为单位斜坡函数,再求导即为单位阶跃函数,再求导即为单位脉冲函数。同理,它们的响应函数也存在这样的关系(前提条件是该系统为线性定常系统)。
时域分析标准
在确立时域分析的基础(零初始条件、典型输入信号)时,我们有许多典型输入信号。而且我们知道它们之间以及它们的响应函数之间存在着积分微分关系,所以我们只要在其中选取一个,就能通过这个关系得到所有的响应函数。
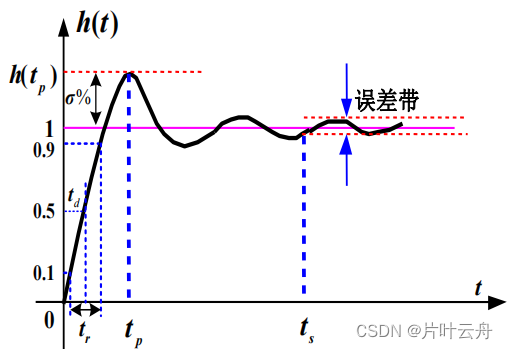
我们选取最易得的单位阶跃信号,作为衡量系统性能好坏时的基准输入,以此确立时域分析性能指标。性能指标有如下几种:
| 指标 | 意义 |
|---|---|
| 延迟时间t d t_dtd | 响应曲线0%到达稳态值50%的时间 |
| 上升时间t r t_rtr | 10%到90%时间(稳态值) |
| 调节时间t s t_sts | 到5%误差带内时间 |
| 峰值时间t p t_ptp | 第一次到达峰值时间 |
| 超调量σ % \sigma\%σ% | 超出稳态值最大偏差除以稳态值 |
| 稳态误差e s s e_{ss}ess | e s s = 1 − h ( ∞ ) e_{ss}=1-h(\infty)ess=1−h(∞) |
一阶系统时域分析
由一阶线性微分方程描述的系统称为一阶系统。
其数学模型为:
T d c ( t ) d t + c ( t ) = r ( t ) T\frac{dc(t)}{dt}+c(t)=r(t)Tdtdc(t)+c(t)=r(t)
拉普拉斯变换得到开环传递函数与闭环传递函数:
G ( s ) = 1 T s G(s)=\frac{1}{Ts}G(s)=Ts1
Φ ( s ) = 1 T s + 1 \Phi(s)=\frac{1}{Ts+1}Φ(s)=Ts+11
单位阶跃响应:
C ( s ) = Φ ( s ) R ( s ) = 1 T s + 1 1 s C(s)=\Phi(s)R(s)=\frac{1}{Ts+1}\frac{1}{s}C(s)=Φ(s)R(s)=Ts+11s1
做拉普拉斯反变换得:
h ( t ) = 1 − e − 1 T t h(t)=1-e^{-\frac{1}{T}t}h(t)=1−e−T1t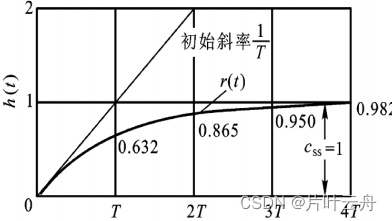
对该响应函数分析:
| 指标 | 值 |
|---|---|
| 延迟时间t d t_dtd | T l n ( 2 ) Tln(2)Tln(2) |
| 上升时间t r t_rtr | 2 T l n ( 3 ) 2Tln(3)2Tln(3) |
| 调节时间t s t_sts | 3 T ( 5 % ) 4 T ( 2 % ) 3T(5\%)4T(2\%)3T(5%)4T(2%) |
| 峰值时间t p t_ptp | 无 |
| 超调量σ % \sigma\%σ% | 无 |
| 稳态误差e s s e_{ss}ess | e s s = 0 e_{ss}=0ess=0 |
二阶系统时域分析
二阶线性定常微分方程描述得系统即为二阶系统。
其数学模型为:
d 2 c ( t ) d t 2 + 2 ζ w n 2 d c ( t ) d t + w n 2 c ( t ) = w n 2 r ( t ) \frac{d^2c(t)}{dt^2}+2\zeta w_n^2\frac{dc(t)}{dt}+w_n^2c(t)=w_n^2r(t)dt2d2c(t)+2ζwn2dtdc(t)+wn2c(t)=wn2r(t)
做Laplace变换得到开环传递函数与闭环传递函数:
G ( s ) = w n 2 s 2 + 2 ζ w n s G(s)=\frac{w_n^2}{s^2+2\zeta w_ns}G(s)=s2+2ζwnswn2
Φ ( s ) = w n 2 s 2 + 2 ζ w n s + w n 2 \Phi(s)=\frac{w_n^2}{s^2+2\zeta w_ns+w_n^2}Φ(s)=s2+2ζwns+wn2wn2
此时不能像一阶系统那样直接求解h(t),需要对其特征方程得特征根进行讨论。
可以根据其微分方程或闭环传递函数直接写出其特征方程:
s 2 + 2 ζ w n s + w n 2 = 0 s^2+2\zeta w_ns+w_n^2=0s2+2ζwns+wn2=0
求出其特征根为:
s 1 , 2 = − ζ w n ± w n ζ 2 − 1 s_{1,2}=-\zeta w_n\pm w_n\sqrt{\zeta^2-1}s1,2=−ζwn±wnζ2−1
可以分为三种情况讨论:
| 情况 | 特征根 | ζ \zetaζ |
|---|---|---|
| 过阻尼 | 两个不同实根 | ζ > 1 \zeta>1ζ>1 |
| 临界阻尼 | 两个相同的实根 | ζ = 1 \zeta=1ζ=1 |
| 欠阻尼与无阻尼 | 两个共轭复根 | 0 ≤ ζ < 1 0\leq \zeta<10≤ζ<1 |
过阻尼情况
过阻尼时,ζ > 1 \zeta>1ζ>1,特征方程有着两个不同的实根。此时,二阶系统的闭环传递函数可以写成:
Φ ( s ) = w n 2 s 2 + 2 ζ w n s + w n 2 = 1 ( T 1 s + 1 ) ( T 2 s + 1 ) 对 应 可 得 : T 1 T 2 = 1 w n 2 , T 1 + T 2 = 2 ζ w n 所 以 : T 1 , 2 = 1 w n ( ζ ± ζ 2 − 1 ) = 1 s 1 , 2 \begin{aligned} \Phi(s)=&\frac{w_n^2}{s^2+2\zeta w_ns+w_n^2}\\ =&\frac{1}{(T_1s+1)(T_2s+1)}\\ 对应可得:\\ &T_1T_2=\frac{1}{w_n^2},T_1+T_2=\frac{2\zeta}{w_n}\\ 所以:\\ T_{1,2}=&\frac{1}{w_n(\zeta \pm\sqrt{\zeta^2-1})}=\frac{1}{s_{1,2}} \end{aligned}Φ(s)==对应可得:所以:T1,2=s2+2ζwns+wn2wn2(T1s+1)(T2s+1)1T1T2=wn21,T1+T2=wn2ζwn(ζ±ζ2−1)1=s1,21
即,过阻尼的二阶系统可以看为两个一阶惯性环节的串联。
此时来求单位阶跃响应函数:
C ( s ) = Φ ( s ) R ( s ) = 1 ( T 1 s + 1 ) ( T 2 s + 1 ) 1 s = 1 s + 1 T 2 / T 1 − 1 1 s + 1 T 1 + 1 T 1 / T 2 − 1 1 s + 1 T 2 做 拉 普 拉 斯 反 变 换 得 : h ( t ) = 1 + 1 T 2 / T 1 − 1 e − 1 T 1 t + 1 T 1 / T 2 − 1 e − 1 T 2 t \begin{aligned} C(s)&=\Phi(s)R(s)\\ &=\frac{1}{(T_1s+1)(T_2s+1)}\frac{1}{s}\\ &=\frac{1}{s}+\frac{1}{T_2/T_1-1}\frac{1}{s+\frac{1}{T_1}}+\frac{1}{T_1/T_2-1}\frac{1}{s+\frac{1}{T_2}}\\ 做拉普拉斯反变换得:\\ h(t)&=1+\frac{1}{T_2/T_1-1}e^{-\frac{1}{T_1}t}+\frac{1}{T_1/T_2-1}e^{-\frac{1}{T_2}t} \end{aligned}C(s)做拉普拉斯反变换得:h(t)=Φ(s)R(s)=(T1s+1)(T2s+1)1s1=s1+T2/T1−11s+T111+T1/T2−11s+T211=1+T2/T1−11e−T11t+T1/T2−11e−T21t
根据该响应函数可以看出,过阻尼二阶系统得单位阶跃响应函数为单调递增函数,最终趋于1。
对该响应函数分析:
| 指标 | 值 |
|---|---|
| 延迟时间t d t_dtd | 不管 |
| 上升时间t r t_rtr | 不管 |
| 调节时间t s t_sts | 3.3 T 1 ( T 1 = 4 T 2 ) 3 T 1 ( T 1 > 4 T 2 ) ( 5 % ) 3.3T_1(T_1=4T_2)3T_1(T_1>4T_2)(5\%)3.3T1(T1=4T2)3T1(T1>4T2)(5%) |
| 峰值时间t p t_ptp | 无 |
| 超调量σ % \sigma\%σ% | 无 |
| 稳态误差e s s e_{ss}ess | e s s = 0 e_{ss}=0ess=0 |
临界阻尼情况
对于临界阻尼,特征方程有两个相同的实根,即− ζ w n -\zeta w_n−ζwn。此时ζ = 1 \zeta=1ζ=1。
C ( s ) = Φ ( s ) R ( s ) = 1 s − 1 s + w n − w n ( s + w n ) 2 做 拉 普 拉 斯 反 变 换 得 : h ( t ) = 1 − e 1 w n t ( 1 + w n t ) \begin{aligned} C(s)&=\Phi(s)R(s)\\ &=\frac{1}{s}-\frac{1}{s+w_n}-\frac{w_n}{(s+w_n)^2}\\ 做拉普拉斯反变换得:\\ h(t)&=1-e^{1w_nt}(1+w_nt) \end{aligned}C(s)做拉普拉斯反变换得:h(t)=Φ(s)R(s)=s1−s+wn1−(s+wn)2wn=1−e1wnt(1+wnt)
从这个响应函数可以看出,是一个单调递增,最终趋于1的函数。
与过阻尼情况相同,临界阻尼也可以写成两个惯性环节的串联,只不过这两个惯性环节的时间常数相同。
对该响应函数分析:
| 指标 | 值 |
|---|---|
| 延迟时间t d t_dtd | 不管 |
| 上升时间t r t_rtr | 不管 |
| 调节时间t s t_sts | 4.75 T ( 5 % ) 4.75T(5\%)4.75T(5%) |
| 峰值时间t p t_ptp | 无 |
| 超调量σ % \sigma\%σ% | 无 |
| 稳态误差e s s e_{ss}ess | e s s = 0 e_{ss}=0ess=0 |
欠阻尼情况
欠阻尼情况是最为复杂的一种情况。它对应的特征根是一对共轭复根,并且实部不为0。此时0 < ζ < 1 0<\zeta<10<ζ<1。
为了后续分析方便,我们定义阻尼振荡角频率w d = w n 1 − ζ 2 w_d=w_n\sqrt{1-\zeta^2}wd=wn1−ζ2。
C ( s ) = Φ ( s ) R ( s ) = w n 2 s ( s 2 + 2 ζ w n s + w n 2 ) = 1 s − s + ζ w n ( s + ζ w n ) 2 + w d 2 − ζ 1 − ζ 2 w d ( s + ζ w n ) 2 + w d 2 做 拉 普 拉 斯 反 变 换 得 : = 1 − e − ζ w n t ( c o s ( w d t ) − ζ 1 − ζ 2 s i n ( w d t ) ) = 1 − e − ζ w n t 1 − ζ 2 s i n ( w d t + β ) 其 中 , c o s β = ζ \begin{aligned} C(s)&=\Phi(s)R(s)\\ &=\frac{w_n^2}{s(s^2+2\zeta w_ns+w_n^2)}\\ &=\frac{1}{s}-\frac{s+\zeta w_n}{(s+\zeta w_n)^2+w_d^2}-\frac{\zeta}{\sqrt{1-\zeta^2}}\frac{w_d}{(s+\zeta w_n)^2+w_d^2}\\ 做拉普拉斯反变换得:\\ &=1-e^{-\zeta w_nt}(cos(w_dt)-\frac{\zeta}{\sqrt{1-\zeta^2}}sin(w_dt))\\ &=1-\frac{e^{-\zeta w_nt}}{\sqrt{1-\zeta^2}}sin(w_dt+\beta)\\ 其中,cos\beta=\zeta \end{aligned}C(s)做拉普拉斯反变换得:其中,cosβ=ζ=Φ(s)R(s)=s(s2+2ζwns+wn2)wn2=s1−(s+ζwn)2+wd2s+ζwn−1−ζ2ζ(s+ζwn)2+wd2wd=1−e−ζwnt(cos(wdt)−1−ζ2ζsin(wdt))=1−1−ζ2e−ζwntsin(wdt+β)
可以看出,欠阻尼过程的响应函数是一个减幅振荡的过程。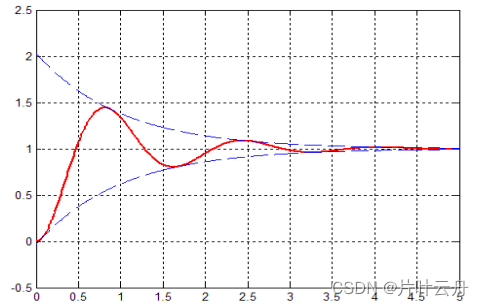
下面分别讨论欠阻尼情况下系统各项性能指标。
上升时间t r t_rtr
此处上升时间指的是从0到第一次到达稳态值的时间。
h ( t ) = 1 − e − ζ w n t 1 − ζ 2 s i n ( w d t + β ) h(t)=1-\frac{e^{-\zeta w_nt}}{\sqrt{1-\zeta^2}}sin(w_dt+\beta)h(t)=1−1−ζ2e−ζwntsin(wdt+β),故第一次到达稳态值即sin第一次为0。故t r = π − β w d t_r=\frac{\pi-\beta}{w_d}tr=wdπ−β。
峰值时间t p t_ptp
对h(t)求导,以获取极大值所对应t,即为峰值时间。
h ( t ) = 1 − e − ζ w n t 1 − ζ 2 s i n ( w d t + β ) 求 导 得 : d h ( t ) d t = w n e − ζ w n t 1 − ζ 2 s i n ( w d t ) \begin{aligned} h(t)&=1-\frac{e^{-\zeta w_nt}}{\sqrt{1-\zeta^2}}sin(w_dt+\beta)\\ 求导得:\\ \frac{dh(t)}{dt}&=\frac{w_ne^{-\zeta w_nt}}{\sqrt{1-\zeta^2}}sin(w_dt) \end{aligned}h(t)求导得:dtdh(t)=1−1−ζ2e−ζwntsin(wdt+β)=1−ζ2wne−ζwntsin(wdt)
令导函数为0,得t p = π w d t_p=\frac{\pi}{w_d}tp=wdπ。
超调量σ % \sigma\%σ%
将t = t p t=t_pt=tp带入即可获得h ( t ) m a x h(t)_{max}h(t)max,即可计算超调量。
h ( t ) m a x = h ( t p ) = 1 − e − ζ w n t p 1 − ζ 2 s i n ( w d t p + β ) = 1 − e − ζ w n t p 1 − ζ 2 s i n ( π + β ) = 1 + e − ζ w n t p 1 − ζ 2 s i n ( β ) = 1 + e − ζ w n t p = 1 + e − ζ π / 1 − ζ 2 故 超 调 量 为 : σ % = h ( t p ) − h ( ∞ ) h ( ∞ ) × 100 % = e − ζ π / 1 − ζ 2 × 100 % \begin{aligned} h(t)_{max}&=h(t_p)=1-\frac{e^{-\zeta w_nt_p}}{\sqrt{1-\zeta^2}}sin(w_dt_p+\beta)\\ &=1-\frac{e^{-\zeta w_nt_p}}{\sqrt{1-\zeta^2}}sin(\pi+\beta)\\ &=1+\frac{e^{-\zeta w_nt_p}}{\sqrt{1-\zeta^2}}sin(\beta)\\ &=1+e^{-\zeta w_nt_p}\\ &=1+e^{-\zeta \pi/\sqrt{1-\zeta^2}}\\ 故超调量为:\\ \sigma\%&=\frac{h(t_p)-h(\infty)}{h(\infty)}\times100\%\\ &=e^{-\zeta \pi/\sqrt{1-\zeta^2}}\times100\% \end{aligned}h(t)max故超调量为:σ%=h(tp)=1−1−ζ2e−ζwntpsin(wdtp+β)=1−1−ζ2e−ζwntpsin(π+β)=1+1−ζ2e−ζwntpsin(β)=1+e−ζwntp=1+e−ζπ/1−ζ2=h(∞)h(tp)−h(∞)×100%=e−ζπ/1−ζ2×100%
调节时间t s t_sts
依据响应函数直接计算调节时间是非常困难的,所以通常采用其包络线进入误差带的时间来近似代替调节时间。即:
e − ζ w n t 1 − ζ 2 = 5 % ( 2 % ) t s = − l n ( 1 − ζ 2 × 5 % ( 2 % ) ) ζ w n \frac{e^{-\zeta w_nt}}{\sqrt{1-\zeta^2}}=5\%(2\%)\\ t_s=-\frac{ln(\sqrt{1-\zeta^2}\times5\%(2\%))}{\zeta w_n}1−ζ2e−ζwnt=5%(2%)ts=−ζwnln(1−ζ2×5%(2%))
通常取近似值,1 − ζ 2 = 1 \sqrt{1-\zeta^2}=11−ζ2=1,l n 0.05 = − 4 ln0.05=-4ln0.05=−4,l n 0.02 = − 3 ln0.02=-3ln0.02=−3。
则5%误差带,t s = 3 ζ w n t_s=\frac{3}{\zeta w_n}ts=ζwn3;2%误差带,t s = 4 ζ w n t_s=\frac{4}{\zeta w_n}ts=ζwn4。
但我们通常采用经验修正后的公式:
t s = 3.5 ζ w n ( 5 % ) t s = 4.5 ζ w n ( 2 % ) t_s=\frac{3.5}{\zeta w_n}(5\%)\\ t_s=\frac{4.5}{\zeta w_n}(2\%)ts=ζwn3.5(5%)ts=ζwn4.5(2%)
平稳性与快速性
从σ % = e − ζ π / 1 − ζ 2 × 100 % \sigma\%=e^{-\zeta \pi/\sqrt{1-\zeta^2}}\times100\%σ%=e−ζπ/1−ζ2×100%和t s = 3.5 ζ w n ( 5 % ) t_s=\frac{3.5}{\zeta w_n}(5\%)ts=ζwn3.5(5%)可以看出,超调量与w n w_nwn无关,只与ζ \zetaζ有关。而调节时间与二者皆有关。
平稳性
对平稳性而言,ζ \zetaζ越大,σ % \sigma\%σ%越小,越平稳。ζ \zetaζ大到1时,变为临界阻尼,就没有超调量了。ζ \zetaζ小到0时,变为无阻尼,超调量100%了。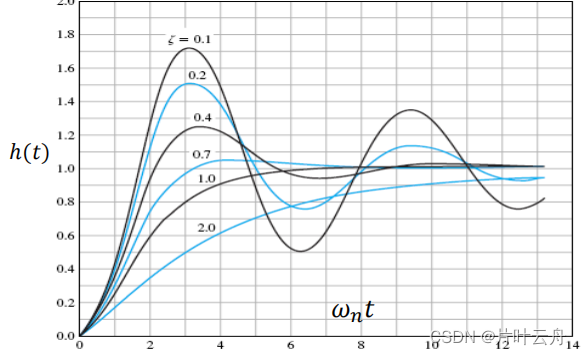
快速性
对于调节时间而言,一般取ζ = 0.707 \zeta=0.707ζ=0.707左右时,超调时间最短。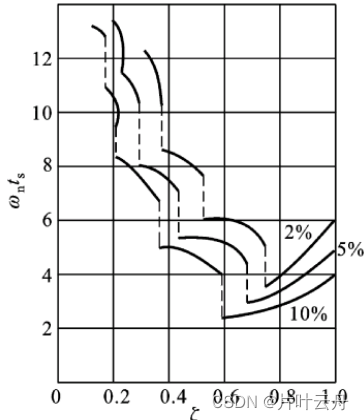
同时,ζ \zetaζz一定时,w n w_nwn越大,调节时间越短。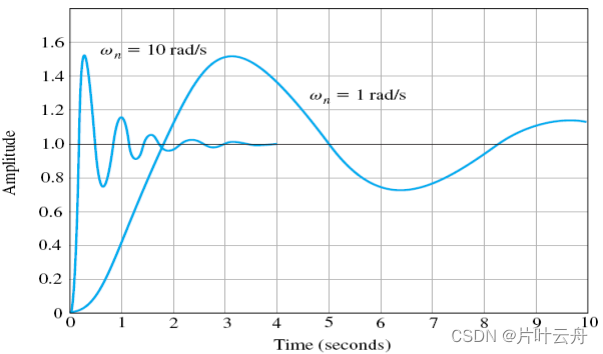
对欠阻尼响应函数分析,总结如下:
| 指标 | 值 |
|---|---|
| 延迟时间t d t_dtd | 不管 |
| 上升时间t r t_rtr | π − β w d \frac{\pi-\beta}{w_d}wdπ−β |
| 调节时间t s t_sts | 3.5 ζ w n ( 5 % ) 4.5 ζ w n ( 2 % ) \frac{3.5}{\zeta w_n}(5\%)\frac{4.5}{\zeta w_n}(2\%)ζwn3.5(5%)ζwn4.5(2%) |
| 峰值时间t p t_ptp | π w d \frac{\pi}{w_d}wdπ |
| 超调量σ % \sigma\%σ% | e − ζ π / 1 − ζ 2 × 100 % e^{-\zeta \pi/\sqrt{1-\zeta^2}}\times 100\%e−ζπ/1−ζ2×100% |
| 稳态误差e s s e_{ss}ess | e s s = 0 e_{ss}=0ess=0 |
无阻尼情况
分析完欠阻尼情况,无阻尼情况就比较简单。无阻尼情况对应特征根为实部为0的共轭复根。ζ = 0 \zeta=0ζ=0。
C ( s ) = Φ ( s ) R ( s ) = w n 2 s 2 + w n 2 1 s = 1 s − s s 2 + w n 2 做 拉 普 拉 斯 反 变 换 得 : h ( t ) = 1 − c o s ( w n t ) \begin{aligned} C(s)&=\Phi(s)R(s)\\ &=\frac{w_n^2}{s^2+w_n^2}\frac{1}{s}\\ &=\frac{1}{s}-\frac{s}{s^2+w_n^2}\\ 做拉普拉斯反变换得:\\ h(t)&=1-cos(w_nt) \end{aligned}C(s)做拉普拉斯反变换得:h(t)=Φ(s)R(s)=s2+wn2wn2s1=s1−s2+wn2s=1−cos(wnt)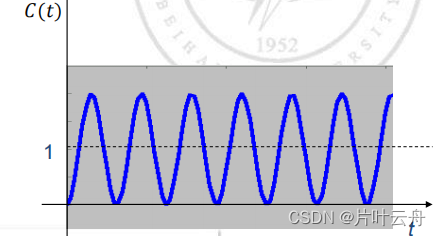
| 指标 | 值 |
|---|---|
| 超调量σ % \sigma\%σ% | 100 % 100\%100% |
一阶、二阶系统改进措施
未完待续