RMQ和LCA在线算法

原文
学习一下LCA的在线算法。

RMQ

RMQ是查询区间最值的一种方法，其思想非常简单。举例来说，我们想查询区间$[5,37]$中的最小值，如果我们事先知道区间$[5,5+2^4)$中的最小值以及区间$[37-2^4+1,37+1)$中的最小值，那么我们很容易得到答案。于是问题就变为，我们如何知道区间$[i,i+2^k)$中的最小值。显然

$$Min([i,i+2^k)) = min(Min([i,i+2^{(k-1)}),Min([i+2^{k-1},i+2^k))$$

这样，我们就能利用DP达到目的，上式便是状态转移方程。

$dp(i,j)$表示区间$[i,i+2^j)$中的最小值，根据状态转移方程有：$dp(i,j) = min(dp(i,j-1),dp(i+(1<<j-1),j-1)$

于是，初始化dp的代码如下

void RMQININT(int n){
    for(int i = 0 ;i<=n ;i++){
        dp[i][0] = i ;
    }
    for(int j = 1 ;1<<j<=n ;j++){
        //这里减一的原因是右区间为开区间
        for(int i = 0 ;i+(1<<j)-1<=n;i++){
            int x = dp[i][j-1];
            int y = dp[i+(1<<(j-1))][j-1] ;
            dp[i][j] = min(x,y);
        }
    }

}

查询区间$[L,R]$中的最小值也非常简单

$$ans = min(Min([L,L+2^k),Min([R-2^k+1,R+1))$$

其中$k$为使得$L+2^{k+1}<=R+1$满足的最大值。查询的代码如下

int RMQ(int L ,int R){
    int k ;
    while(L+(1<<(k+1)) <= R+1)k++;
    int x = dp[L][k];
    int y = dp[R-(1<<k)+1][k] ;
    return min(x,y) ;
}

LCA在线算法

LCA的概念想必不用多说，求LCA的算法分为在线和离线两种，在线算法就是对于每一次算法求一次LCA，离线算法就是将所有查询离线保存下来，进行批量查询。本文直介绍在线的ST算法。

ST算法是个非常容易理解的算法，实现也非常简单。举例说明：

假设现在有这么一棵树：

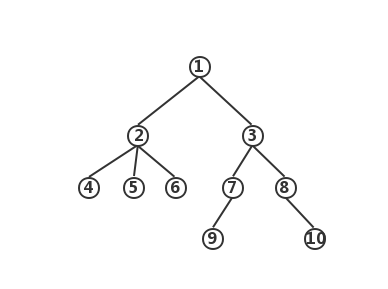
我想查询节点4和节点10的最近公共祖先。

首先，我们从节点1开始，深度优先搜索这棵树，深搜的顺序为:

1 $\rightarrow$2$\rightarrow$4$\rightarrow$2$\rightarrow$5$\rightarrow$2$\rightarrow$6$\rightarrow$2$\rightarrow$1$\rightarrow$3$\rightarrow$7$\rightarrow$9$\rightarrow$7$\rightarrow$3$\rightarrow$8$\rightarrow$10

这个序列貌似可以称之为欧拉序列，在深搜的同时，我们保存一下每个节点第一次出现在欧拉序列中的位置first[],以及欧拉序列每一个位置对应的节点在树中的深度，这些信息在后面会用到。

求4和10的最近公共祖先的步骤也比较简单。通过深搜，我们知道，4第一次出现在欧拉序列中的位置为3；10第一次出现在欧拉序列中的位置为16。那么4和10的最近公共祖先就是欧拉序列第3位到第16位的节点中，深度最小的那一个。求深度最小的节点，可以采用RMQ。

那么为什么这么做就能够得到LCA呢，其实道理很简单，dfs得到的欧拉序列中，任意一段都是整棵树的一棵子树，并且这棵子树必定是包含待查询的两点的最小子树（这里说的最小，不考虑不包含待查询点的分叉)，这也就说明，该子树中深度最小的点必定为待查询两点的最近公共祖先。

代码