传统的朴素模式匹配算法
由于主串指针i回溯,且每次只前进一个距离,没有减少不必要的匹配过程。故效率非常低。
KMP算法
与朴素模式匹配算法不同,kmp巧妙的利用了当前c字符失配而c字符前面的字符都成功匹配
的信息,因此可跳过某些不必要的匹配。kmp将关注点落在了模式串t的有效信息提取上,与主串s
无关,故消除了主串s的回溯
1.kmp的重点就落在对模式串t的有效信息提取上即最长公共前后缀next数组
next数组是kmp算法的核心
next数组用以保存当前字符c之前子串的最长公共前后缀的信息
- 手算next数组
模式串t:g o o g l e
| 前缀集(不含最后字符) | 后缀集(不含开始字符) | 交集元素个数 | |
|---|---|---|---|
| g | 空集 | 空集 | 0 |
| go | {g} | {o} | 0 |
| goo | {g,go} | {o,oo} | 0 |
| goog | {g,go,goo} | {g,og,oog} | 1 |
| googl | {g,go,goo,goog} | {l,gl,ogl.oogl} | 0 |
| {g,go,goo,goog,googl} | {e,le,gle,ogle,oogle} | 0 |
| 模式串t | g | o | o | g | l | e |
|---|---|---|---|---|---|---|
| next数组 | 0 | 0 | 0 | 1 | 0 | 0 |
利用next数组匹配
如上图当在字符 l 处发生匹配失败时,可知前面所有的字符已匹配成功。此时我们可能会想如果把模式串向右移使第一个字符g对齐匹配失败的前一个字符就好了。
没错这就是kmp算法的核心利用最长公共前后缀减少不必要的匹配过程
那么问题来了,将模式串向右移,移多少呢?这时候我们之前提到的提取有效信息next数组就发挥作用了。
我们需要将失配之前的最长公共前缀部分移动到后缀部分,也就是如下图这样。

移动公式:
move = 指针j之前匹配成功个数 - next[j-1] //将前缀移动到后缀处
= (j-1) - next[j-1]
将比较指针j回退到
j = j-move
= j - ((j-1)-next[j-1]) = next[j-1]+1
kmp模式串利用next数组匹配的核心 (j如何回退,回退到哪)
至此最重要的信息我们知道了,当字符c匹配失败后比较指针j回退到j = next[j-1]+1
即与失配指针j之前后缀字符相同的前缀后一个字符
也许我们还可以再做进一步改进
将next数组整体右移一位,低位补 -1
好处是 回退指针j 不要参照 j之前j-1处的值, 而是变成了 j = next[j]+1直接由当前失配字符下标得出
| 模式串t | g | o | o | g | l | e |
|---|---|---|---|---|---|---|
| next数组 | 0 | 0 | 0 | 1 | 0 | 0 |
| 模式串t | g | o | o | g | l | e |
|---|---|---|---|---|---|---|
| next数组 | -1 | 0 | 0 | 0 | 1 | 0 |
也许有些同学已经看出来了,既然直接通过当前字符得出回退位置,那为什么不把
j = next[j]+1 改写成 j = next[j] 呢?只需要将next数组整体+1即可。于是next最终变成这样。
| 模式串t | g | o | o | g | l | e |
|---|---|---|---|---|---|---|
| next数组 | 0 | 1 | 1 | 1 | 2 | 1 |
next数组优化
为什么要优化?在以下例子中你将会明白

由于当前位置失配后,与前面匹配成功与当前位置相同的字符必然也会失配,故会造成无效匹配。
故优化为:若 字符c的next处的字符与c相同则置为前者的nextval值,不同则不变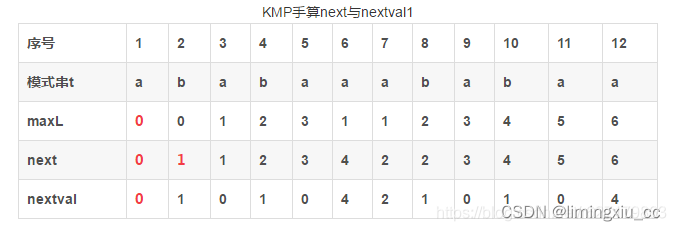
代码实现部分
- 获取next
public static void getNext(String t,int next[]){
int i=0; //模式串指针
int j=-1;
next[0] = -1;
while(i<t.length()-1){
if(j==-1||t.charAt(i)==t.charAt(j)){
next[++i] = ++j;
}else{
j = next[j];
}
}
}
- 获取nextval
public static void getNextVal(String t,int nextval[]){
int i=0;
int j=-1;
nextval[0] = -1;
while(i<t.length()-1){
if(j==-1||t.charAt(i)==t.charAt(j)){
++i;
++j;
if(t.charAt(i)!=t.charAt(j)) nextval[i]=j;
else nextval[i]=nextval[j];
}else{
j = nextval[j];
}
}
}
- kmp实现
public static void kmp(String s,String t){
int[] next = new int[t.length()];
getNext(t,next);
int i = 0, j = 0;
while (i < s.length() && j < t.length()) {
if (j == -1 || s.charAt(i) == t.charAt(j)) {
i++;
j++;
}
else j = next[j];
if (j >= t.length()) {//匹配所有
// return i - t.length();//匹配第一次出现的子串
System.out.println(i - t.length());
j=0;//重置
}
}
}
版权声明:本文为qq_39643546原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。
