最近我们被客户要求撰写关于正态性、收敛性的研究报告,包括一些图形和统计输出。
在我们的数理统计课程中,已经看到了大数定律(这在概率课程中已经被证明),证明
![]()
给出一组i.i.d.随机变量 ![]() ,其中有
,其中有
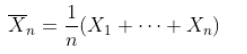
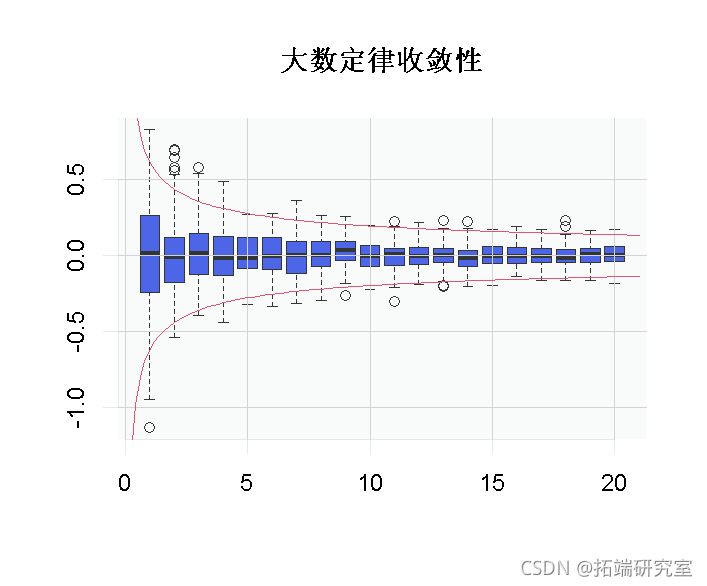
为了直观地看到这种收敛性,我们可以使用
> for(i in 1:20)B[,i]=mean_samples(i*10)
> boxplot(B)也可以直观地看到边界 ![]() (用于中心极限定理,获得极限的非退化分布)。
(用于中心极限定理,获得极限的非退化分布)。
我们一直在讨论经验累积分布函数的特点。
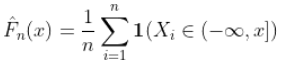
我们已经看到了格利文科-坎特利定理,该定理指出
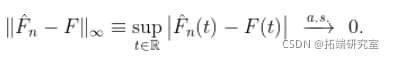
为了直观地看到这种收敛。这里我使用了一个技巧可视化
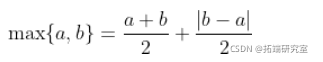
获得两个矩阵之间的最大值(分量)。
+ Df=(D1+D2)/2+abs(D2-D1)/2
> boxplot(B)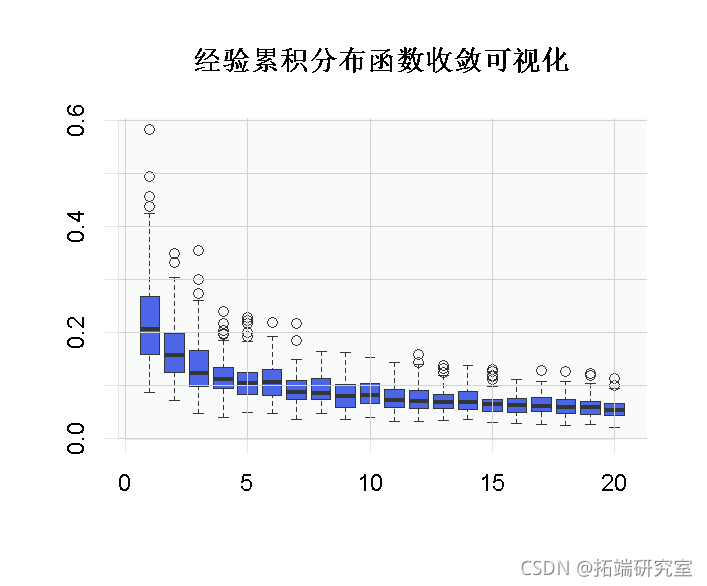
我们还讨论了经验累积分布函数的逐点渐近正态性
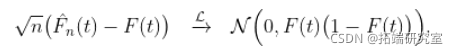
在这里,又可以把它形象化。第一步是计算经验累积分布函数的几条轨迹
> plot(u,u)
请注意,我们可以计算(逐点)置信带
> lines(u,apply(M,1,function(x) quantile(x,.05)
> lines(u,apply(M,1,function(x) quantile(x,.95)
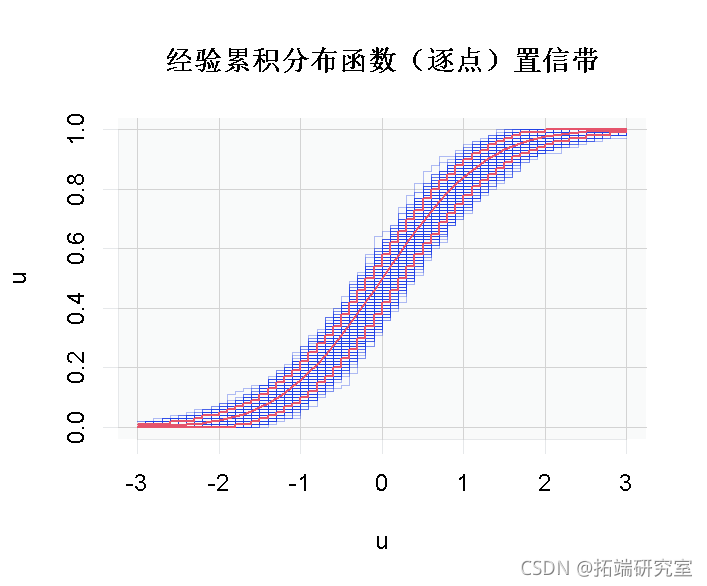
现在,如果我们专注于一个特定的点,我们可以直观地看到渐近正态性(即当我们有一个大小为100的样本时,几乎是正态的)。
> hist(y)
> lines(vu,dnorm(vu,pnorm(x0)
+ sqrt((pnorm(x0)*(1-pnorm(x0)))/100)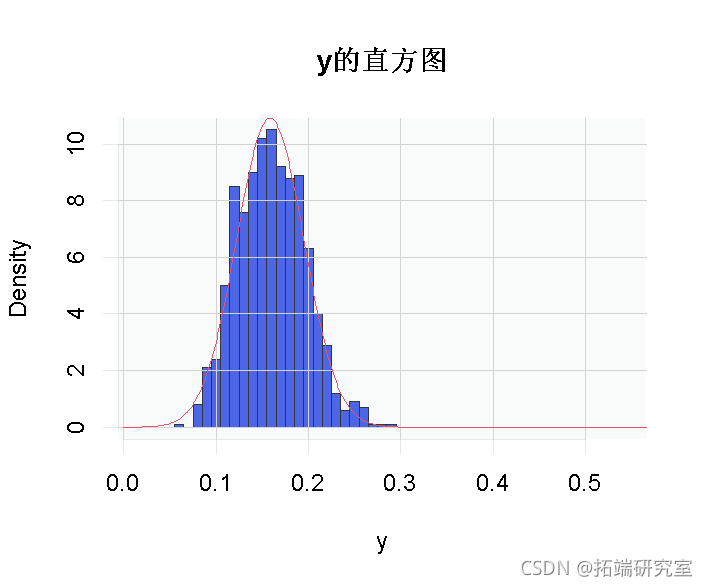

版权声明:本文为qq_19600291原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。