原因如下

B+树能显著减少IO次数，提高效率
B+树的查询效率更加稳定，因为数据放在叶子节点
B+树能提高范围查询的效率，因为叶子节点指向下一个叶子节点

介绍

从一堆数据中查找指定的数据时，我们常用的数据结构是哈希表和二叉查找树，表本质上就是一堆数据的集合，所以MySQL数据库用了哈希表和B+树来实现索引

B+树是通过二叉查找树，再由平衡二叉树，B树（又名B-树）演化而来的，B+树中的B不是代表二叉（binary），而是代表平衡（balance），因为B+树是从最早的平衡二叉树演化而来，但是B+树不是一个二叉树。

二叉查找树和平衡二叉树

二叉查找树的效率和平衡二叉树的查找效率已经很高了，为什么不用这两种数据结构来实现索引呢

二叉查找树是带有特殊属性的二叉树，需要满足以下属性

非叶子节点最多拥有两个子节点
非叶子节值大于左边子节点、小于右边子节点
没有值相等重复的节点;

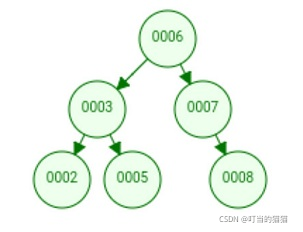
查键值为5的记录，先找到根，其值时6，大于5，查找6的左子树，找到3，5大于3，再找其右子树，一共找了3次。同理，查找键值为8的记录，用了3次。所有键值平均查找次数为(1+2+2+3+3+3)/6=2.3次

二叉查找树可以任意的构造，假如二叉查找树按照如下方式构造

平均查找速度为(1+2+3+4+5+5)/6=3.16次。为了提高二叉查找树的查询效率，需要二叉查找数是平衡的。

平衡二叉树除了满足上面3个属性，还要满足如下1个属性

树的左右两边的层级数相差不会大于1

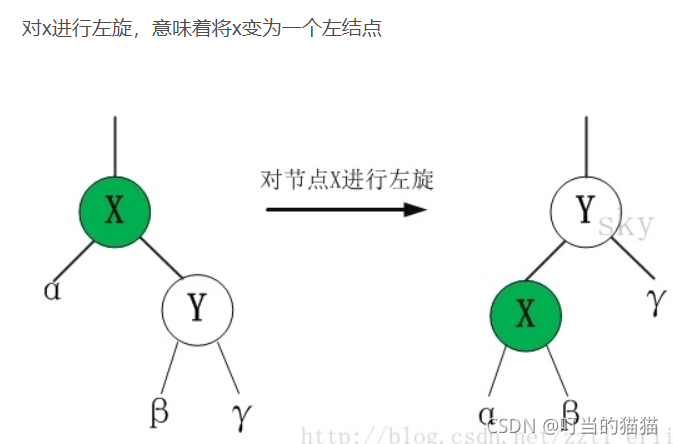
平衡二叉树的查找效率确实很快，但维护一颗平衡二叉树的代价是非常大的，需要1次或多次左旋和右旋来得到插入或更新后树的平衡性。

B树和B+树

磁盘的IO次数

B树和B-树是同一种树，假如用平衡二叉树实现索引效率已经很高了，查找一个节点所做的IO次数是这个节点所处的树的高度，因为我们无法把整个索引都加载到内存，并且节点数据在磁盘中不是顺序排放的。所以最快情况下，磁盘的IO次数为树的高度。

虽然平衡二叉树查找效率确实很高，但是频繁的IO才是阻碍提高性能的瓶颈，怎样减少IO次数呢？前辈们很聪明的提出了局部性原理分为

时间局部性原理，即加入你查询id为1的用户数据，过一段时间你还会查询id为1的数据，所以会将这部分数据缓存下来。

空间局部性原理，当你查询id为1的用户数据的时候，你有很大的概率会去查询id为2，3，4的用户的数据，所以会一次性的把id为1，2，3，4的数据都读到内存中去，这个最小的单位就是页。

树高决定着IO的次数，那么降低树高不就能减少IO的次数吗，怎么减少呢，每个节点的数据多放一点不就行了

树

B树也就是B-树，B树是一个多路搜索树，也就是每个节点可以有多个子节点，这样是为了降低树的高度，减少磁盘IO次数

B+树是B树的优化，他的子节点只存储键而不存储数据，数据全部存在叶子节点，并且叶子节点间通过指针进行连接，这样因为子节点不存储数据，那么磁盘可以一次读取更多的子节点，减少IO次数，并且叶子节点想通，如果想查询10-100的数据只需要找到头尾就可以了。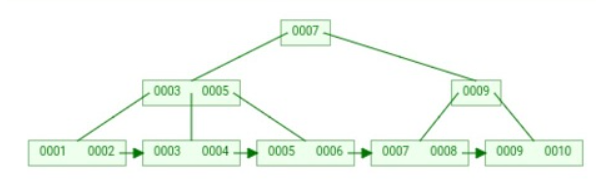

B和B+区别

1. B+树的非叶子节点不保存键值对应的数据，这样使得B+树每个节点所能保存的键值大大增加；
2. B+树叶子节点保存了父节点的所有键值和键值对应的数据，每个叶子节点的关键字从小到大链接；
3. B+树的根节点键值数量和其子节点个数相等;
4. B+的非叶子节点只进行数据索引，不会存实际的键值对应的数据，所有数据必须要到叶子节点才能获取到，所以每次数据查询的次数都一样；
   
   B+每个节点存储的关键字数更多，树的层级更少所以查询数据更快，所有关键字指针都存在叶子节点，所以每次查找的次数都相同所以查询速度更稳定。

除此之外，B+树的叶子节点是跟后序节点相连接的，这对范围查找是非常有用的。

B+是多路平衡查询树，所以他的节点是天然有序的（左子节点小于父节点、父节点小于右子节点），所以对于范围查询的时候不需要做全表扫描。