KMP模式匹配算法

1 KMP模式匹配算法原理

假设主串S=“abcdefab”，我们要匹配的子串T=”abcdex“，如果用朴素模式匹配算法，前5个字母，两个串完全相等，直到第6个字母，”f“与“x”不等，如图所示。

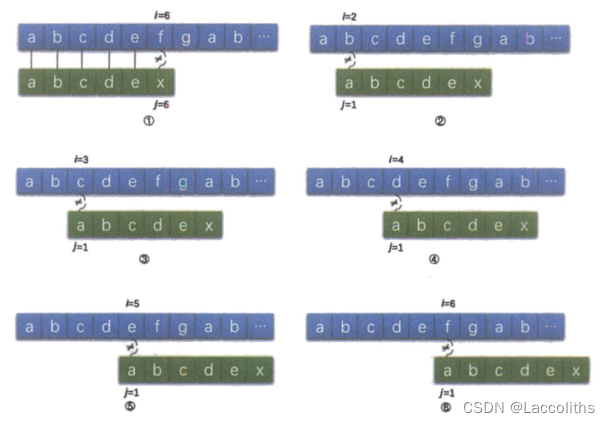
接下来按照朴素模式匹配算法，应该是按照上图的步骤2、3、4、5、6，即主串S中当$i=2、3、4、5、6$时，首字符与子串T的首字符均不等。

仔细观察就会发现，对于要匹配的子串T来说，“abcdex”首字母“a”与后面串“bcdex”中任意一个字符都不相等。也就是说对于步骤1来说前五位字符分别相等，意味着子串T的首字符“a”不可能与S串的第2位到第5位字符相等。所以，在上图中，步骤2、3、4、5的判断都是多余的。

当我们知道T串中首字符“a”与T中后面的字符均不相等的前提下，T串后面的字符均不相等的前提下，T串的“a”与S串后面的“c”“d”“e”也都可以在步骤1之后就可以确定是不相等的，所以在朴素模式匹配算法中步骤2、3、4、5没有必要，只保留步骤1、6即可，如图所示。

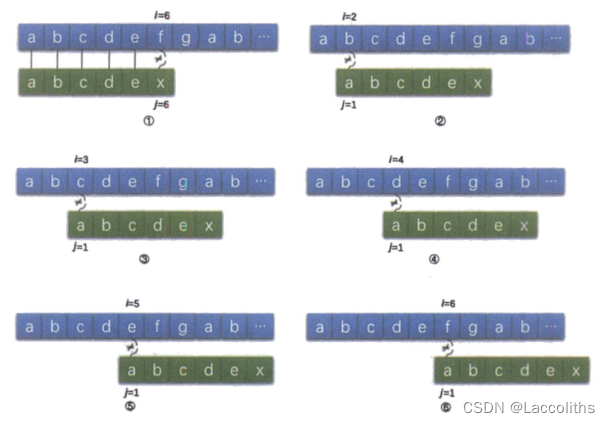
保留步骤6中的判断是因为在步骤1中$T[6]\ne S[6]$，虽然我们已经知道了$T[1]\ne T[6]$，也不能断定$T[1]$一定不等于$S[6]$，因此只需要保留步骤6这一步。

对于在子串中有与首字符相等的字符，也是可以省略一部分不必要的判断步骤，如图所示，省略T串前两位“a”与“b”同S串中的4、5位置字符匹配操作。

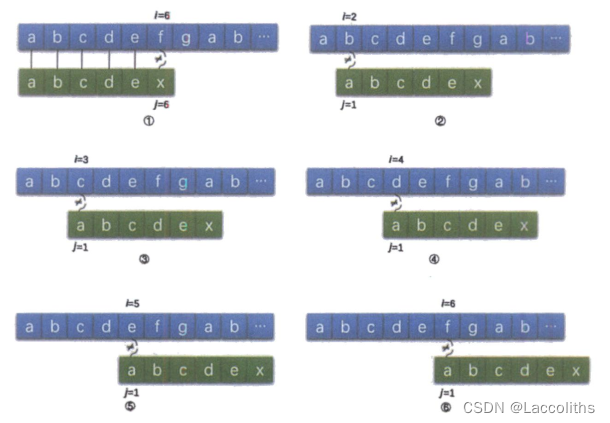
在朴素的模式匹配算法中，主串的i值是不断地回溯来完成的，而这种回溯其实是可以省略的，KMP模式匹配算法就是为了让这没必要的回溯不发生。

既然i值不回溯，也就是不可以变小，那要考虑的变化就是j值了，通过观察可以发现，提到了T串的首字符与自身后面字符的比较，发现如果有相等字符，j值的变化就会不相同。也就是说，j值的变化与主串其实没什么关系，关键取决于T串的结构中是否有重复问题，j值的大小取决于当前字符的串的前后缀的相似度。

在需要查找字符串前，先对要查找的字符串做一个分析，这样可以大大减少我们查找的难度，提高查找的速度。

KMP算法：不回溯，从最长相等前后缀后面一个字符开始比较。

2 KMP算法字符串的前缀、后缀、最长相等前后缀

前缀：包含第一个字符，但不包含最后一个字符的子串。

后缀：包含最后一个字符，但不包含第一个字符的子串。

最长相等前后缀：前缀和后缀相等的最长子串。

例如字符串“abca”

• 前缀：{a,ab,abc}
• 后缀：{a,ca,bca}
• 最长相等前后缀：a

字符串“ababa”

• 前缀：{a,ba,aba,abab}
• 后缀：{a,ba,aba,baba}
• 最长相等前后缀：aba

3 next数组的推导

当$S_i$和$T_j$发生失配时，i不回溯，下一趟让j指向最长相等前后缀的后一个位置，用数组将这一位置记录下来，即为next数组。

假设模式串T=“ababaaaba”，如图所示。

1. 当j=1时，第一位默认为0或-1，next[1]=0。

2. 当j=2时，next[2]=1。

3. 当j=3时，next[3]=1。

4. 当j=4时，j由1到j-1的串是“aba”，next[4]=2。

   前缀字符：{a,ab}

   后缀字符：{a,ba}

   最长相等前后缀：{a}

5. 当j=5时，j由1到j-1的串是“abab”，next[5]=3。

   前缀字符：{a,ab,aba}

   后缀字符：{b,ab,bab}

   最长相等前后缀：{ab}

6. 当j=6时，j由1到j-1的串是“ababa”，next[6]=4。

   前缀字符：{a,ab,aba,abab}

   后缀字符：{a,ba,aba,baba}

   最长相等前后缀：{aba}

7. 当j=7时，j由1到j-1的串是“ababaa”，next[7]=2。

   前缀字符：{a,ab,aba,abab,ababa}

   后缀字符：{a,aa,baa,abaa,babaa}

   最长相等前后缀：{a}

8. 当j=8时，j由1到j-1的串是“ababaaa”，next[8]=2。

   前缀字符：{a,ab,aba,abab,ababa,ababaa}

   后缀字符：{a,aa,aaa,baaa,abaaa,babaaa}

   最长相等前后缀：{a}

9. 当j=9时，j由1到j-1的串是“ababaaab”，next[9]=3。

   前缀字符：{a,ab,aba,abab,ababa,ababaa,ababaaa}

   后缀字符：{b,ab,aab,aaab,baaab,abaaab,babaaab}

   最长相等前后缀：{ab}

4 KMP模式匹配算法的实现

next数组算法：

void get_next(String T,int *next){
    int i,k;
    i=1;
    k=0;
    next[1]=0;
    while(i<T[0]){  // T[0]表示串T的长度
        if(k==0 || T[i]==T[k]){
            ++i;
            ++k;
            next[i] = k;
        }else{
            k = next[k]; // 若字符不相同，则k回溯
        }
    }
}

KMP算法实现：

/* 返回子串T在主串S中第pos个字符之后的位置。若不存在，则函数返回值为0。 */
/*  T非空，1≤pos≤StrLength(S)。 */
int Index_KMP(String S, String T, int pos){
    int i = pos;		/* i用于主串S中当前位置下标值，若pos不为1，则从pos位置开始匹配 */
    int j = 1;			/* j用于子串T中当前位置下标值 */
    int next[255];		/* 定义一next数组 */
    get_next(T, next);	/* 对串T作分析，得到next数组 */
    while (i <= S[0] && j <= T[0]) { /* 若i小于S的长度并且j小于T的长度时，循环继续 */
        if (j==0 || S[i] == T[j]) {  /* 两字母相等则继续，与朴素算法增加了j=0判断 */
            ++i;
            ++j;
        }else{  /* 指针后退重新开始匹配 */
            j = next[j];/* j退回合适的位置，i值不变 */
        } 			
    }
    if (j > T[0]) {
        return i - T[0];
    }else{
        return 0;
    }
}

对于get_next函数来说，若T的长度为m，因只涉及简单的单循环，其时间复杂度为$O(m)$，而由于i值的不回溯，使得index_KMP算法效率得到了提高，while循环的时间复杂度为$O(n)$。因此，整个算法的时间复杂度为$O(n+m)$。相较于朴素模式的匹配算法的$O((n-m+1)\ast m)$来说，是要好一些的。

5 改进KMP模式匹配算法

KMP算法还是有缺陷的，如果主串S=“aaaabcde”，子串T=“aaaaax”，其next数组值分别为012345，KMP算法匹配过程如图所示。

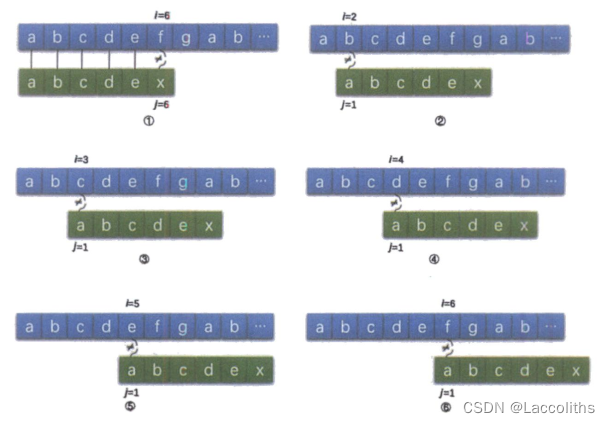
在开始时，当i=5,j=5时，发现“b”与“a”是不相等的，如步骤1所示，此时j=next[5]=4，如步骤2，此时“b”与第4位置的“a”依然不等，j=next[4]=3，如步骤3所示，后依次是步骤4、5，直到j=next[1]=0，此时i++,j++，得到i=6,j=1,如步骤6所示。

我们发现，当中的步骤2、3、4、5都是多余的判断。由于T串的第2、3、4位置的字符都与收尾的“a”相等，那么可以用首位next[1]的值去取代与它相等的字符后续next[j]的值。

假设取代的数组为nextval，改进KMP_nextval数组代码如下：

/* 求模式串T的next函数修正值并存入数组nextval */
void get_nextval(String T, int *nextval)
{
    int i,k;
    i=1;
    k=0;
    nextval[1]=0;
    while (i<T[0])  /* 此处T[0]表示串T的长度 */
    {
        if(k==0 || T[i]== T[k])
        {
            ++i;
            ++k;
            if (T[i]!=T[k]){   /* 若当前字符与前缀字符不同 */
                nextval[i] = k;	/* 则当前的j为nextval在i位置的值 */
            }else{
                nextval[i] = nextval[k];	/* 如果与前缀字符相同，则将前缀字符的 */
                                            /* nextval值赋值给nextval在i位置的值 */
            }
        }
        else{
            k= nextval[k];			/* 若字符不相同，则k值回溯 */
        }
    }
}

6 nextval数组值推导

假设T=“ababaaaba”，先计算出next数组的值分别为011234223，然后再分别判断，如图所示。

1. 当j=1时，nextval[1]=0。

2. 当j=2时，因第二位字符“b”的next值为1，而第一位就是“a”，他们不等，所以nextval[2]=next[2]=1，维持原值。

3. 当j=3时，因为第三位字符“a”的next值为1，所以与第一位的“a”比较得知他们相等，所以nextval[3]=nextval[1]=0，如图所示。
   

4. 当j=4时，因为第三位字符“b”的next值为2，所以与第二位的“b”比较得知他们相等，所以nextval[4]=nextval[2]=1，如图所示。

5. 当j=5时，next值为3，第五个字符“a”与第三位的“a”比较得知他们相等，所以nextval[5]=nextval[3]=0。

6. 当j=6时，next值为4，第六个字符“a”与第四位的“b”比较得知他们不相等，所以nextval[6]=4。

7. 当j=7时，next值为2，第七个字符“a”与第二位的“b”比较得知他们不相等，所以nextval[7]=2。

8. 当j=8时，next值为2，第八个字符“b”与第二位的“b”比较得知他们相等，所以nextval[8]=nextval[2]=1。

9. 当j=9时，next值为3，第九个字符“a”与第三位的“a”比较得知他们相等，所以nextval[9]=nextval[3]=0。