第二十次CCF计算机软件能力认证

A. 检测点查询

题意

求n nn个点中距离关键点最近的三个点。
若距离相同，则取编号小的。
3 ≤ n ≤ 200 , 0 ≤ ∣ x ∣ , ∣ y ∣ ≤ 200 3\le n\le 200,0\le|x|,|y|\le2003≤n≤200,0≤∣x∣,∣y∣≤200

题解

分别记录最小值，次小值，第三小值即可。
时间复杂度O ( n ) O(n)O(n)

#include <bits/stdc++.h>
#define sqr(x) ((x) * (x))
using namespace std;
typedef pair<int, int> Pii;
int n;
struct Point { int x, y; } p, q;
Pii m1 = {INT32_MAX, 0}, m2 = m1, m3 = m1;
inline int dis2(Point a, Point b) { return sqr(a.x - b.x) + sqr(a.y - b.y); }
inline void Ins(Pii x) {
    if (x < m1) m3 = m2, m2 = m1, m1 = x;
    else if (x < m2) m3 = m2, m2 = x;
    else if (x < m3) m3 = x;
}
int main() {
    scanf("%d%d%d", &n, &q.x, &q.y);
    for (int i = 1; i <= n; ++i)
        scanf("%d%d", &p.x, &p.y), Ins({dis2(p, q), i});
    printf("%d\n%d\n%d", m1.second, m2.second, m3.second);
    return 0;
}

B. 风险人群筛查

题意

给定一个矩形左下角和右上角的坐标。
有n nn个人，给定这n nn个人在1 ∼ t 1\sim t1∼t时刻的坐标。
求有多少人某时刻在出现矩形内；求有多少人至少连续k kk个时刻在矩形内（边界也算）。
1 ≤ n ≤ 20 , 1 ≤ k ≤ t ≤ 1 0 3 1\le n\le20,1\le k\le t\le10^31≤n≤20,1≤k≤t≤103

题解

第一问直接判断；第二问判断每个人在矩形内的最长连续时间是否大于等于k kk即可。
时间复杂度O ( n t ) O(nt)O(nt)

#include <bits/stdc++.h>
using namespace std;
int n, k, t, Ans1, Ans2;
struct Point {
    int x, y;
    inline void init() { scanf("%d%d", &x, &y); }
    inline bool operator<=(const Point b) { return x <= b.x && y <= b.y; }
} LD, RU, p;
int main() {
    scanf("%d%d%d", &n, &k, &t);
    LD.init(), RU.init();
    while (n--) {
        int flag = 0, maxL = 0, L = 0;
        for (int i = 1; i <= t; ++i) {
            p.init();
            if (LD <= p && p <= RU)
                flag = 1, ++L;
            else
                maxL = max(maxL, L), L = 0;
        }
        maxL = max(maxL, L);
        Ans1 += flag, Ans2 += maxL >= k;
    }
    printf("%d\n%d", Ans1, Ans2);
    return 0;
}

C. 点亮数字人生

题意

给定一个包含n nn个节点的逻辑电路，每个节点有一个算符（N O T , X O R , A N D , O R , N A N D , N O R \rm NOT,XOR,AND,OR,NAND,NORNOT,XOR,AND,OR,NAND,NOR），共有m mm个输入端，每个节点至多有k kk个输入源。
S SS组询问，给定所有m mm个输入源的输入值0 / 1 0/10/1和s o s_oso​个节点的编号s 1 , s 2 , . . . , s s o s_1,s_2,...,s_{s_o}s1​,s2​,...,sso​​。
若逻辑电路存在环，则输出L O O P \rm LOOPLOOP；否则对于每组询问，求出节点s 1 , s 2 , . . . , s s o s_1,s_2,...,s_{s_o}s1​,s2​,...,sso​​的结果。
Q QQ组数据。
Q ≤ 5 , n ≤ 500 , k ≤ 5 , m ≤ k n , S ≤ 1 0 4 Q\le5,n\le500,k\le5,m\le kn,S\le10^4Q≤5,n≤500,k≤5,m≤kn,S≤104
样例一对应的逻辑电路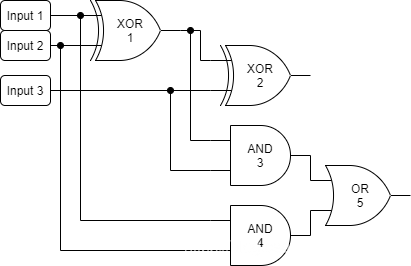：在这里插入图片描述

题解

根据输入的关系建立出相应的有向图（所有的输入源也当成一个点），利用拓扑排序直接求解即可。
时间复杂度O ( Q S ( n + m ) ) O(QS(n+m))O(QS(n+m))

#include <bits/stdc++.h>
using namespace std;
const int N = 3000 + 5;
typedef int arr[N];
int n, m, S, Cnt, Loop;
arr in, deg, op, Ans, s_;
vector<int> G[N], input[N];
vector<int> I_[10005];
inline int f(vector<int> input, int op) {
    int y = 0;
    if (!op) return !input[0]; // NOT
    else if (op == 1) {   // XOR
        for (auto x : input)
            y ^= x;
        return y;
    } else if ((op | 1) == 3) { // AND,NAND
        y = input[0];
        for (int i = 1; i < (int)input.size(); ++i)
            y &= input[i];
        return op & 1 ? !y : y;
    } else { // OR,NOR
        for (auto x : input)
            y |= x;
        return op & 1 ? !y : y;
    }
}
inline void Topsort() {
    if (Loop == 1)
        return;
    queue<int> q;
    for (int i = 1; i <= n; ++i)
        deg[i] = in[i], input[i].clear();
    for (int i = n + 1; i <= n + m; ++i)
        q.push(i);
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        for (auto v : G[u]) {
            input[v].push_back(Ans[u]);
            if (!(--deg[v]))
                Ans[v] = f(input[v], op[v]), q.push(v);
        }
    }
    if (Loop == -1) {
        for (int i = 1; i <= n; ++i)
            if (deg[i])
                return (void)(Loop = 1, puts("LOOP"));
        Loop = 0;
    }
    for (int i = 1; i <= Cnt; ++i)
        printf("%d%c", Ans[s_[i]], " \n"[i == Cnt]);
}
inline int GetOP(char *s) {
    if (s[0] == 'O') return 4;
    if (s[0] == 'X') return 1;
    if (s[0] == 'A') return 2;
    if (s[1] == 'A') return 3;
    if (s[2] == 'T') return 0;
    return 5;
}
inline void Solve() {
    for (int i = 1; i <= n + m; ++i)
        in[i] = 0, G[i].clear();
    for (int i = 1; i <= n; ++i) {
        char s[5];
        int u;
        scanf("%s%d", s, &in[i]);
        op[i] = GetOP(s);
        for (int j = 1; j <= in[i]; ++j) {
            scanf("%s", s);
            if (s[0] == 'O')
                sscanf(s, "O%d", &u), G[u].push_back(i);
            else
                sscanf(s, "I%d", &u), G[n + u].push_back(i);
        }
    }
    Loop = -1;
    scanf("%d", &S);
    for (int i = 1; i <= S; ++i) {
        I_[i].resize(m);
        for (int j = 0; j < m; ++j)
            scanf("%d", &I_[i][j]);
    }
    for (int i = 1; i <= S; ++i) {
        for (int j = n + 1; j <= n + m; ++j)
            Ans[j] = I_[i][j - n - 1];
        scanf("%d", &Cnt);
        for (int j = 1; j <= Cnt; ++j)
            scanf("%d", s_ + j);
        Topsort();
    }
}
int main() {
    scanf("%*d");
    while (~scanf("%d%d", &m, &n))
        Solve();
    return 0;
}

D. 星际旅行

题意

给定一个半径为r rr的n nn维球体和m mm个n nn维点。
求每个点到剩下m − 1 m-1m−1个点的不穿过球体的最短距离之和。
2 ≤ n ≤ 100 , 2 ≤ m ≤ 2000 , 1 ≤ r ≤ 1 0 3 , 0 ≤ ∣ x ∣ , ∣ y ∣ ≤ 1 0 3 2\le n\le100,2\le m\le2000,1\le r\le10^3,0\le |x|,|y|\le10^32≤n≤100,2≤m≤2000,1≤r≤103,0≤∣x∣,∣y∣≤103

题解

考虑二维的情况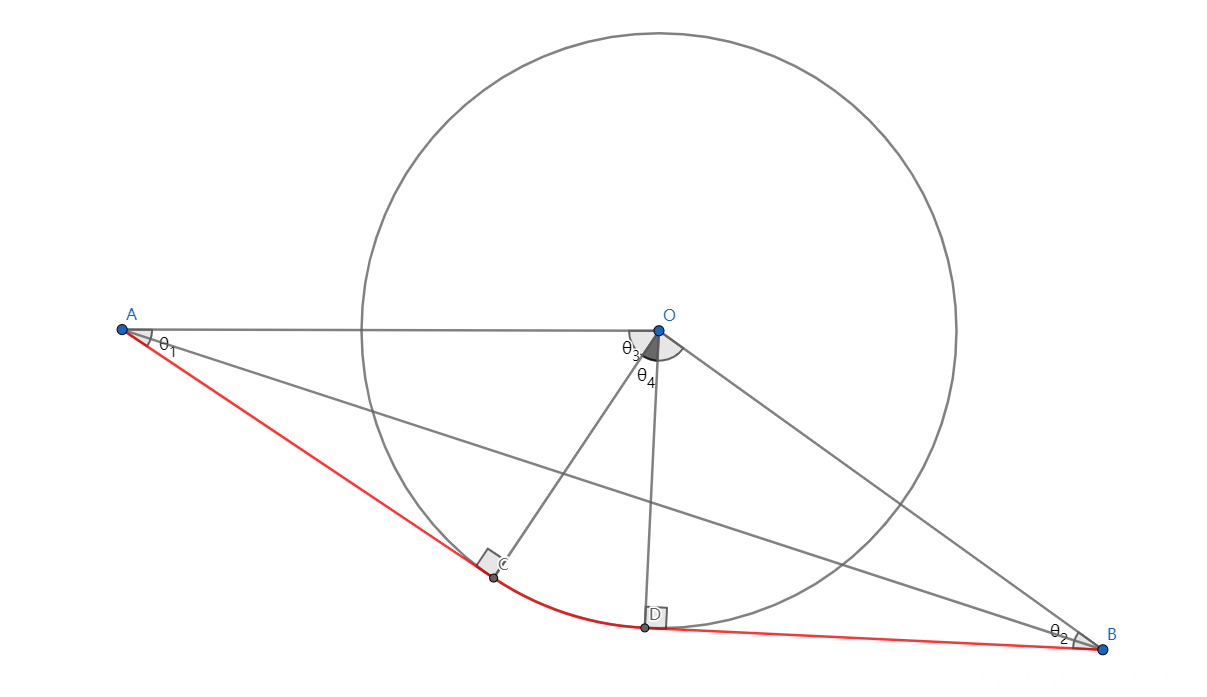
在这里插入图片描述
其中
θ 1 = ∠ O A C = arcsin ⁡ r ∣ A O ∣ θ 2 = ∠ O B D = arcsin ⁡ r ∣ B O ∣ θ 3 = ∠ A O B = arccos ⁡ ∣ A O ∣ 2 + ∣ B O ∣ 2 − ∣ A B ∣ 2 2 ∣ A O ∣ ∣ B O ∣ θ 4 = ∠ C O D = θ 3 − ( π 2 − θ 1 ) − ( π 2 − θ 2 ) = θ 1 + θ 2 + θ 3 − π \begin{aligned} \theta_1&=\angle OAC=\arcsin\frac{r}{|AO|}\\ \theta_2&=\angle OBD=\arcsin\frac{r}{|BO|}\\ \theta_3&=\angle AOB=\arccos\frac{|AO|^2+|BO|^2-|AB|^2}{2|AO||BO|}\\ \theta_4&=\angle COD=\theta_3-(\frac{\pi}2-\theta_1)-(\frac{\pi}2-\theta_2)=\theta_1+\theta_2+\theta_3-\pi \end{aligned}θ1​θ2​θ3​θ4​​=∠OAC=arcsin∣AO∣r​=∠OBD=arcsin∣BO∣r​=∠AOB=arccos2∣AO∣∣BO∣∣AO∣2+∣BO∣2−∣AB∣2​=∠COD=θ3​−(2π​−θ1​)−(2π​−θ2​)=θ1​+θ2​+θ3​−π​

则d i s ( A , B ) = A C ‾ + C D ⌢ + B D ‾ = ∣ A O ∣ 2 − r 2 + ∣ B O ∣ 2 − r 2 + r θ 4 dis(A,B)=\overline{AC}+\overset{\large\frown}{CD}+\overline{BD}=\sqrt{|AO|^2-r^2}+\sqrt{|BO|^2-r^2}+r\theta_4dis(A,B)=AC+CD⌢+BD=∣AO∣2−r2​+∣BO∣2−r2​+rθ4​.
当线段A B ABAB与圆不相交时，依照上式计算出来的θ 4 < 0 \theta_4<0θ4​<0，判断一下即可。
注意常数，时间复杂度O ( n m 2 ) O(nm^2)O(nm2)

#include <bits/stdc++.h>
using namespace std;
const int N = 100 + 5, M = 2e3 + 5;
const double Pi = acos(-1);
int n, m, r, r2;
double dis[M][M];
struct Point {
    int a[N];
    inline void init() {
        for (int i = 1; i <= n; ++i)
            scanf("%d", a + i);
    }
} O, p[M];
#define sqr(x) ((x) * (x))
inline int Len(Point a, Point b) {
    int L = 0;
    for (int i = 1; i <= n; ++i)
        L += sqr(a.a[i] - b.a[i]);
    return L;
}
int main() {
    scanf("%d%d%d", &n, &m, &r);
    O.init();
    r2 = r * r;
    for (int i = 1; i <= m; ++i)
        p[i].init();
    for (int i = 1; i <= m; ++i)
        for (int j = i + 1; j <= m; ++j) {
            double AO2 = Len(p[i], O), BO2 = Len(p[j], O), AB2 = Len(p[i], p[j]),
				   t1 = asin(r / sqrt(AO2)), t2 = asin(r / sqrt(BO2)),
                   t3 = acos((AO2 + BO2 - AB2) / (2 * sqrt(AO2 * BO2))),
                   t4 = t1 + t2 + t3 - Pi;
            if (t4 < 0)
                dis[i][j] = dis[j][i] = sqrt(AB2);
            else
                dis[i][j] = dis[j][i] = sqrt(AO2 - r2) + sqrt(BO2 - r2) + r * t4;
        }
    for (int i = 1; i <= m; ++i)
        printf("%.10lf\n", accumulate(dis[i] + 1, dis[i] + m + 1, 0.0));
    return 0;
}

E. 密信与计数

简要题意

给你一个解码本和一堆单词。
求长度为k的密文：不包含单词为子串，且解密后的明文是由单词组成的。这样的字符串有多少种。
在这里插入图片描述

题解

大佬的口糊题解：

解码本一页很简单
n页就多记一维状态就好了
考虑一页的情况
先把字典翻译回去
得到不超过38个的密文串
对字典建ac自动机
对于ac自动机上每个节点
我们dp
如果走到终止节点就不转移
版权声明：本文为BeNoble_原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接和本声明。