题面

题目描述

共有 4 种硬币。面值分别为 $c_{1}$ , $c_{2}$ , $c_{3}$ , $c_{4}$ 。

某人去商店买东西，去了 n 次，对于每次购买，他带了 $d{_i}$ 枚 i 种硬币，想购买 s的价值的东西。请问每次有多少种付款方法。

输入格式

输入的第一行是五个整数，分别代表 $c{_1}$ , $c{_2}$ , $c{_3}$ , $c{_4}$ , n。

接下来 n 行，每行有五个整数，描述一次购买，分别代表 $d{_1}$ , $d{_2}$ , $d{_3}$ , $d{_4}$ ,s。

输出格式

对于每次购买，输出一行一个整数代表答案。

说明/提示

数据规模与约定

对于 100% 的数据，保证 1 ≤ $c{_i}$ , $d{_i}$ ,s≤105，1 ≤ n ≤1000。

分析

四种硬币各有价值，选不超过一定个数的组成方案。这不就是一道裸的背包吗？于是果断敲出代码

算法一——多重背包

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define N 100003
int v[5],T,c[5],s;
ll f[N];
int main(){
	for(int i=1;i<=4;i++) scanf("%d",&v[i]);
	scanf("%d",&T);
	while(T--){
		for(int i=1;i<=4;i++) scanf("%d",&c[i]);
		scanf("%d",&s);
		memset(f,0,sizeof f);
		f[0]=1;
		for(int i=1;i<=4;i++)
			for(int j=s;j>=v[i];j--)
				for(int k=1;k<=c[i];k++)
					if(j-k*v[i]>=0)
						f[j]+=f[j-k*v[i]];
		printf("%lld\n",f[s]);
	}
	return 0;
}

经过观察，我们发现，多重背包部分时间复杂度为 $\Theta \left ( n^{2} \right )$ ,而对于每次询问都要进行一次，显然TLE

突然，我们发现，如果没有硬币数量的限制那就多好啊？直接一个完全背包预处理，然后 $\Theta \left ( 1 \right )$ 输出就好了。

我们先考虑一个简单一点的情况：只有第一个硬币有限制。

如果我们先完全背包预处理好无限制的情况，拿f[tot]减去f[tot-c[i]*(d[i]+1)]就是我们所需的合法方案数。

其实我们可以这样想，无限制的情况就是没有 $d{_i}$ ，而有限制时，这里的方案数包含了一部分超过d[i]个的。此时，我们将

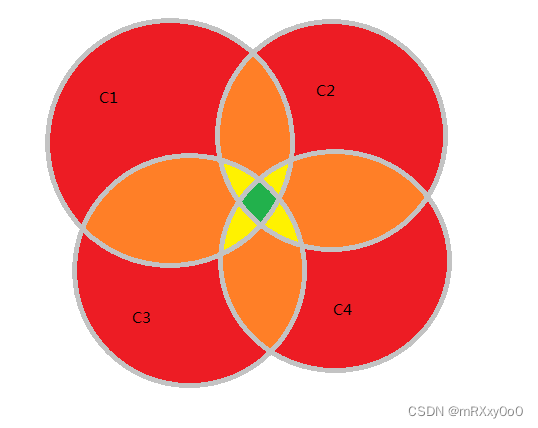
那么对于4个（或更多）的硬币有限制，我们就逐一把4个硬币单独限制的方案数减掉，这时可能会减重了（即同时两个硬币有限制的情况减了两次），所以我们再把4个硬币两两同时限制的方案数加上，可能又加重了，再把4个硬币33同时限制减掉，最后加上4个同时限制的方案数就是我们所需的答案。即容斥原理。

算法二——容斥原理+完全背包

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define N 100003
int c[5],T,d[5],s;
ll f[N],ans;
int F(int num){
	return c[num]*(d[num]+1);
}
int main(){
	for(int i=1;i<=4;i++) scanf("%d",&c[i]);
	scanf("%d",&T);
	f[0]=1;
	for(int i=1;i<=4;i++)
		for(int j=c[i];j<N;j++)
			f[j]+=f[j-c[i]];
	while(T--){
		for(int i=1;i<=4;i++) scanf("%d",&d[i]);
		scanf("%d",&s);
		ans=f[s];
		for(int i1=1;i1<=4;i1++){
			int t1=F(i1);
			if(s>=t1) ans-=f[s-t1];
			for(int i2=i1+1;i2<=4;i2++){
				int t2=F(i1)+F(i2);
				if(s>=t2) ans+=f[s-t2];
				for(int i3=i2+1;i3<=4;i3++){
					int t3=F(i1)+F(i2)+F(i3);
					if(s>=t3) ans-=f[s-t3];
					for(int i4=i3+1;i4<=4;i4++){
						int t4=F(i1)+F(i2)+F(i3)+F(i4);
						if(s>=t4) ans+=f[s-t4];
					}
				}
			}
		}
		printf("%lld\n",ans);
	}
	return 0;
}

显然，我们发现，中间部分实在是太复杂了，有什么方法可以帮助我们方便快捷地枚举所有情况呢？

二进制数

一个四个数的组合，可以用0000~1111表示，于是，我们对代码进行小小的优化——

算法二优化——二进制枚举

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define N 100003
int c[5],T,d[5],s;
ll f[N],ans;
int F(int num){
	return c[num]*(d[num]+1);
}
int main(){
	for(int i=1;i<=4;i++) scanf("%d",&c[i]);
	scanf("%d",&T);
	f[0]=1;
	for(int i=1;i<=4;i++)
		for(int j=c[i];j<N;j++)
			f[j]+=f[j-c[i]];
	while(T--){
		for(int i=1;i<=4;i++) scanf("%d",&d[i]);
		scanf("%d",&s);
		ans=f[s];
		for(int i=1;i<=15;i++){
			int cnt=s,k=0;
			for(int tmp=i,j=1;tmp;tmp>>=1,j++)
				if(tmp&1) k^=1,cnt-=F(j);
			if(cnt>=0) k?ans-=f[cnt]:ans+=f[cnt];
		}
		printf("%lld\n",ans);
	}
	return 0;
}

OK，成功AC

原文链接：https://blog.csdn.net/mRXxy0o0/article/details/127015775