补码表示的浮点数范围（详细解法）

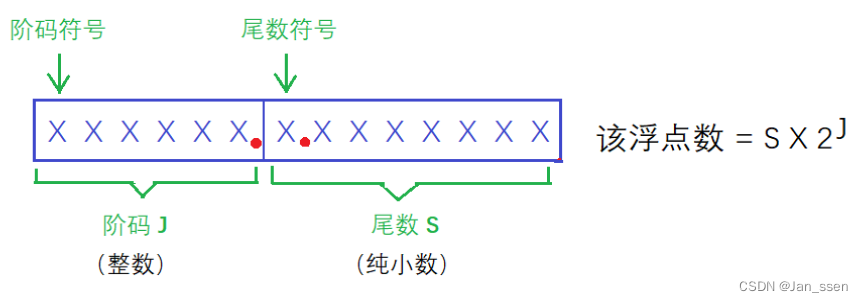
浮点数将整个字长分为两部分，其中一部分表示尾数，另一部分表示阶码。

         则浮点数所表示的数值大小为：尾数×2阶码

例如求该图所表示的浮点数

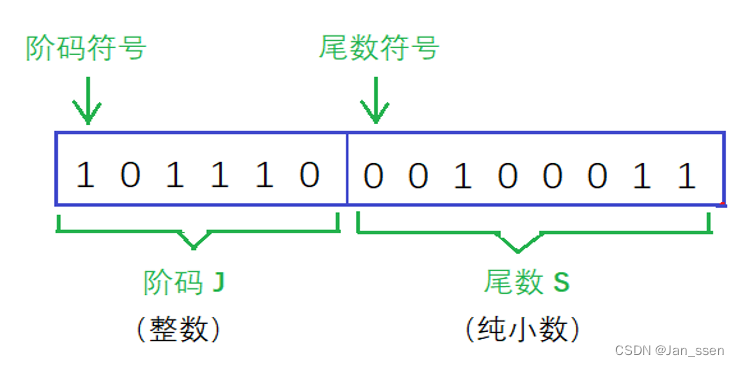
 对于阶码：101110为补码，符号位不变取反加一为110010 = -18

对于尾数：00100011原反补相同 = 

所以表示的浮点数为：（）* 

其次，我们要知道n位阶码和m位尾数的取值范围：

 对于n位二进制整数，取值范围为：

而对于n位小数，其实就是整数的小数点向前移动了n-1位，而由移位计算可知，左移一位=除2，所以取值范围其实就是n位二进制整数  ÷  = 

最后，就可以求浮点数对应的表示范围了

例：某浮点数字长共14位，其中尾数占8位（含符号位），阶码占6位（含符号位），尾数和阶码均采用补码表示，请写出该浮点数对应的表数范围

尾数范围： 

阶码范围：

综上，浮点数表示范围为：