时间、空间复杂度

时间复杂度

时间复杂度:算法中的基本操作的执行次数（那么算法是什么？）
算法：一系列的计算步骤；用来将输入的数据转化成输出结果
三条计算规则：（使用大O表示）
1；常数则取1。O(10)——>O(1);
2；只保留最高阶项。O(n ^ 2+2*n )——>O(n ^ 2 ) ;
3；最高阶项相乘的常数不是1；则除去这个常数。O(2n^2)——>O(n ^2);

想要得出一个算法的时间复杂度不能光看代码；还得具体结合思想。如果n是随机；比如一个算法查找内容复杂度可能是O（n），有可能是O（1）；这种情况我们都是指最好复杂度情况。

事例

二分查找时间复杂度分析：
如果光看二分查找的代码；很容易误认为是循环O（n）。假设最坏情况；到最后一次查找到；2^x=n 。(这里n是元素个数，x是执行次数)；每查一次砍掉一半数据；直到砍剩下最后一个找到。x=logn。我们复杂度里log默认是以2为底。

递归的时间复杂度：递归的次数*递归后执行的次数

斐波那契递归时间复杂度：形如一颗二叉树。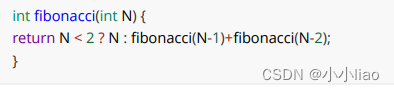

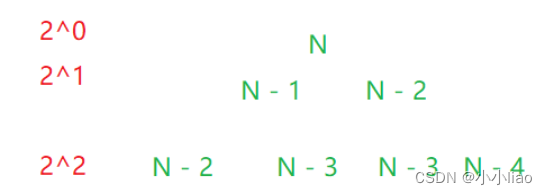
递归次数是多少：2^0+……2 ^(n-1) 递归后的执行次数是多少 ：2
我们这里计算的结果会缺少一部分；有些N会先执行到1就结束；不影响结果；因为是粗略的时间复杂度。

如果是使用循环的写法：时间复杂度是O（n）；递归的速度求此结果是比较慢的

空间复杂度

空间复杂度：衡量一个算法浪费内存的情况；临时空间。
以下代码的空间复杂度为O（1）；因为途中并没有因为输入的数据增大而创建更大的空间

void bubbleSort(int[] array) {
//假设我在循环里添加int[ ]tmp=new int[array.length];
for (int end = array.length; end > 0; end--) {
		boolean sorted = true;//这里的循环定义；第二次循环；第一次的都被回收掉了。（没有随着n变多；而临时变量增加）
		for (int i = 1; i < end; i++) {
			if (array[i - 1] > array[i]) {
				Swap(array, i - 1, i);
				sorted = false;
				}
			}
		
		if (sorted == true) {
					break;
		}
	}

斐波那契空间复杂度:此代码和上方类似；

这里空间浪费在每调用一次就在栈上开辟一份空间；随N的增大；开辟的空间越大。因为这里是递归；归得在最后；如果是循环就可以一边回收一边创建。。O（n）

比如N=3；这里非常奇妙。只有左边归还之后（空间回收）；右边才会继续执行开辟空间。又因为左边是N-1；右边是N-2；刚刚好回收的空间就与要开辟的右边是一样的。所以这里最多就需要开辟出N个空间。O(N)