1. 题目

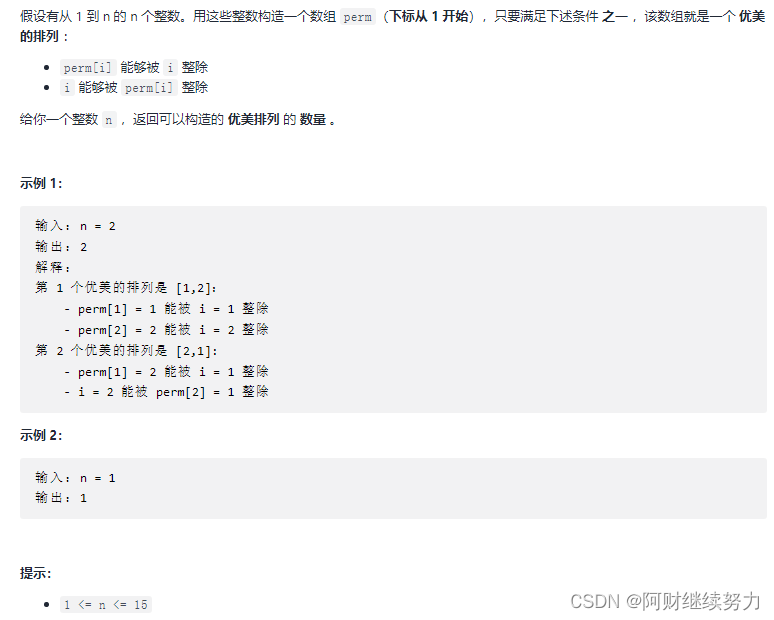
2. 思路

(1) 回溯法

• 初始时，arr[i]=i，对于下标i，arr[i]与后面的元素交换位置即可得到n个数的全排列，每次交换时判断是否符合条件，符合则交换。

(2) 状态压缩+动态规划

• 由于n<=15，因此，可以利用一个位数为n的二进制数mask表示排列中的数被选取的情况，若第i位为1，则表示i+1被选取；若第i位为0，则表示i+1未被选取。
• 当计算dp[mask]时，只需要在前num(mask)−1位都已经放置了数的情况下，考虑第num(mask)位要放置的数即可，枚举当前位符合条件的数，并将方案数累加到dp[mask]中即可。

3. 代码

public class Test {
    public static void main(String[] args) {
    }
}

class Solution {
    public int n;
    public int[] arr;
    public int res;

    public int countArrangement(int n) {
        this.n = n;
        arr = new int[n + 1];
        res = 0;
        for (int i = 1; i <= n; i++) {
            arr[i] = i;
        }
        backtrack(1);
        return res;
    }

    public void backtrack(int index) {
        if (index == n + 1) {
            res++;
            return;
        }
        int num = arr[index];
        for (int i = index; i <= n; i++) {
            if (arr[i] % index == 0 || index % arr[i] == 0) {
                arr[index] = arr[i];
                arr[i] = num;
                backtrack(index + 1);
                arr[i] = arr[index];
                arr[index] = num;
            }
        }
    }
}

class Solution1 {
    public int countArrangement(int n) {
        int[] dp = new int[1 << n];
        dp[0] = 1;
        for (int mask = 1; mask < (1 << n); mask++) {
            int num = Integer.bitCount(mask);
            for (int i = 0; i < n; i++) {
                if ((mask & (1 << i)) != 0 && ((num % (i + 1)) == 0 || (i + 1) % num == 0)) {
                    dp[mask] += dp[mask ^ (1 << i)];
                }
            }
        }
        return dp[(1 << n) - 1];
    }
}