
本文参考下链 ,如果对数据集或书内更多更多讲解内容感兴趣,请直接购买
智能风控(原理,算法与工程实践)www.amazon.cn这篇手码了一遍梅子行在书中的递归筛选方案,梳理的框架上是这样的.
- 首先定义了在风控场景下,特征迭代筛选和两个关键性指标:
- KS:模型的正负样本体现的关键指标,这与普通学习任务中的针对AUC,Precision等的优化方向不一样,所以基本自己定义了一个评价指标。
- PSI:模型各个在各个检测分段上的检测稳定性.
也就是区分能力要强,模型结果要稳定.
需要注意的是,我们在使用XGBoost的时候其实有自带一个Featureimportance功能(上一篇写xgboost有提到,分为weight, gain和cover三种不同形式),如果我们在入模之前没有对模型特征做相关性的处理的话,直接使用XGBoost进行特征筛选是不合理的. 我下面举个例子:
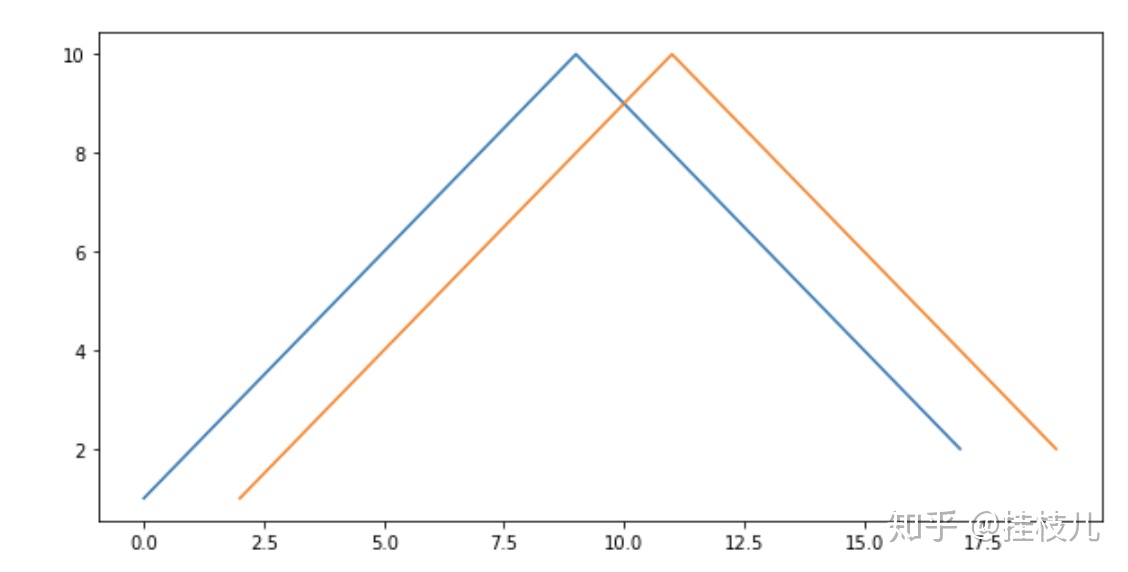
如果有两个特征的分布是像上图这样的,可以发现他们的相关性一定是差不多的,在XGBOOST用于分裂时2个特征肯定会被随机用来分树,那么这两个本身如果重要性比较高的话,特征的真正重要性就会丢失。
回到书中的内容,这节先定义了2个评估模型效果的函数
SolveKS:
用于计算当前模型在某数据集上的KS,KS值对模型的评价不会受到样本不均衡问题的影响.
这些函数都继承自之前XGBoost父类
注意这个函数还加了个Weight参数,这是为了还原真实样本比例下的比例,举个例子,正样本有100,负样本有10000,对负样本按照0.4的比例进行下采样,就会得到4000的负样本,对100的正样本和4000的负样本进行建模,但是需要将负样本的权重设置为2.5,才能还原到初始的正负样本的比例
def sloveKS(self, model, X, Y, Weight):
Y_predict = [s[1] for s in model.predict_proba(X)]
nrows = X.shape[0]
#还原权重
lis = [(Y_predict[i], Y.values[i], Weight[i]) for i in range(nrows)]
#按照预测概率倒序排列
ks_lis = sorted(lis, key=lambda x: x[0], reverse=True)
KS = list()
bad = sum([w for (p, y, w) in ks_lis if y > 0.5])
good = sum([w for (p, y, w) in ks_lis if y <= 0.5])
bad_cnt, good_cnt = 0, 0
for (p, y, w) in ks_lis:
if y > 0.5:
#1*w 即加权样本个数
bad_cnt += w
else:
#1*w 即加权样本个数
good_cnt += w
ks = math.fabs((bad_cnt/bad)-(good_cnt/good))
KS.append(ks)
return max(KS)
solvePSI
这个指标可以比较好的衡量模型或特征的稳定性,可以用于监控线上模型和线下的差异.
def slovePSI(self, model, dev_x, val_x):
dev_predict_y = [s[1] for s in model.predict_proba(dev_x)]
dev_nrows = dev_x.shape[0]
dev_predict_y.sort()
#等频分箱成10份
cutpoint = [100] + [dev_predict_y[int(dev_nrows/10*i)]
for i in range(1, 10)] + [100]
cutpoint = list(set(cutpoint))
cutpoint.sort()
val_predict_y = [s[1] for s in list(model.predict_proba(val_x))]
val_nrows = val_x.shape[0]
PSI = 0
#每一箱之间分别计算PSI
for i in range(len(cutpoint)-1):
start_point, end_point = cutpoint[i], cutpoint[i+1]
dev_cnt = [p for p in dev_predict_y
if start_point <= p < end_point]
dev_ratio = len(dev_cnt) / dev_nrows + 1e-10
val_cnt = [p for p in val_predict_y
if start_point <= p < end_point]
val_ratio = len(val_cnt) / val_nrows + 1e-10
psi = (dev_ratio - val_ratio) * math.log(dev_ratio/val_ratio)
PSI += psi
return PSI 开始特征筛选.
这个函数我手码了一遍,用minscore来控制筛选的阈值,用maxdelvarnums来控制每次删除特征的个数,同时输出每一轮筛选后对应模型ks和psi指标的变化,真的很夯啊。另外我之前分析kaggle数据的时候一般会通过woe和iv组合来计算特征的有效性,但书中也提到了,这个指标是针对单变量的特征效果,XGBoost本身是有特征交叉能力的,所以如果用IV 来分析的话,只可以用来做特征的粗筛选.
import xgboost as xgb
from xgboost import plot_importance
class xgBoost(object):
def __init__(self, datasets, uid, dep, weight,
var_names, params, max_del_var_nums=0):
self.datasets = datasets
#样本唯一标识,不参与建模
self.uid = uid
#二分类标签
self.dep = dep
#样本权重
self.weight = weight
#特征列表
self.var_names = var_names
#参数字典,未指定字段使用默认值
self.params = params
#单次迭代最多删除特征的个数
self.max_del_var_nums = max_del_var_nums
self.row_num = 0
self.col_num = 0
def training(self, min_score=0.0001, modelfile="", output_scores=list()):
lis = self.var_names[:]
dev_data = self.datasets.get("dev", "") #训练集
val_data = self.datasets.get("val", "") #测试集
off_data = self.datasets.get("off", "") #跨时间验证集
#从字典中查找参数值,没有则使用第二项作为默认值
model = xgb.XGBClassifier(
learning_rate=self.params.get("learning_rate", 0.1),
n_estimators=self.params.get("n_estimators", 100),
max_depth=self.params.get("max_depth", 3),
min_child_weight=self.params.get("min_child_weight", 1),subsample=self.params.get("subsample", 1),
objective=self.params.get("objective",
"binary:logistic"),
nthread=self.params.get("nthread", 10),
scale_pos_weight=self.params.get("scale_pos_weight", 1),
random_state=0,
n_jobs=self.params.get("n_jobs", 10),
reg_lambda=self.params.get("reg_lambda", 1),
missing=self.params.get("missing", None) )
while len(lis) > 0:
#模型训练
model.fit(X=dev_data[self.var_names], y=dev_data[self.dep])
#得到特征重要性
scores = model.feature_importances_
#清空字典
lis.clear()
'''
当特征重要性小于预设值时,
将特征放入待删除列表。
当列表长度超过预设最大值时,跳出循环。
即一次只删除限定个数的特征。
'''
for (idx, var_name) in enumerate(self.var_names):
#小于特征重要性预设值则放入列表
if scores[idx] < min_score:
lis.append(var_name)
#达到预设单次最大特征删除个数则停止本次循环
if len(lis) >= self.max_del_var_nums:
break
#训练集KS
devks = self.sloveKS(model, dev_data[self.var_names],
dev_data[self.dep], dev_data[self.weight])
#初始化ks值和PSI
valks, offks, valpsi, offpsi = 0.0, 0.0, 0.0, 0.0
#测试集KS和PSI
if not isinstance(val_data, str):
valks = self.sloveKS(model,
val_data[self.var_names],
val_data[self.dep],
val_data[self.weight])
valpsi = self.slovePSI(model,
dev_data[self.var_names],
val_data[self.var_names])
#跨时间验证集KS和PSI
if not isinstance(off_data, str):
offks = self.sloveKS(model,
off_data[self.var_names],
off_data[self.dep],
off_data[self.weight])
offpsi = self.slovePSI(model,
dev_data[self.var_names],
off_data[self.var_names])
#将三个数据集的KS和PSI放入字典
dic = {"devks": float(devks),
"valks": float(valks),
"offks": offks,
"valpsi": float(valpsi),
"offpsi": offpsi}
print("del var: ", len(self.var_names),
"-->", len(self.var_names) - len(lis),
"ks: ", dic, ",".join(lis))
plot_importance(model)
#重新训练,准备进入下一循环
model = xgb.XGBClassifier(
learning_rate=self.params.get("learning_rate", 0.1),
n_estimators=self.params.get("n_estimators", 100),
max_depth=self.params.get("max_depth", 3),
min_child_weight=self.params.get("min_child_weight",1),
subsample=self.params.get("subsample", 1),
objective=self.params.get("objective",
"binary:logistic"),
nthread=self.params.get("nthread", 10),
scale_pos_weight=self.params.get("scale_pos_weight",1),
random_state=0,
n_jobs=self.params.get("n_jobs", 10),
reg_lambda=self.params.get("reg_lambda", 1),
missing=self.params.get("missing", None)) 版权声明:本文为weixin_34722015原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。