欧拉角与四元数之间的相互转换

欧拉角到四元数

将旋转分为三次，方向分别为[1, 0, 0]，[0, 1, 0]与[0, 0, 1]，角度为α，β与γ，则相对应的四元数分别如下所示

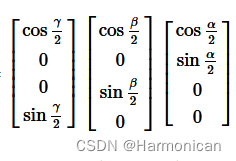
将三个四元数相乘可得到坐标经过三次旋转之后所得到的位置四元数表示形式，具体如下

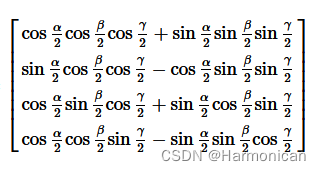
则从欧拉角到四元数转换所对应形式如上所示。

MATLAB实现代码如下

function quat = euler2quat(phi, theta, psi)
    quat = [cos(psi/2) * cos(theta/2) * cos(phi/2) + sin(psi/2) * sin(theta/2) * sin(phi/2);
           (cos(psi/2) * cos(theta/2) * sin(phi/2) - sin(psi/2) * sin(theta/2) * cos(phi/2)) * 1i;
           (cos(psi/2) * sin(theta/2) * cos(phi/2) + sin(psi/2) * cos(theta/2) * sin(phi/2)) * 1i;
           (sin(psi/2) * cos(theta/2) * cos(phi/2) - cos(psi/2) * sin(theta/2) * sin(phi/2)) * 1i];
end

 四元数到欧拉角

欧拉角形式下坐标旋转矩阵如下

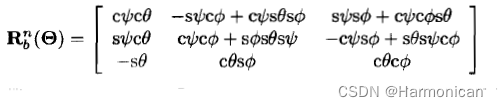
四元数形式下坐标旋转矩阵如下

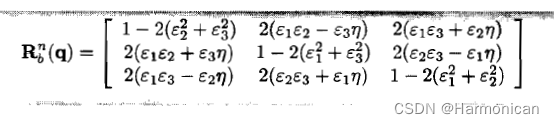
将两个形式进行对应，可得到

MATLAB代码实现如下

function [phi, theta, psi] = quat2euler(quat)
    Ita = quat(1);
    eps1 = imag(quat(2));
    eps2 = imag(quat(3));
    eps3 = imag(quat(4));
    
    phi = atan2(2 * (eps2 * eps3 + Ita * eps1), 1 - 2 * (eps1.^2 + eps2.^2));
%     phi = atan(2 * (eps2 * eps3 - Ita * eps1) / (1 - 2 * (eps1.^2 + eps2.^2)));
    theta = asin(2 * (Ita * eps2 - eps1 * eps3));
    psi = atan2(2 * (eps1 * eps2 + Ita * eps3), 1 - 2 * (eps2.^2 + eps3.^2));
%     psi = atan(2 * (eps1 * eps2 - Ita * eps3) / (1 - 2 * (eps2.^2 + eps3.^2)));
end

测试

先将指定四元数转换为欧拉角

quat = [0.9437; 0.1277i; -0.1449i; 0.2685i];

[phi, theta, psi] = quat2euler(quat);

结果如下

再将所生成欧拉角转换为四元数

quat1 = euler2quat(phi, theta, psi)

结果如下

 初始化四元数与转换生成四元数对比一致