1 最小二乘问题
目标函数为若干个函数的平方和的最优化问题:
其中,x∈Rn,m≥n,这类问题称为最小二乘问题。当每个ri(x)都是线性函数时,问题(7.5.1)称为线性最小二乘问题,否则称为非线性最小二乘问题。
2 线性最小二乘法

从而问题(7.5.1)可表示为:
由于f(x)是凸函数,因此: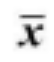
必是全局极小点。因此对于线性最小二乘问题,只要ATA非奇异,就可用式(7.5.4)求解。
3 非线性最小二乘法
设问题(7.5.1)中ri(x)是非线性函数,且f(x)存在连续偏导数,则问题(7.5.1)成为非线性最小二乘问题,因此不能利用式(7.5.4)求解。
下面介绍两种方法。
3.1 高斯-牛顿法


3.2 Levenberg-Marquardt方法
在高斯-牛顿法中,有时会出现J(x(k))TJ(x(k))奇异或接近奇异的情形,这时求解方程组(7.5.10)会遇到很大困难,甚至根本不能进行。因此人们提出了一些修正算法。
具体后续内容待补充。
4 参考书籍
《最优化理论与方法》-王景恒,北京:北京理工大学出版社,2018.8
END
版权声明:本文为qq_40061206原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。