算法学习记录-二叉树的权值

算法学习记录

二叉树的权值

真没想到想到,就这样一道题花了我一上午…

一开始思路比较乱,后来不停的开单步调试,不停的看各种值,不停的想思路和代码是不是一样的,调了一上午最后终于悟出来了.

刚开始的时候只是脑子里能想明白怎么求和, 但是不能写出具体流程就之间写代码了.

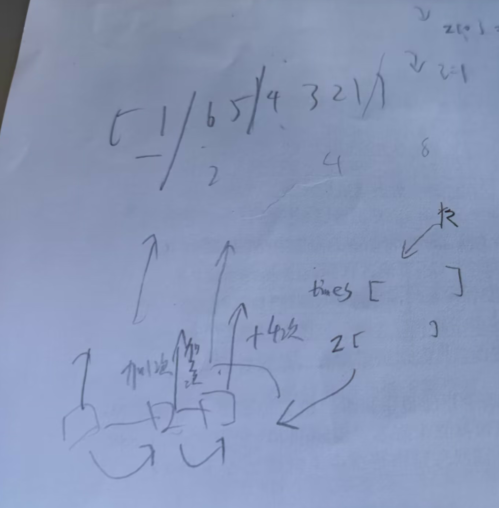
后来错了半天才画出来个这个,然后思路清晰明了了.

刚开始的时候容易搞混各种索引用的下标, 起名字都是xyz很抽象,后边改成这样就好了,

一开始错了一个小时想不通挺难受的,后来给chatgpt看,虽然它不能帮我写出正确的代码,但是帮我改了点名字,再加上画出了图,最后想通了. 思路不清晰的时候调试很难受, 甚至不知道该看哪些, 状态很混沌.

思路

因为是完全二叉树, 显然容易知道怎么算每一层 ,有1,2,4,8,16这样的,每下一层就是上一层的乘以2

自己手算是用斜线隔开, 开始一个个求和来算, 每个隔开的是1,2,4,8,每次求和都要求1,2,4,8这种,

因为c语言不太好表示这种算的方法, 再多一层抽象,

每个斜杠后边开始加多少次是一组要标记的状态, 记到一个数组times[]里,

求和也是一组状态, 求出的和也加到另一个数组里, 这两个数组应该是等长的.

求和应该按照times[]里的次数来, 加购了指定的次数就开始按照下一个的次数加(指针+1)

然后是边界,比如7这种可以看成是log(4)+1,这样比log(7+1)的好处在于如果他有一颗树正好比第二颗数多一层,也不会收到影响.

额,其实完全把大脑里的算法写道程序里也不是那么容易, 有时候为了适应用的编程语言要再多一层抽象, 不过这个过程能让逻辑变的特别清晰, 也不错.

代码

#include <stdio.h>
//#include <stdlib.h>
#include <math.h>
//void debug_print(int x){
//    printf("%d\n",x);
//}


int main(){
    int n;
    scanf("%d", &n);

    // 计算完全二叉树的深度
    int depth = (int)log2(n) + 1;
//    debug_print(depth);
    // 每一层加多少次
    int times[depth];
    int sum = 1;
    for (int i = 0; i < depth; i++) {
        times[i] = sum;
        sum *= 2;
//        debug_print(times[i]);
    }

    // 计算每一层节点的权值和
    int values[depth];
    for (int i = 0; i < depth; i++) {
        values[i] = 0;
    }

    int z_pointer=0,count=0;
    for (int i = 0; i < n; i++) {
        int val;
        if (scanf("%d", &val) != 1) {
            fprintf(stderr, "Error: invalid input format\n");
            return 1;
        }
        values[z_pointer] += val;
        if (count == times[z_pointer]) {
            count=0;
            z_pointer++;
        }else{
            count++;
        }
    }

    // 找出最大的权值和以及对应的深度
    int max = values[0];
    int min_depth = 0;
    for (int i = 1; i < depth; i++) {
        if (values[i] > max) {
            max = values[i];
            min_depth = i;
        }
    }

    // 输出结果
    printf("%d\n", min_depth + 1);
    return 0;
}

总结

虽然做的慢, 但还是想通了很多, 值. 而且这个算法复杂度在O(n), 效率很满意.