《剑指 Offer （第 2 版）》数组部分 JavaScript 题解

《剑指 Offer（第 2 版）》通行全球的程序员经典面试秘籍。剖析典型的编程面试题，系统整理基础知识、代码质量、解题思路、优化效率和综合能力这 5 个面试要点。

最近，把数组部分的题刷完了。本文来分享下这些题的解法

03. 数组中重复的数字

找出数组中重复的数字。

在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。

示例 1：

输入：
[2, 3, 1, 0, 2, 5, 3]
输出：2 或 3 

限制：

• 2 <= n <= 100000

题目地址：https://leetcode-cn.com/problems/shu-zu-zhong-zhong-fu-de-shu-zi-lcof/

解题思路

由于只需要找出数组中任意一个重复的数字，因此遍历数组，遇到重复的数字即返回。为了判断一个数字是否重复遇到，使用集合存储已经遇到的数字，如果遇到的一个数字已经在集合中，则当前的数字是重复数字。

/**
 * @param {number[]} nums
 * @return {number}
 */
var findRepeatNumber = function(nums) {
    const set = new Set();
    for(const num of nums) {
        if (set.has(num)) return num;
        set.add(num);
    }
};

04. 二维数组中的查找

在一个 n * m 的二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个高效的函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

示例:

现有矩阵 matrix 如下：

[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

给定 target = 5，返回 true。

给定 target = 20，返回 false。

限制：

• 0 <= n <= 1000
• 0 <= m <= 1000

题目地址：https://leetcode-cn.com/problems/er-wei-shu-zu-zhong-de-cha-zhao-lcof/

解题思路

若使用暴力法遍历矩阵 matrix ，则时间复杂度为 O(NM) 。暴力法未利用矩阵 “从上到下递增、从左到右递增” 的特点，显然不是最优解法。

如下图所示，我们将矩阵逆时针旋转 45° ，并将其转化为图形式，发现其类似于 二叉搜索树 ，即对于每个元素，其左分支元素更小、右分支元素更大。因此，通过从 “根节点” 开始搜索，遇到比 target 大的元素就向左，反之向右，即可找到目标值 target 。

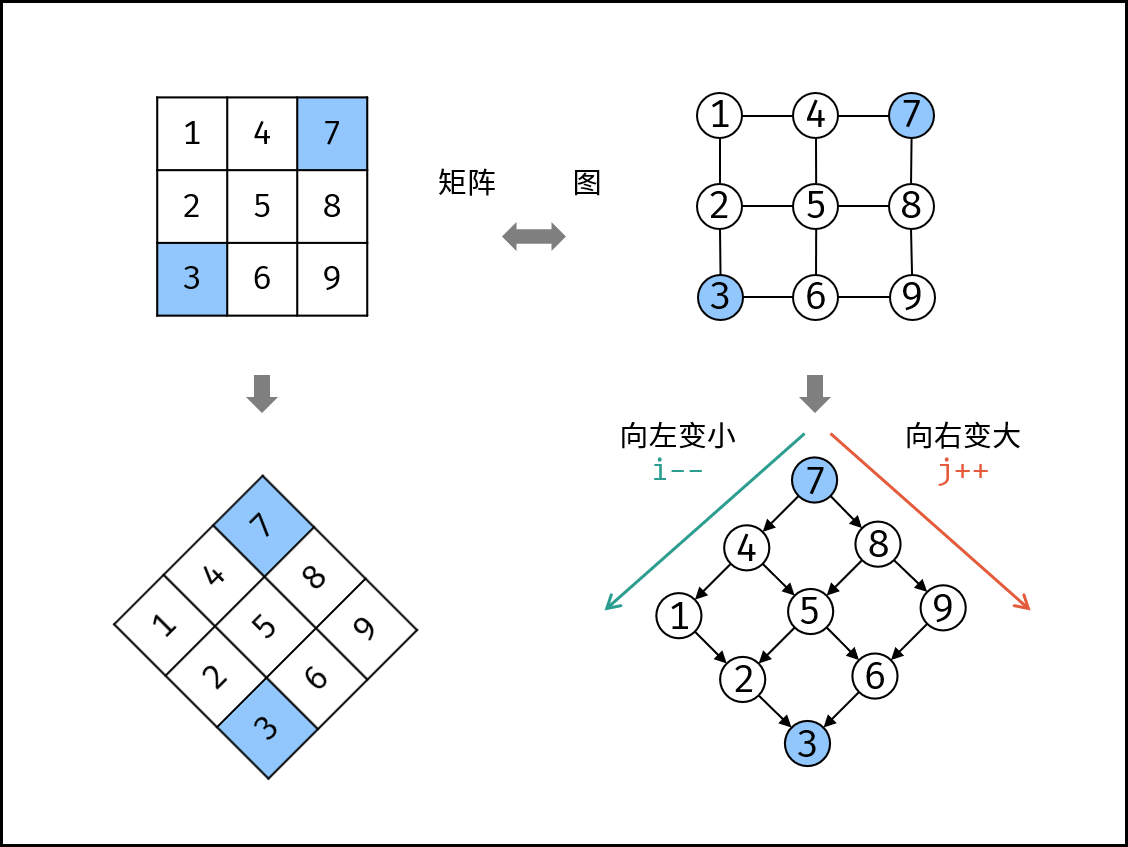
“根节点” 对应的是矩阵的 “左下角” 和 “右上角” 元素，本文称之为 标志数 ，以 matrix 中的 左下角元素 为标志数 flag ，则有:

• 若 flag > target ，则 target 一定在 flag 所在 行的上方 ，即 flag 所在行可被消去。
• 若 flag < target ，则 target 一定在 flag 所在 列的右方 ，即 flag 所在列可被消去。

算法流程：

1. 从矩阵 matrix 左下角元素（索引设为 (i, j) ）开始遍历，并与目标值对比：
   • 当 matrix[i][j] > target 时，执行 i-- ，即消去第 i 行元素；
   • 当 matrix[i][j] < target 时，执行 j++ ，即消去第 j 列元素；
   • 当 matrix[i][j] = target 时，返回 true ，代表找到目标值。
2. 若行索引或列索引越界，则代表矩阵中无目标值，返回 false 。

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var findNumberIn2DArray = function(matrix, target) {

    let [i, j] = [matrix.length - 1, 0];
    while(i >= 0 && j < matrix[0].length) {
        if (target > matrix[i][j]) {
            j++;
        } else if (target < matrix[i][j]) {
            i--;
        } else {
            return true;
        }
    }
    return false;
};

07. 重建二叉树

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例 1:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

限制：

• 0 <= 节点个数 <= 5000

题目地址：https://leetcode-cn.com/problems/zhong-jian-er-cha-shu-lcof/

解题思路

对于任意一颗树而言，前序遍历的形式总是

[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]
即根节点总是前序遍历中的第一个节点。而中序遍历的形式总是

[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]
只要我们在中序遍历中定位到根节点，那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的，因此我们就可以对应到前序遍历的结果中，对上述形式中的所有左右括号进行定位。

这样以来，我们就知道了左子树的前序遍历和中序遍历结果，以及右子树的前序遍历和中序遍历结果，我们就可以递归地对构造出左子树和右子树，再将这两颗子树接到根节点的左右位置。

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function(preorder, inorder) {
    if (preorder.length === 0) return null;
    if (preorder === 1) return new TreeNode(preorder[0]);
    function build(preorderStart, preorderEnd, inorderStart, inorderEnd) {
        const root = new TreeNode(preorder[preorderStart]);
        const rootIndex = inorder.indexOf(preorder[preorderStart]);
        root.left = rootIndex === inorderStart ? null : 
            build(preorderStart + 1, preorderStart + rootIndex - inorderStart, inorderStart, rootIndex - 1);
        root.right = rootIndex === inorderEnd ? null : 
            build(preorderStart + rootIndex - inorderStart + 1, preorderEnd, rootIndex + 1, inorderEnd);
        return root;
    }
    return build(0, preorder.length - 1, 0, inorder.length - 1);
};

11. 旋转数组的最小数字

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。

给你一个可能存在 重复 元素值的数组 numbers ，它原来是一个升序排列的数组，并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转，该数组的最小值为1。

示例 1：

输入：[3,4,5,1,2]
输出：1

示例 2：

输入：[2,2,2,0,1]
输出：0

题目地址：https://leetcode-cn.com/problems/xuan-zhuan-shu-zu-de-zui-xiao-shu-zi-lcof/

解题思路

一个包含重复元素的升序数组在经过旋转之后，可以得到下面可视化的折线图：

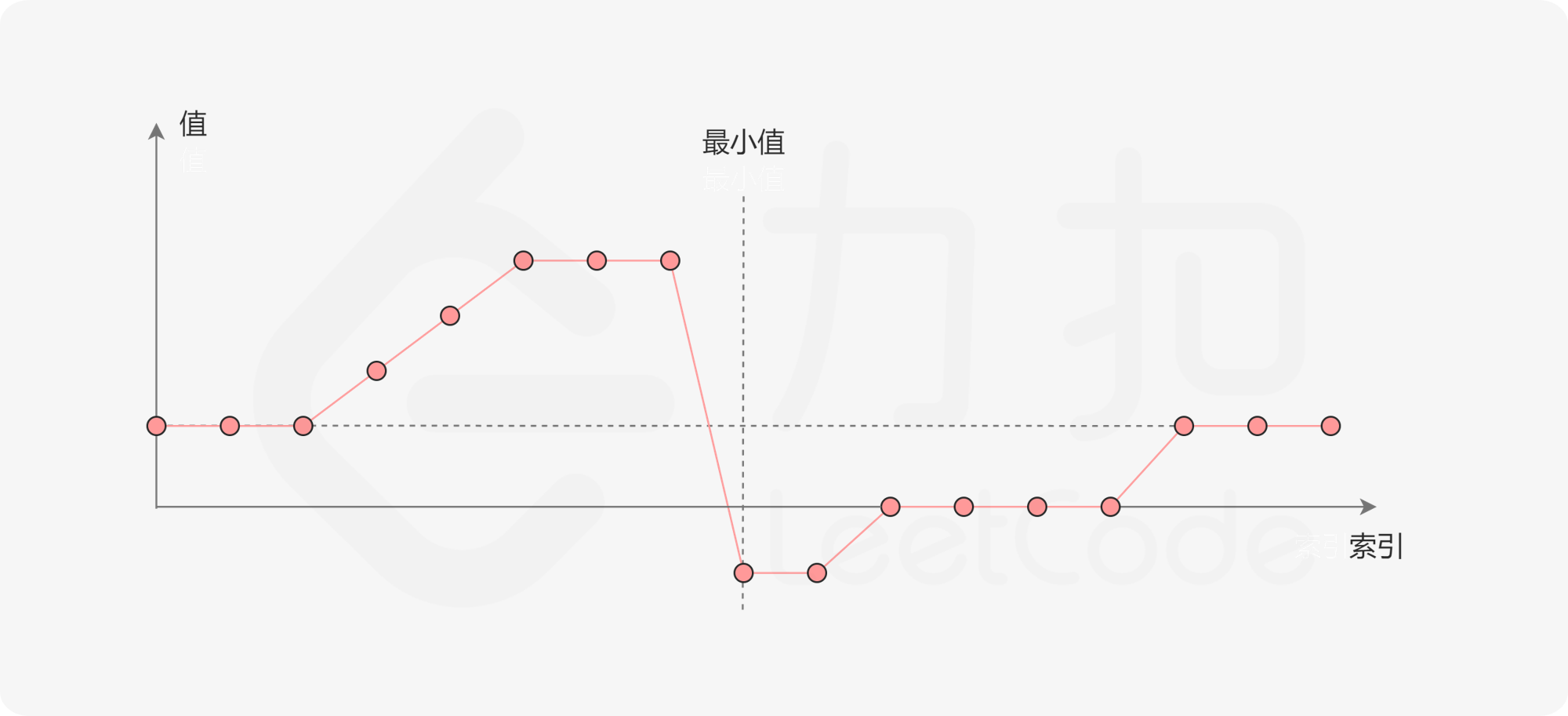
其中横轴表示数组元素的下标，纵轴表示数组元素的值。图中标出了最小值的位置，是我们需要查找的目标。

我们考虑数组中的最后一个元素 x：在最小值右侧的元素，它们的值一定都小于等于 x；而在最小值左侧的元素，它们的值一定都大于等于 x。因此，我们可以根据这一条性质，通过二分查找的方法找出最小值。

在二分查找的每一步中，左边界为 low，右边界为 high，区间的中点为 pivot，最小值就在该区间内。我们将中轴元素 numbers[pivot] 与右边界元素 numbers[high] 进行比较，可能会有以下的三种情况：

第一种情况是 numbers[pivot]<numbers[high]。如下图所示，这说明 numbers[pivot] 是最小值右侧的元素，因此我们可以忽略二分查找区间的右半部分。

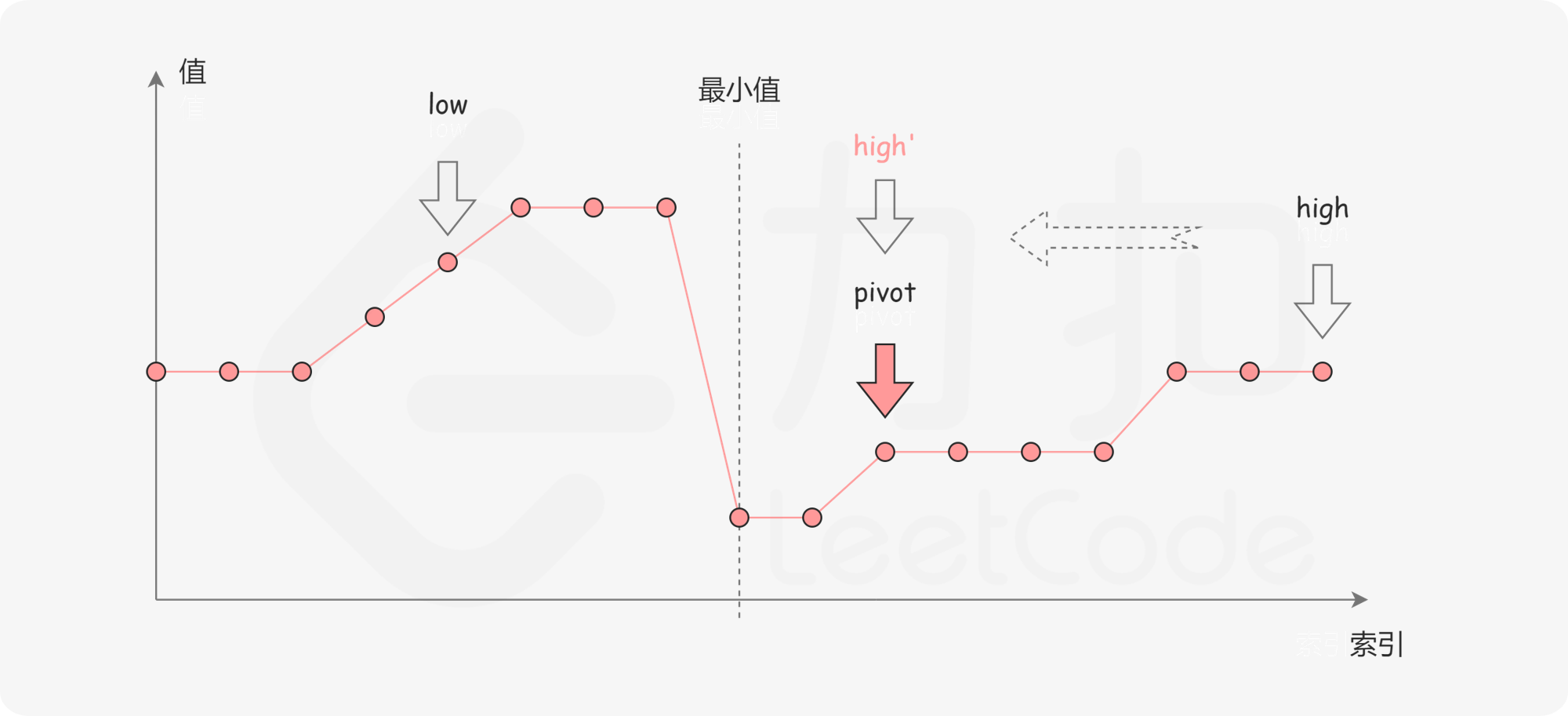
第二种情况是 numbers[pivot]>numbers[high]。如下图所示，这说明 numbers[pivot] 是最小值左侧的元素，因此我们可以忽略二分查找区间的左半部分。

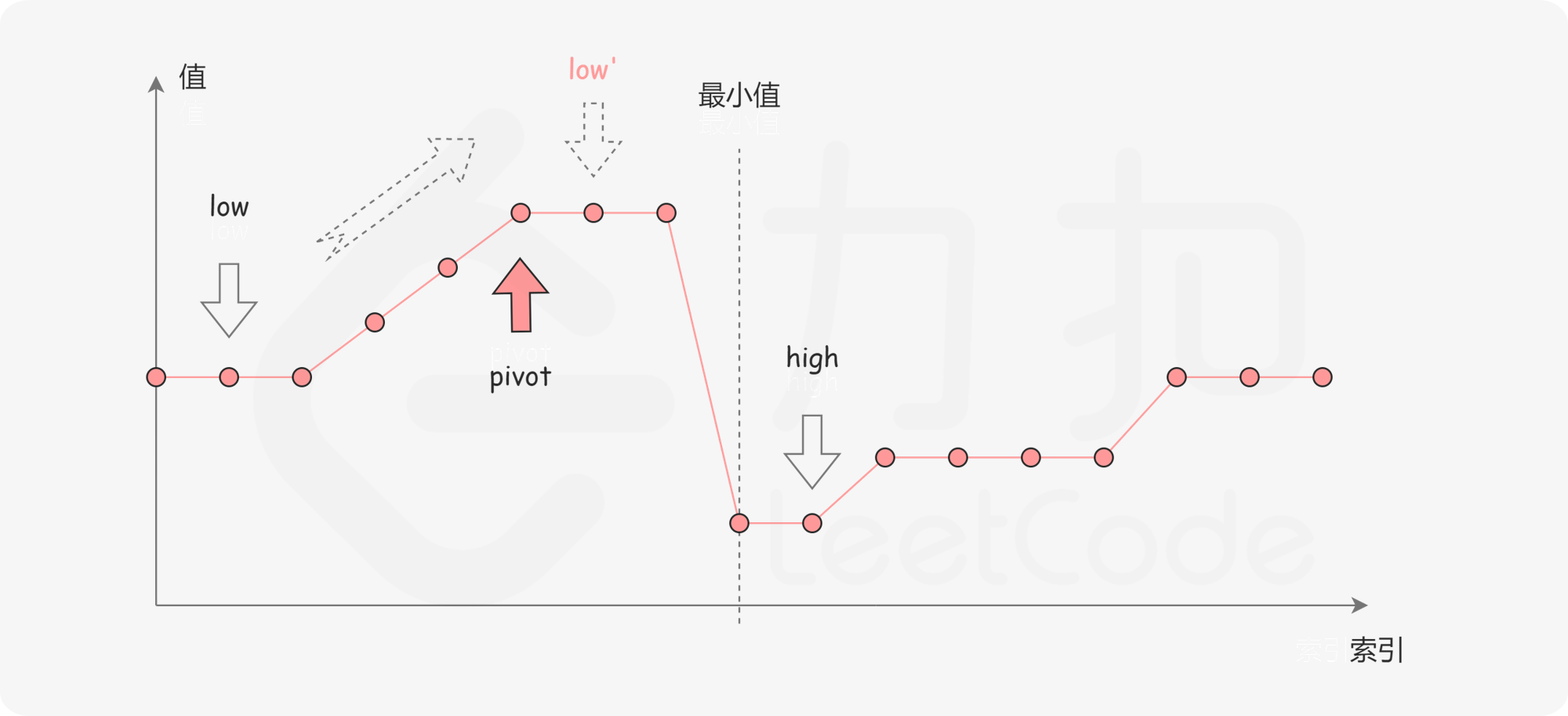
第三种情况是 numbers[pivot]==numbers[high]。如下图所示，由于重复元素的存在，我们并不能确定 numbers[pivot] 究竟在最小值的左侧还是右侧，因此我们不能莽撞地忽略某一部分的元素。我们唯一可以知道的是，由于它们的值相同，所以无论 numbers[high] 是不是最小值，都有一个它的「替代品」numbers[pivot]，因此我们可以忽略二分查找区间的右端点。

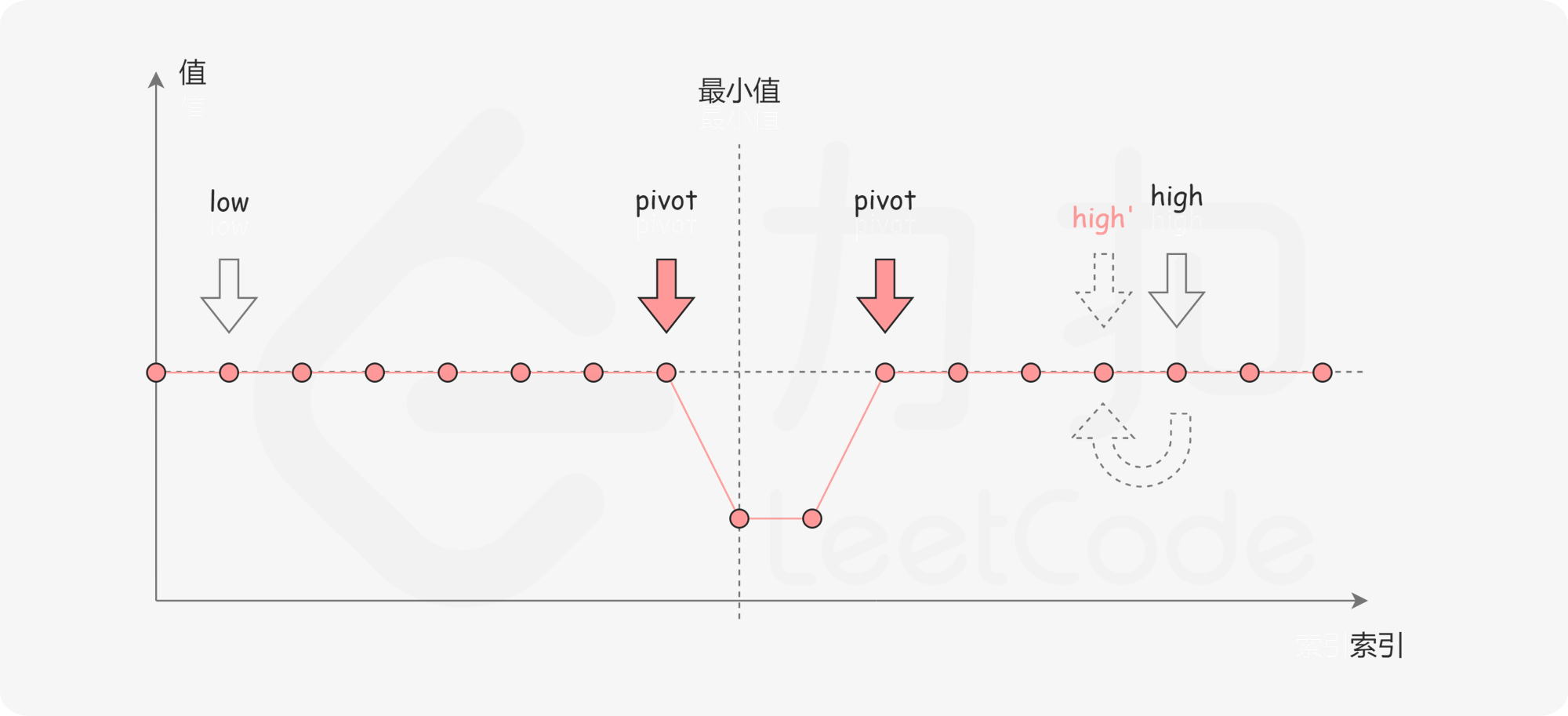
当二分查找结束时，我们就得到了最小值所在的位置。

/**
 * @param {number[]} numbers
 * @return {number}
 */
var minArray = function(numbers) {
    let [low, high] = [0, numbers.length - 1];
    while (low < high) {
        const pivot = low + Math.floor((high - low) / 2);
        if (numbers[pivot] < numbers[high]) {
            high = pivot;
        } else if (numbers[pivot] > numbers[high]) {
            low = pivot + 1;
        } else {
            high -= 1;
        }
    }
    return numbers[low];
};

12. 矩阵中的路径

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

例如，在下面的 3×4 的矩阵中包含单词 “ABCCED”（单词中的字母已标出）。

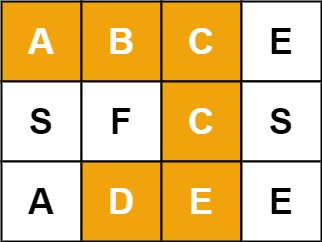
示例 1：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2：

输入：board = [["a","b"],["c","d"]], word = "abcd"
输出：false

提示：

• 1 <= board.length <= 200
• 1 <= board[i].length <= 200
• board 和 word 仅由大小写英文字母组成

题目地址：https://leetcode-cn.com/problems/ju-zhen-zhong-de-lu-jing-lcof/

解题思路

DFS + 剪枝

DFS：深度搜索二叉树
剪枝：遇到不符合条件的情况，提前返回，即答案中代码的

// 如果越界(行或列) 或 匹配到的字符与 word 当前遍历到的下标不同，直接返回
if ([-1, board.length].includes(i) || [-1, board[0].length].includes(j) || board[i][j] !== word[k]) 
    return false;

DFS 解析：

• 递归参数： 当前元素在矩阵 board 中的行列索引 i 和 j ，当前目标字符在 word 中的索引 k 。
• 终止条件：
  • 返回 false：
    • 行或列索引越界
    • 当前矩阵元素与目标字符不同
    • 当前矩阵元素已访问过（通过将访问过的字符置空）
  • 返回 true： k = word.length - 1 ，即字符串 word 已全部匹配。
• 递推过程：
  • 标记当前矩阵元素： 将 board[i][j] 修改为 空字符 ‘’ ，代表此元素已访问过，防止之后搜索时重复访问。
  • 搜索下一单元格： 朝当前元素的 上、下、左、右 四个方向开启下层递归，使用 或 连接 （代表只需找到一条可行路径就直接返回，不再做后续 DFS ），并记录结果至 res 。
  • 还原当前矩阵元素： 将 board[i][j] 元素还原至初始值，即 word[k] 。
  • 返回值： 返回布尔量 res ，代表是否搜索到目标字符串。

/**
 * @param {character[][]} board
 * @param {string} word
 * @return {boolean}
 */
var exist = function(board, word) {
    const dfs = (i, j, k) => {
        // 如果长度一样了，说明找到该路径了
        if (k === word.length) return true;
        // 如果越界(行或列) 或 匹配到的字符与 word 当前遍历到的下标不同，直接返回
        if ([-1, board.length].includes(i) || [-1, board[0].length].includes(j) || board[i][j] !== word[k]) return false;
        // 置空表明已经遍历过该字符了
        board[i][j] = null;
        // 在置空表明已经遍历过该字符了的前提下，继续递归上下右左看是否有满足等于单词的路径，只要有一个路径满足就行，所以 || 连接
        const res = dfs(i + 1, j, k + 1) || dfs(i, j + 1, k + 1) || dfs(i - 1, j, k + 1) || dfs(i, j - 1, k + 1);
        // 上面递归完后，要将字符变回来，复原现场，毕竟两层 for 循环每次都要用到 board 数组
        board[i][j] = word[k];
        return res;
    }
    for(let i = 0; i < board.length; i++) {
        for(let j = 0; j < board[0].length; j++) {
            if (dfs(i, j, 0)) return true;
        }
    }
    return false;
};

17. 打印从1到最大的n位数

输入数字 n，按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3，则打印出 1、2、3 一直到最大的 3 位数 999。

示例 1:

输入: n = 1
输出: [1,2,3,4,5,6,7,8,9]

说明：

• 用返回一个整数列表来代替打印
• n 为正整数

题目地址：https://leetcode-cn.com/problems/da-yin-cong-1dao-zui-da-de-nwei-shu-lcof/

解题思路

1. 根据n确定要打印的最大值，如果n是3，那maxNum就是10 * 10 * 10 - 1，也就是说10 乘上3次
2. 循环从1到最大值，左闭右闭区间，里面的数字加入结果集中

/**
 * @param {number} n
 * @return {number[]}
 */
var printNumbers = function(n) {
    if (n <= 0) return [];
    let num = 1;
    let res = [];
    for (let i = 0; i < n; i++) num *= 10;
    for (let i = 1; i < num; i++) res.push(i);
    return res;
};

21. 调整数组顺序使奇数位于偶数前面

输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有奇数在数组的前半部分，所有偶数在数组的后半部分。

示例：

输入：nums = [1,2,3,4]
输出：[1,3,2,4] 
注：[3,1,2,4] 也是正确的答案之一。

提示：

1. 0 <= nums.length <= 50000
2. 0 <= nums[i] <= 10000

题目地址：https://leetcode-cn.com/problems/diao-zheng-shu-zu-shun-xu-shi-qi-shu-wei-yu-ou-shu-qian-mian-lcof/

解题思路

考虑定义双指针 i , j 分列数组左右两端，循环执行：

1. 指针 i 从左向右寻找偶数；
2. 指针 j 从右向左寻找奇数；
3. 将 偶数 nums[i] 和 奇数 nums[j]交换。

可始终保证： 指针 i 左边都是奇数，指针 j 右边都是偶数 。

/**
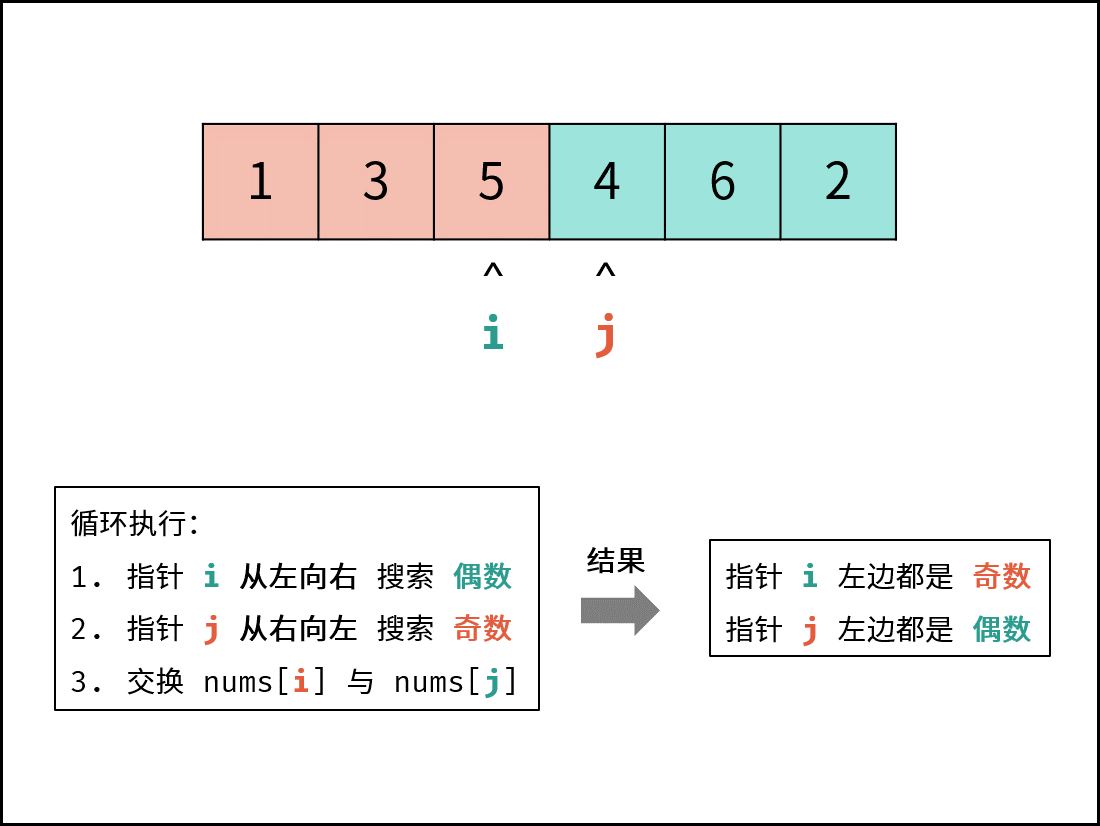
 * @param {number[]} nums
 * @return {number[]}
 */
var exchange = function(nums) {
    let [i, j] = [0, nums.length - 1];
    while(i < j) {
        while(i < j && nums[i] % 2 === 1) i++;
        while(i < j && nums[j] % 2 === 0) j--;
        [nums[i], nums[j]] = [nums[j], nums[i]];
    }
    return nums;
};

29. 顺时针打印矩阵

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

限制：

• 0 <= matrix.length <= 100
• 0 <= matrix[i].length <= 100

题目地址：https://leetcode-cn.com/problems/shun-shi-zhen-da-yin-ju-zhen-lcof/

解题思路

考虑设定矩阵的“左、上、右、下”四个边界，模拟以上矩阵遍历顺序。

/**
 * @param {number[][]} matrix
 * @return {number[]}
 */
var spiralOrder = function(matrix) {
    if (!matrix.length) return [];
    const result = [];
    let [l, r, t, b] = [0, matrix[0].length - 1, 0, matrix.length - 1];
    while(1) {
        for(let i = l; i <= r; i++) {
            result.push(matrix[t][i]);
        }
        t++;
        if (t > b) break;
        for(let i = t; i <= b; i++) {
            result.push(matrix[i][r]);
        }
        r--;
        if (l > r) break;
        for(let i = r; i >= l; i--) {
            result.push(matrix[b][i]);
        }
        b--;
        if (t > b) break;
        for(let i = b; i >= t; i--) {
            result.push(matrix[i][l]);
        }
        l++;
        if (l > r) break;
    }
    return result;
};

31. 栈的压入、弹出序列

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如，序列 {1,2,3,4,5} 是某栈的压栈序列，序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列，但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。

示例 1：

输入：pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出：true
解释：我们可以按以下顺序执行：
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1

示例 2：

输入：pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出：false
解释：1 不能在 2 之前弹出。

提示：

• 0 <= pushed.length == popped.length <= 1000
• 0 <= pushed[i], popped[i] < 1000
• pushed 是 popped 的排列。

题目地址：https://leetcode-cn.com/problems/zhan-de-ya-ru-dan-chu-xu-lie-lcof/

解题思路

1. 按照入栈序列的顺序压栈
2. 每次压栈之后，循环判断 “栈顶元素 = 弹出序列的当前元素” 是否成立，将符合弹出序列顺序的栈顶元素全部弹出
3. 最后如果栈为空则满足条件，否则不满足

/**
 * @param {number[]} pushed
 * @param {number[]} popped
 * @return {boolean}
 */
var validateStackSequences = function(pushed, popped) {
    let index = 0;
    const stack = [];
    for(const value of pushed) {
        stack.push(value);
        while(stack.length && stack[stack.length - 1] === popped[index]) {
            stack.pop();
            index ++;
        }
    }
    return stack.length === 0;
};

39. 数组中出现次数超过一半的数字

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1:

输入: [1, 2, 3, 2, 2, 2, 5, 4, 2]
输出: 2

限制：

• 1 <= 数组长度 <= 50000

题目地址：https://leetcode-cn.com/problems/shu-zu-zhong-chu-xian-ci-shu-chao-guo-yi-ban-de-shu-zi-lcof/

解题思路

方法一：数组排序法

将数组 nums 排序，数组中点的元素 一定为众数。

/**
 * @param {number[]} nums
 * @return {number}
 */
var majorityElement = function(nums) {
    nums.sort();
    return nums[Math.floor(nums.length / 2)];
};

方法二：哈希表统计法

遍历数组 nums ，用 HashMap 统计各数字的数量，即可找出 众数 。

/**
 * @param {number[]} nums
 * @return {number}
 */
var majorityElement = function(nums) {
    if (nums.length === 1) return nums[0];
    const count = {};
    const target = nums.length / 2;
    for(const v of nums) {
        if (v in count) {
            count[v] ++;
            if (count[v] > target) return v;
        } else {
            count[v] = 1;
        }
    }
    
};

方法三：摩尔投票法

设输入数组 nums 的众数为 x，数组长度为 n。

推论一： 若记 众数 的票数为 +1 ，非众数 的票数为 -1 ，则一定有所有数字的 票数和 >0 。

推论二： 若数组的前 a 个数字的 票数和 = 0 ，则 数组剩余 (n−a) 个数字的 票数和一定仍 > 0 ，即后 (n−a) 个数字的 众数仍为 x 。

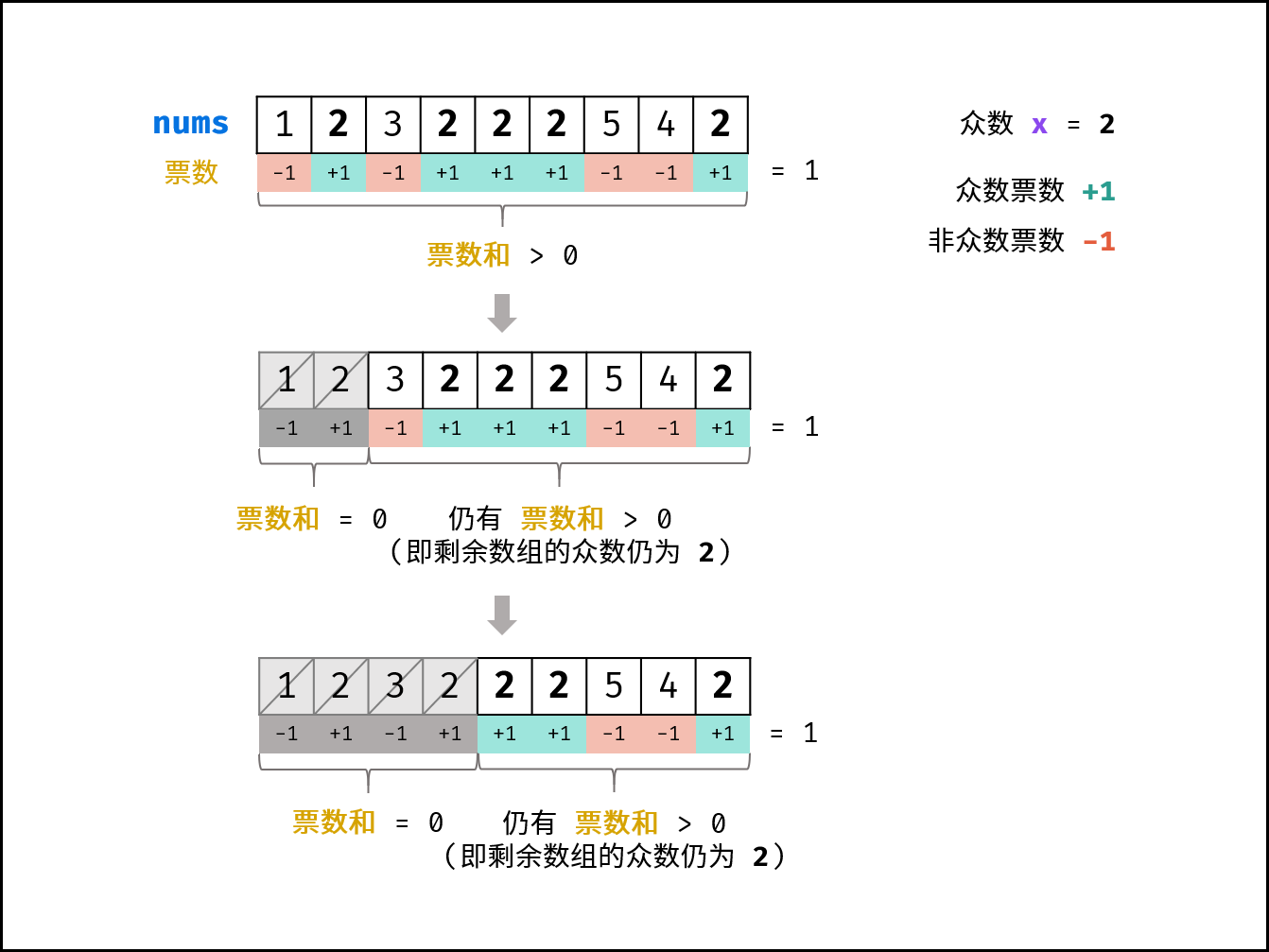
根据以上推论，记数组首个元素为 n1 ，众数为 x ，遍历并统计票数。当发生 票数和 = 0 时，剩余数组的众数一定不变 ，这是由于：

• 当 n1 = x ： 抵消的所有数字中，有一半是众数 x 。
• 当 n1 = x ： 抵消的所有数字中，众数 x 的数量最少为 0 个，最多为一半。

利用此特性，每轮假设发生 票数和 = 0 都可以 缩小剩余数组区间 。当遍历完成时，最后一轮假设的数字即为众数。

/**
 * @param {number[]} nums
 * @return {number}
 */
var majorityElement = function(nums) {
    let votes = 0, x;
    for(const v of nums) {
        if(votes === 0) x = v;
        votes += (x === v ? 1 : -1);
    }
    return x;
};

40. 最小的k个数

输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。

示例 1：

输入：arr = [3,2,1], k = 2
输出：[1,2] 或者 [2,1]

示例 2：

输入：arr = [0,1,2,1], k = 1
输出：[0]

限制：

• 0 <= k <= arr.length <= 10000
• 0 <= arr[i] <= 10000

题目地址：https://leetcode-cn.com/problems/zui-xiao-de-kge-shu-lcof/

解题思路

对原数组从小到大排序后取出前 kk 个数即可。

/**
 * @param {number[]} arr
 * @param {number} k
 * @return {number[]}
 */
var getLeastNumbers = function(arr, k) {
    if (arr.length <= k) return arr;
    arr.sort((a, b) => a - b);
    return arr.slice(0, k);
};

42. 连续子数组的最大和

输入一个整型数组，数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。

要求时间复杂度为O(n)。

示例1:

输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

提示：

• 1 <= arr.length <= 10^5
• -100 <= arr[i] <= 100

题目地址：https://leetcode-cn.com/problems/lian-xu-zi-shu-zu-de-zui-da-he-lcof/

解题思路

动态规划

对于 [B, A, C] 连续三个数

什么是负贡献？
对于新的数A假设是10，如果前面的一个数B是-2，那么前面的B就会对新的A产生了负贡献，让他变成了8，那么就舍弃加B，直接重新从A开始加起，因为此时是最大的

什么是正贡献？
对于新的数C假设是5，如果前面的一个数A是10，那么前面的A就会对新的C产生了正贡献，让他变成了15，所以就要加埋C，此时和15会比原本的A更大

理清楚正贡献与负贡献后，下面开始该题的讲解：

记录第n位连续数组最大和时，先判断前一位记录的最大和是正的还是负的

• 如果是负的，那加上新加这个数，肯定会比新加这个数要小，即对新的数产生了负贡献，那么就不要加这个负的前一位记录的最大和，直接使用新的数作为数组初始位即可
• 如果是正的，那么是正贡献，加上新的数肯定会比新的数要大，可以赋值

/**
 * @param {number[]} nums
 * @return {number}
 */
var maxSubArray = function(nums) {
    let pre = nums[0], result = nums[0];
    for(let i = 1; i < nums.length; i++) {
        // 前面的 连续数组和是负数，做出的是负贡献，如果是正数，做出的是正贡献，才进行连续赋值
        if (pre > 0) {
            pre = pre + nums[i];
        } else {
            pre = nums[i];
        }
        result = Math.max(result, pre);
    }
    return result;
};

47. 礼物的最大价值

在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

示例 1:

输入: 
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物

提示：

• 0 < grid.length <= 200
• 0 < grid[0].length <= 200

题目地址：https://leetcode-cn.com/problems/li-wu-de-zui-da-jie-zhi-lcof/

解题思路

根据题目说明，易得某单元格只可能从上边单元格或左边单元格到达。

设 f(i,j) 为从棋盘左上角走至单元格 (i,j) 的礼物最大累计价值，易得到以下递推关系：f(i,j) 等于 f(i,j−1) 和 f(i−1,j) 中的较大值加上当前单元格礼物价值 grid(i,j) 。

因此，可用动态规划解决此问题。

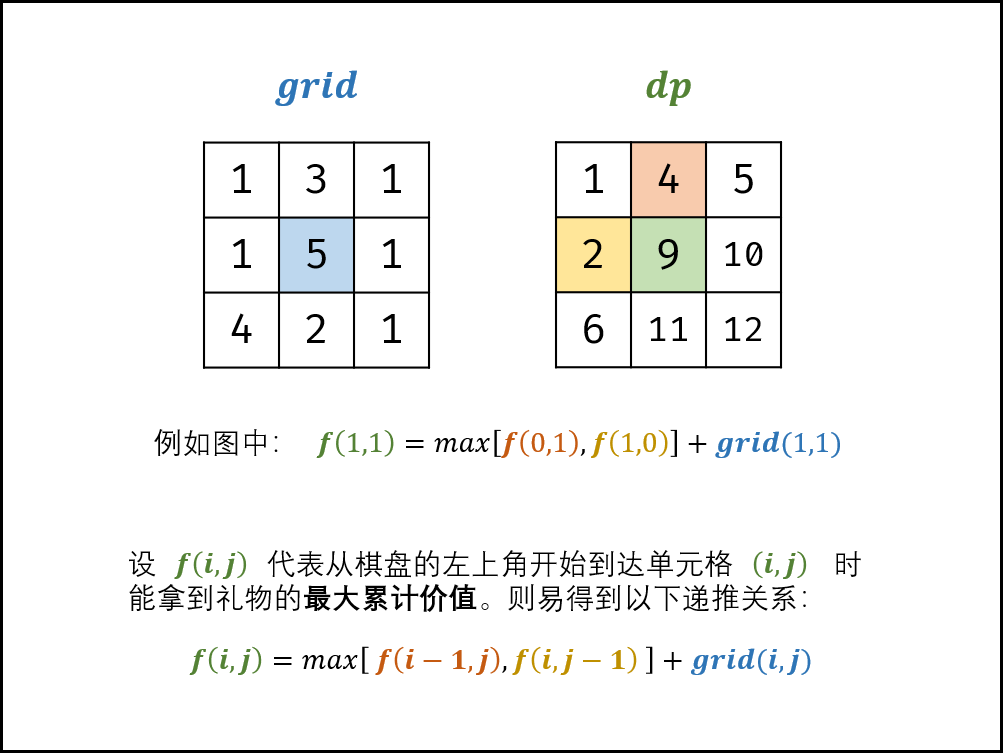
动态规划解析：

• 状态定义： 设动态规划矩阵 dp ，dp(i,j) 代表从棋盘的左上角开始，到达单元格 (i,j) 时能拿到礼物的最大累计价值。
• 转移方程：
  1. 当 i = 0 且 j = 0 时，为起始元素；
  2. 当 i = 0 且 j != 0 时，为矩阵第一行元素，只可从左边到达；
  3. 当 i != 0 且 j = 0 时，为矩阵第一列元素，只可从上边到达；
  4. 当 i != 0 且 j != 0 时，为矩阵第一列元素，只可从上边到达；
• 初始状态： dp[0][0] = grid[0][0] ，即到达单元格 (0,0) 时能拿到礼物的最大累计价值为 grid[0][0] ；
• 返回值： dp[m-1][n-1] ，m, n 分别为矩阵的行高和列宽，即返回 dp 矩阵右下角元素。

空间复杂度优化：

• 由于 dp[i][j]只与 dp[i-1][j] , dp[i][j-1] , grid[i][j]有关系，因此可以将原矩阵 grid 用作 dp 矩阵，即直接在 grid 上修改即可。
• 应用此方法可省去 dp 矩阵使用的额外空间，因此空间复杂度从 O(MN) 降至 O(1) 。

/**
 * @param {number[][]} grid
 * @return {number}
 */
var maxValue = function(grid) {
    for(let i = 0; i < grid.length; i++) {
        for(let j = 0; j < grid[0].length; j++) {
            if(i === 0 && j === 0) continue;
            if(i === 0) grid[i][j] += grid[i][j - 1];
            else if (j === 0) grid[i][j] += grid[i - 1][j];
            else grid[i][j] += Math.max(grid[i - 1][j], grid[i][j - 1]);
        }
    }
    return grid[grid.length - 1][grid[0].length - 1];
};

以上代码逻辑清晰，和转移方程直接对应，但仍可提升效率：当 grid 矩阵很大时， i = 0 或 j = 0 的情况仅占极少数，相当循环每轮都冗余了一次判断。因此，可先初始化矩阵第一行和第一列，再开始遍历递推。

/**
 * @param {number[][]} grid
 * @return {number}
 */
var maxValue = function(grid) {
    for(let i = 1; i < grid.length; i++) grid[i][0] += grid[i - 1][0];
    for(let j = 1; j < grid[0].length; j++) grid[0][j] += grid[0][j - 1];
    for(let i = 1; i < grid.length; i++) {
        for(let j = 1; j < grid[0].length; j++) {
           grid[i][j] += Math.max(grid[i - 1][j], grid[i][j - 1]);
        }
    }
    return grid[grid.length - 1][grid[0].length - 1];
};